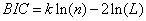AIC, BIC v.s. Crossvalidation

2024-02-27 07:08

文章标签 bic aic crossvalidation

本文主要是介绍AIC, BIC v.s. Crossvalidation，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

模型选择的方法有许多，例如 AIC, BIC, Crossvalidation, GCV等等。这

些准则的适用条件有哪些？该如何选择不同的准则？

AIC, BIC准则

ref：https://methodology.psu.edu/node/504
ref：https://en.wikipedia.org/wiki/Bayesian_information_criterion
ref：https://en.wikipedia.org/wiki/Akaike_information_criterion

AIC和BIC均是基于似然函数的准则：

- 2 log L + k p

$-2\log L+kp$
其中

L $L$ 是似然函数,

p $p$ 是模型参数的个数。

AIC: $k=2$
AIC目标：估计量与真实值的Kullback–Leibler距离达到最小，同时，控制过拟合（overfitting）

BIC: k=logn

这篇关于AIC, BIC v.s. Crossvalidation的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

http://www.chinasem.cn/article/751576。 23002807@qq.com

压缩感知与Nquist抽样定理——模拟信息转换(AIC)学习总结

原文链接：http://blog.csdn.net/jbb0523/article/details/41595535 一、引言压缩感知（CompressiveSensing, or Compressed Sensing）或译为压缩传感，或者称为压缩采样（Compressive sampling），以下统称压缩感知，简称CS。在压缩感知的有关文献中几乎都在说“压缩感知突破了传统的Nq

k-折交叉验证(k-fold CrossValidation)

在机器学习中，将数据集A分为训练集（training set）B和测试集（test set）C，在样本量不充足的情况下，为了充分利用数据集对算法效果进行测试，将数据集A随机分为k个包，每次将其中一个包作为测试集，剩下k-1个包作为训练集进行训练。在matlab中，可以利用： indices=crossvalind('Kfold',x,k); 来实现随机分包的操作，其

COMSOL光学模型：等离激元BIC非偏振结构

COMSOL光学模型：等离激元BIC非偏振结构在光学领域中，研究等离子激元（plasmon）的激发和调控一直备受关注。等离子激元是电磁波与金属纳米结构相互作用的一种现象，具有局域电磁场增强和局域化光学特性。在等离子激元领域，科学家们一直致力于寻找一种有效控制等离子激元耦合和调控的方法，其中，等离子激元的束缚态共振（bound states in the continuum, BIC）是一种

压缩感知与Nquist抽样定理——模拟信息转换(AIC)学习总结

论文阅读 - BIC: Twitter Bot Detection with Text-Graph Interaction and Semantic Consistency

论文链接：https://arxiv.org/abs/2208.08320 目录 1 摘要 2 绪论 3 相关工作 3.1 Twitter-bot Detection 3.2 Text-Graph Interaction 4 问题定义 5 方法 5.1 模态交互 5.2 语义一致性检测 5.3 训练和推理 6 实验 6.1 实验设置 6.2 实验结果 6.3

bic谈话_让谈话强化学习基础知识第二部分

bic谈话 This is a continuation of the article Let’s talk Reinforcement Learning — The Fundamentals — Part 1. You can continue reading this article even if you have not read Part 1 if you can recogn

aic值检验 p值_参数估计和假设检验

前言：所谓统计推断，就是利用样本所提供的信息对总体的某些统计特征进行估计或者判断，进而认识总体。统计推断分为两大类：参数估计，假设检验。 1 .参数估计参数估计和假设检验是统计推断的基本内容，几乎所有统计建模的PROC步都会设计参数估计以及相对应的假设检验。假设总体的分布函数的类型已知，但其中一个或者多个参数未知，那么就需要对这些未知的参数做出合理的估计，并且对估计做出评价，这

AIC 和 BIC

此处模型选择我们只考虑模型参数数量，不涉及模型结构的选择。很多参数估计问题均采用似然函数作为目标函数，当训练数据足够多时，可以不断提高模型精度，但是以提高模型复杂度为代价的，同时带来一个机器学习中非常普遍的问题——过拟合。所以，模型选择问题在模型复杂度与模型对数据集描述能力（即似然函数）之间寻求最佳平衡。人们提出许多信息准则，通过加入模型复杂度的惩罚项来避免过拟合问题，此处我们介绍一下常用

R语言逐步回归分析 AIC

关注微信公共号：小程在线关注CSDN博客：程志伟的博客逐步回归分析是以AIC信息统计量为准则，通过选择最小的AIC信息统计量，来达到删除或增加变量的目的。 R语言中用于逐步回归分析的函数 step() drop1() add1() #1.载入数据首先对数据进行多元线性回归分析 tdata<-data.frame(x1=c( 7, 1,11,11,

#PCIE# PCIe的接口形态之Add-in-Card(AIC)

PCIe AIC 是最常见的PCIe接口形态，组装过电脑的同学可能比较清楚，电脑上的主板上都会有下面的几排插槽，这就是典型的PCIe AIC的插槽，比较常见的插槽位宽为x16和x1 链接自https://www.muycomputerpro.com/2019/06/01/pci-express-5-0 插在上面的卡就是PCIe AIC。PCIe AIC常见的有显卡，无线网卡，存储设备等等

AIC, BIC v.s. Crossvalidation

相关文章