本文主要是介绍集成算法(装袋,随机森林,boosting),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
集成学习定义
将多个单个学习器集成在一起,使它们共同完成学习任务,已达到提高预测准确率的目的,也称“多分类器系统”
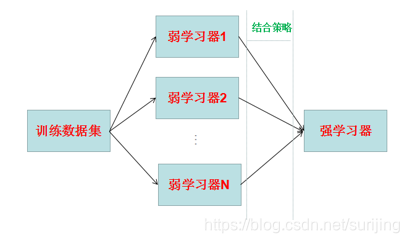
例:做练习题的时候题目的准确率不高,通过多个学生的答案进行核对,提高题目的准确率
分两大类:
| 装袋 | bagging,随机森林 |
|---|---|
| 提升 | boosting,adaboost,GBDT,XGBoot |
集成学习一般过程
- 令D表示原始训练数据集,k表示基分类器 (基学习器)的个数,Z表示测试数据集。
- for i=1 to k do 由D创建训练集Di 由Di创建基分类器Ci
- end for
- for 每一个测试样本do
C*(x)=Vote(C1(x),C2(x),…,Ck(x)) end for
如何对学习结果进行结合
| 投票法 | 对于分类问题的预测。 |
|---|---|
| 平均法 | 对于数值类的回归预测。分为:平均法和加权平均法 |
| 学习法 | 为了解决投票法和平均法误差较大的问题。在弱学习器之后再加一层学习器 |
集成方法:
- 一种是使用训练集的不同子集训练得到不同的基分类器。(bagging)
- 另一种方法是使用同一个训练集的不同属性子集训练得到不同的基分类器。(随机森林)
Bagging:
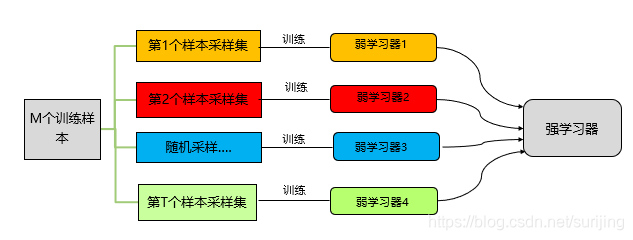
对训练集有放回地抽取训练样例,从而为每一个基本学习器都构造出一个与训练集相当大小但各不相同的训练集,从而训练出不同的基本学习器;该算法是基于对训练集进行处理的集成方法中最简单、最直观的一种。
算法流程:
1.从大小为n的原始数据集D中独立随机地抽取n’个数据(n’<=n),形成一个自助数据集;
- 重复上述过程,产生出K个独立的自助数据集;
- 利用K个自助数据集训练出k个最优模型;
- 分类问题:最终的分类结果由这k个最优模型各自的判别结果投票决定;回归问题:对K个模型的值求平均得到最终结果。
- 另外由于每一个样本被选中的概率相同,因此装袋并不侧重于训练数据集中的任何特定实例。因此对于噪声数据&#x
这篇关于集成算法(装袋,随机森林,boosting)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






