本文主要是介绍[深度学习]Part2 K临近算法(KNN)Ch02——【DeepBlue学习笔记】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
本文仅供学习使用
K临近算法(KNN)Ch02
- 1. KNN算法原理
- 1.1 案例分析
- 1.2 KNN三要素
- 1.3 KNN分类预测规则
- 1.4 KNN回归预测规则
- 2. KNN算法法实现方式
- 2.1 KD Tree
- 2.1.1 KD Tree构建方式
- 2.1.1 KD tree查找最近邻
- 2.2 KNN参数说明
- 3. KNN代码
- 3.1 KNN参等权分类
- 3.2 KNN加权分类
- 3.3 KNN训练
- 3.4 调用sklearn
- 4. 补充
1. KNN算法原理
K近邻(K-nearst neighbors, KNN)是一种基本的机器学习算法,所谓 k 近邻,就是 k 个最近的邻居的意思,说的是每个样本都可以用它最接近的 k个邻居来代表。比如:判断一个人的人品,只需要观察与他来往最密切的几个人的人品好坏就可以得出,即“近朱者赤,近墨者黑”;KNN算法既可以应用于分类应用中,也可以应用在回归应用中。
• KNN在做回归和分类的主要区别在于最后做预测的时候的决策方式不同。
KNN在分类预测时,一般采用多数表决法;而在做回归预测时,一般采用平均值法。
- 从训练集合中获取K个离待预测样本距离最近的样本数据;
- 根据获取得到的K个样本数据来预测当前待预测样本的目标属性值。
1.1 案例分析
我们标记电影的类型:爱情片,动作片 ;每个电影有两个特征属性:打斗镜头,接吻镜头; 预测一个新的电影的电影类型:
-
将训练集中的所有样例画入坐标系,也将待测样例画入

-
计算待测分类的电影与所有已知分类的电影的欧式距离

-
将这些电影按照距离升序排序,取前k个电影,假设k=3,那么我们得到的电影依次是《He’s Not Really Into Dudes》、《Beautiful Woman》和《California Man》。而这三部电影全是爱情片,因此我们判定未知电影是爱情片。
1.2 KNN三要素
在KNN算法中,非常重要的主要是三个因素:
• K值的选择:
对于K值的选择,一般根据样本分布选择一个较小的值,然后通过交叉验证来选择一个比较合适的最终值;当选择比较小的K值的时候,表示使用较小领域中的样本进行预测,训练误差会减小,但是会导致模型变得复杂,容易过拟合;当选择较大的K值的时候,表示使用较大领域中的样本进行预测,训练误差会增大,同时会使模型变得简单,容易导致欠拟合;
• 距离的度量:
一般使用欧氏距离(欧几里得距离);
闵可夫斯基距离(Minkowski Distance): L ( x ( i ) , x ( j ) ) = ( ∑ k = 1 n ∣ x k ( i ) − x k ( j ) ∣ p ) 1 p L({{x}^{(i)}},{{x}^{(j)}})={{\left( \sum\limits_{k=1}^{n}{{{\left| x_{k}^{(i)}-x_{k}^{(j)} \right|}^{p}}} \right)}^{\frac{1}{p}}} L(x(i),x(j))=(k=1∑n∣ ∣xk(i)−xk(j)∣ ∣p)p1,当 p = 2 p=2 p=2 时,即为欧氏距离
• 决策规则:
在分类模型中,主要使用多数表决法或者加权多数表决法;在回归模型中,主要使用平均值法或者加权平均值法。
而在两种方法中都需要考虑阈值(分界点)的设定
1.3 KNN分类预测规则
在KNN分类应用中,一般采用多数表决法或者加权多数表决法。
• 多数表决法:
每个邻近样本的权重是一样的,也就是说最终预测的结果为出现类别最多的那个类,比如图中最终类别为圆圈;
• 加权多数表决法:
每个邻近样本的权重是不一样的,一般情况下采用权重和距离成反比的方式来计算,也就是说最终预测结果是出现权重最大的那个类别;比如右图中,假设三个红色点到待预测样本点的距离均为2,两个黄色点到待预测样本点距离为1,那么最终类别为星号。

1.4 KNN回归预测规则
在KNN回归应用中,一般采用平均值法或者加权平均值法。
• 平均值法:
每个邻近样本的权重是一样的,也就是说最终预测的结果为所有邻近样本的目标属性值的均值;比如图中,蓝色圆圈的最终预测值为:2.6;
• 加权平均值法:
每个邻近样本的权重是不一样的,一般情况下采用权重和距离成反比的方式来计算,也就是说在计算均值的时候进行加权操作;比如图中,假设上面三个点到待预测样本点的距离均为2,下面两个点到待预测样本点距离为1,那么蓝色圆圈的最终预测值为:2.43。(权重分别为: 1/7和2/7)

2. KNN算法法实现方式
KNN算法的重点在于找出K个最邻近的点,主要方式有以下几种:
• 蛮力实现(brute): 计算预测样本到所有训练集样本的距离,然后选择最小的k个距离即可得到K个最邻近点。缺点在于当特征数比较多、样本数比较多的时候,算法的执行效率比较低;
• KD树(kd_tree): KD树算法中,首先是对训练数据进行建模,构建KD树,然后再根据建好的模型来获取邻近样本数据。
除此之外,还有一些从KD_Tree修改后的求解最邻近点的算法, 比如:Ball Tree、BBF Tree、MVP Tree等。
2.1 KD Tree
KD Tree是KNN算法中用于计算最近邻的快速、便捷构建方式。
当样本数据量少的时候,我们可以使用 brute 这种暴力的方式行求解最近邻,即计算到所有样本的距离。但是当样本量比较大的时候,直接计算所有样本的距离,工作量有点大,所以在这种情况下,我们可以使用kd tree来快速的计算。
2.1.1 KD Tree构建方式
KD树采用从m个样本的n维特征中,分别计算n个特征取值的方差,用方差最大的第k维特征nk作为根节点。对于这个特征,选择取值的中位数nkv作为样本的划分点,对于小于该值的样本划分到左子树,对于大于等于该值的样本划分到右子树,对左右子树采用同样的方式找方差最大的特征作为根节点,递归即可产生 KD树。

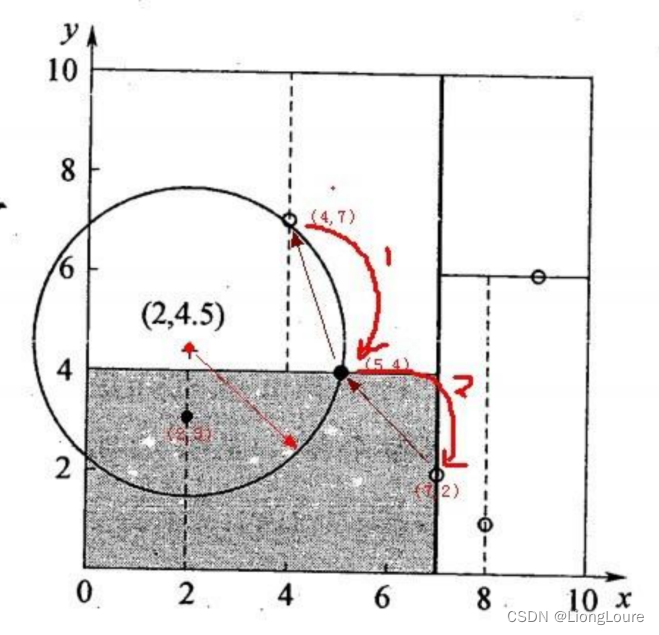
二维样本: {(2,3), (5,4), (9,6), (4,7), (8,1), (7,2)}
- 选择x(1)轴,6个数据点的x(1)坐标上的数字分别是2,5,9,4,8,7。取中位数7(不是严格意义的中位数,取较大的数),以x(1)=7将特征空间分为两个矩形:
- 选择x(2)轴,处理左子树,3个数据点的x(2)坐标上的数字 分别是3,4,7。取中位数4,以x(2)=4将左子树对应的特征空间分 为两个矩形;处理右子树,2个数据点的x(2)坐标上的数字分别是 6,1。取6,以x(2)=6将右子树对应的特征空间分为两个矩形:
- x(1)轴,分别处理所有待处理的节点:
2.1.1 KD tree查找最近邻
当我们生成KD树以后,就可以去预测测试集里面的样本目标点了。对于一个目标点,我们首先在KD树里面找到包含目标点的叶子节点。以目标点为圆心,以目标点到叶子节点中样本实例的最短距离为半径,得到一个超球体,最近邻的点一定在这个超球体内部。然后返回子节点的父节点,检查另一个子节点包含的超矩形体是否和超球体相交,如果相交就到这个子节点寻找是否有更加近的近邻,有的话就更新最近邻。如果不相交那就简单了,我们直接返回父节点的父节点,在另一个子树继续搜索最近邻。当回溯到根节点时,算法结束,此时保存的最近邻节点就是最终的最近邻。
找到所属的叶子节点后,以目标点为圆心,以目标点到最近样本点(一般为当前叶子节点中的其它训练数据或者刚刚经过的父节点) 为半径画圆,从最近样本点往根节点进行遍历,如果这个圆和分割节点的分割线有交线,那么就考虑分割点的另外一个子树。如果在遍历过程中,找到距离比刚开始的样本距离近的样本,那就进行更新操作。
一直迭代遍历到根节点上,结束循环找到最终的最小距离的样本。
2.2 KNN参数说明
| 参数 | KNeighborsClassifier —————— KNeighborsRegressor |
|---|---|
| weights | 样本权重,可选参数: uniform(等权重)、distance(权重和距离成反比,越近影响越强);默认为uniform |
| n_neighbors | 邻近数目,默认为5 |
| algorithm | 计算方式,默认为auto,可选参数: auto、ball_tree、kd_tree、brute;推荐选择kd_tree |
| leaf_size | 在使用KD_Tree、Ball_Tree的时候,允许存在最多的叶子数量,默认为30 |
| metric | 样本之间距离度量公式,默认为minkowski(闵可夫斯基);当参数p为2的时候,其实就是欧几里得距离 |
| p | 给定minkowski距离中的p值,默认为2 |
3. KNN代码
3.1 KNN参等权分类
'''
等权分类
'''
import numpy as np
import pandas as pd##初始化训练数据
T = [[3, 104, -1],[2, 100, -1],[1, 81, -1],[101, 10, 1],[99, 5, 1],[98, 2, 1]]
##预测数据
x_test = [18, 90]
##邻居
K = 5
###列表 [[dis1,标签1],[dis2,标签2].。。。。。。]
listdistance = []
##循环每一个数据,计算他的dis
for t in T: ## t是每条电影的数据dis = np.sum((np.array(t[:-1]) - np.array(x_test)) ** 2) ** 0.5listdistance.append([dis, t[-1]])
# print(listdistance)
##按照dis进行排序
listdistance.sort()print(listdistance)
##选取K个邻居放入投票箱
# print(listdistance[:K])
arr = np.array(listdistance[:K])[:, -1]
print(arr)
##统计投票
a = pd.Series(arr).value_counts()
print(a)
pre = a.idxmax() # idxmax
print(pre)
3.2 KNN加权分类
import numpy as np# ## KNN加权投票--分类
# #初始化数据
T = [[3, 104, -1],[2, 100, -1],[1, 81, -1],[101, 10, 1],[99, 5, 1],[98, 2, 1]]
# #初始化待测样本
x = [18, 90]
# x = [3,104]
# x = [50, 50]
# #初始化邻居数
K = 3
# #初始化存储距离列表[[距离1,标签1],[距离2,标签2]....]
listDistance = []
# #循环每一个数据点,把计算结果放入dis
for i in T:dis = np.sum((np.array(i[:-1]) - np.array(x)) ** 2) ** 0.5 ##欧氏距离listDistance.append([dis, i[-1]])
# #对dis按照距离排序
listDistance.sort()print(listDistance)
weight = [1/i[0] for i in listDistance[:K]]
print(weight)
weight /= sum(weight)
print(weight)pre = -1 if sum([1 / i[0] * i[1] for i in listDistance[:K]]) < 0 else 1
print(pre)
3.3 KNN训练
'''
简单实现一下等权分类 封装成KNN类实现fit,predict,score方法'''
import numpy as np
import pandas as pdclass KNN:'''KNN的步骤:1、从训练集合中获取K个离待预测样本距离最近的样本数据;2、根据获取得到的K个样本数据来预测当前待预测样本的目标属性值'''def __init__(self, k):self.k = kpassdef fit(self, x, y):'''训练模型 实际上就是存储数据:param x: 训练数据x:param y: 训练数据y:return:'''### 将数据转化为numpy数组的形式进行存储self.train_x = np.array(x)self.train_y = np.array(y)def feach_k_neighbors(self, x):'''# 1、从训练集合中获取K个离待预测样本距离最近的样本数据;# 2、根据获取得到的K个样本数据来预测当前待预测样本的目标属性值:param x:待预测的一条数据:return: 最近k个邻居的label'''###列表 [[dis1,标签1],[dis2,标签2].。。。。。。]listdistance = []##循环每一个数据,计算他的disfor index, i in enumerate(self.train_x): ## t是每条电影的数据# print(index)dis = np.sum((np.array(i) - np.array(x)) ** 2) ** 0.5listdistance.append([dis, self.train_y[index]])# print(listdistance)##按照dis进行排序listdistance.sort()# print(listdistance)# sys.exit()##选取K个邻居放入投票箱# print(listdistance[:self.k])arr = np.array(listdistance[:self.k])[:, -1]# print(arr)return arrdef predict(self, x):'''对待预测数据进行预测:param x: 待预测数据的特征属性 x 是个矩阵:return: 所有数据的预测label'''### 将数据转化为numpy数组的形式self.pre_x = np.array(x)# 遍历每一条带预测数据Y_pre = []for x in self.pre_x:# print(x)# 1、从训练集合中获取K个离待预测样本距离最近的样本数据;k_nearst_neighbors_label = self.feach_k_neighbors(x)# 2、根据获取得到的K个样本数据来预测当前待预测样本的目标属性值##统计投票a = pd.Series(k_nearst_neighbors_label).value_counts()# print(a)# pre = a.idxmax() ##idxmax() 和 argmax 功能一样,获取最大值对应的下标索引y_pre = a.idxmax()# pre = a.argmax()# print(pre)Y_pre.append(y_pre)return Y_predef score(self, x, y):''':param x::param y::return: 准确率'''y_hat = self.predict(x)acc = np.mean(y == y_hat)return accif __name__ == '__main__':T = np.array([[3, 104, -1],[2, 100, -1],[1, 81, -1],[101, 10, 1],[99, 5, 1],[98, 2, 1]])X_train = T[:, :-1]Y_train = T[:, -1]x_test = [[18, 90], [50, 50]]knn = KNN(k=5)knn.fit(x=X_train, y=Y_train)print(knn.predict(X_train))print(knn.predict(x_test))print(knn.score(x=X_train, y=Y_train))# knn.fetch_k_neighbors(x_test[0])print('预测结果:{}'.format(knn.predict(x_test)))print('-----------下面测试一下鸢尾花数据-----------')from sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_splitX, Y = load_iris(return_X_y=True)print(X.shape, Y.shape)x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=0)print(x_train.shape, y_train.shape)knn01 = KNN(k=1)knn01.fit(x_train, y_train)print(knn01.score(x_train, y_train))print(knn01.score(x_test, y_test))3.4 调用sklearn
import pandas as pd
import numpy as np
import sys
from sklearn.model_selection import train_test_split # 将数组或矩阵切分为随机训练和测试子集。
from sklearn.neighbors import KNeighborsClassifier# 1. 加载数据(数据一般存在于磁盘或者数据库)
path = '../datas/iris.data'
names = ['A', 'B', 'C', 'D', 'cla']
df = pd.read_csv(path, header=None, names=names, sep=",")# print(df.head())
# print(df.shape)
# print(df["cla"].value_counts())
# sys.exit()# 2. 数据清洗
# NOTE: 不需要做数据处理
def parse_record(row):result = []r = zip(names, row)for name, value in r:if name == 'cla':if value == 'Iris-setosa':result.append(1)elif value == 'Iris-versicolor':result.append(2)elif value == 'Iris-virginica':result.append(3)else:result.append(0)else:result.append(value)return resultdf = df.apply(lambda row: pd.Series(parse_record(row), index=names), axis=1)
df['cla'] = df['cla'].astype(np.int32)
df.info()
# print(df.cla.value_counts())
flag = False
# df = df[df.cla != 3]
# print(df.cla.value_counts())# # 3. 根据需求获取最原始的特征属性矩阵X和目标属性Y
X = df[names[0:-1]]
# print(X.shape)
Y = df[names[-1]]
# print(Y.value_counts())
# sys.exit()# 4. 数据分割
# train_size: 给定划分之后的训练数据的占比是多少,默认0.75
# random_state:给定在数据划分过程中,使用到的随机数种子,默认为None,使用当前的时间戳;给定非None的值,可以保证多次运行的结果是一致的。
x_train, x_test, y_train, y_test = train_test_split(X, Y, train_size=0.6, random_state=28)
print("训练数据X的格式:{}, 以及类型:{}".format(x_train.shape, type(x_train)))
print("测试数据X的格式:{}".format(x_test.shape))
print("训练数据Y的类型:{}".format(type(y_train)))# 5. 特征工程的操作
# NOTE: 不做特征工程# 6. 模型对象的构建
"""
KNN:n_neighbors=5,weights='uniform',algorithm='auto', leaf_size=30,p=2,metric='minkowski', metric_params=None, n_jobs=1
"""
KNN = KNeighborsClassifier(n_neighbors=1, weights='uniform', algorithm='kd_tree')# 7. 模型的训练
KNN.fit(x_train, y_train)# 8. 模型效果评估
train_predict = KNN.predict(x_train)
test_predict = KNN.predict(x_test)
print("KNN算法:测试集上的效果(准确率):{}".format(KNN.score(x_test, y_test)))
print("KNN算法:训练集上的效果(准确率):{}".format(KNN.score(x_train, y_train)))# 模型的保存与加载
import joblibjoblib.dump(KNN, "./knn.m") # 保存模型
# joblib.load() # 加载模型读取训练后的模型
import joblib###1、加载回复模型
knn = joblib.load("./knn.m")###2、对待预测的数据进行预测 (数据处理好后的数据)x = [[5.1, 3.5, 1.4, 0.2]]
y_hat = knn.predict(x)
print(y_hat)
4. 补充
参考《机器学习》-周志华
- KNN学习是
懒惰学习(lazy learning)的著名代表——仅仅是把样本保存起来,训练时间开销为0,待收到测试样本后,再进行处理;而在训练阶段就对样本进行学习处理的方法,称为急切学习(eager learning) - 当k=1时,KNN算法称为
最近邻分类器(1NN)。在处理二分类问题时:给定测试样本x,若其最近邻样本为z,则最近邻分类器出错的概率就是x与z类别标记不同的概率(后续补充)
这篇关于[深度学习]Part2 K临近算法(KNN)Ch02——【DeepBlue学习笔记】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







