[深度学习]Part1 Python学习进阶Ch24图像处理OpenCV（24.14~24.23）——【DeepBlue学习笔记】

本文仅供学习使用

24. 图像处理OpenCV

24.14 轮廓查找与绘制

什么是轮廓： 轮廓可以简单认为成将连续的点（连着边界）连在一起的曲线，具有相同的颜色或者灰度，提取轮廓就是提取
这些具有相同颜色或者灰度的曲线，或者说是连通域，轮廓在形状分析和物体的检测和识别中非常有用。

注意事项:
①为了更加准确，要使用二值化图像。在寻找轮廓之前，要进行阈值化处理或者 Canny 边界检测
②查找轮廓的函数会修改原始图像。如果在找到轮廓之后还想使用原始图像的话，应该将原始图像存储到其他变量中img.copy()
③在OpenCV 中，查找轮廓就像在黑色背景中找白色物体，要找的物体应该是白色而背景应该是黑色。

常用函数:
cv2.findContours()——查找轮廓
cv2.drawContours()——绘制轮廓

24.14.1 查找轮廓——cv2.findContours()

cv2.findContours(image, mode, method[, contours[, hierarchy[,offset]]]) → contours, hierarchy
image: 输入图像, 8位单通道图像(一般为二值图)
contours: 检测到的轮廓, 每个轮廓存储为一个点向量, 即Point类型的vector表示
hierarchy: 可选的输出向量, 包含图像的拓扑信息。其作为轮廓数量的表示, 包含了许多元素, 每个轮廓contours[i]对应4个hierarchy元素hierarchy[i][0]~hierarchy[i][3], 分别表示后一轮廓、前一轮廓、父轮廓、内嵌轮廓的索引编号, 如果没有对应项, 设置为负数
mode: 轮廓检索模式, 取值如下:

cv2.RETR_EXTERNAL=0——表示只检测最外层轮廓
cv2.RETR_LIST=1——提取所有轮廓并放置在list中, 轮廓不建立等级关系
cv2.RETR_CCOMP=2——提取所有轮廓并组织为双层结构
cv2.RETR_TREE =3——提取所有轮廓并重新建立网状轮廓结构

method: 轮廓的近似方法：

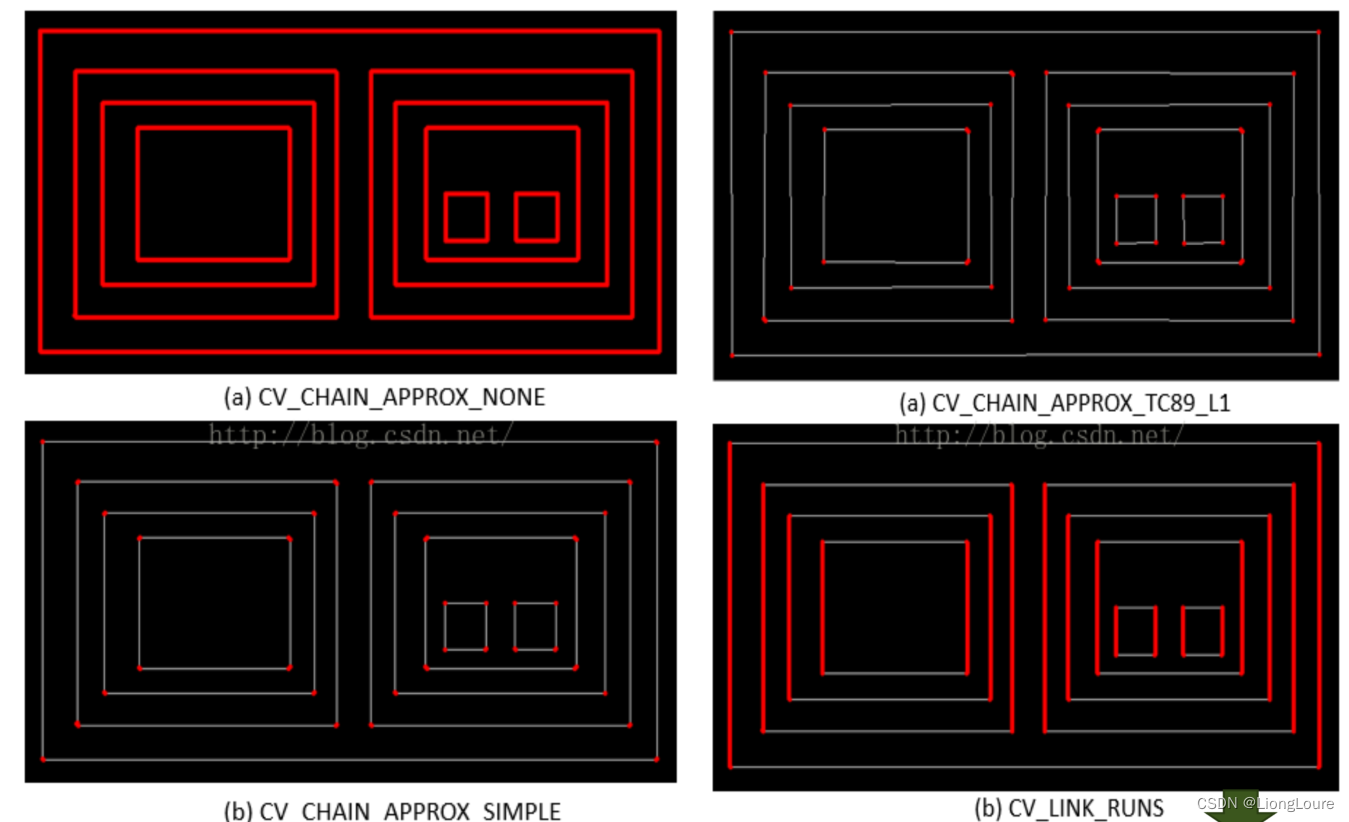
cv2._CHAIN_APPROX_NONE 连续存储所有的轮廓点，任何两个相邻的点都是水平、垂直或者斜相邻的。 max(abs(x1-x2)，abs(y2-y1)=1;
·cv2.CHAIN_APPROX_SIMPLE 压缩存储，对于水平，垂直或者斜向的线段，只会保存端点。比如一个四边形，只会存储四个顶点。
CHAIN_APPROX_TC89_L1 ， CHAIN_QPPROX_TC89_KCOS 使用Teh-Chin链逼近算法中的一个，LINK_RUNS 与上述的算法完全不同，连接所有的水平层次的轮廓。

offset: 每个轮廓的可选偏移量, 默认值Point()

import numpy as np
import cv2image_path = r'D:/datas2/yellowmoon.png'
img = cv2.imread(image_path)
# cv2.imshow('img', img)
# cv2.waitKey(0)img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# cv2.imshow('img_gray', img_gray)
# cv2.waitKey(0)_, thresh = cv2.threshold(img_gray, 0, 255, cv2.THRESH_BINARY+cv2.THRESH_OTSU)
# cv2.imshow('thresh', thresh)
# cv2.waitKey(0)contours,_ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
colors = [[255, 0, 0],[0, 255, 0],[0, 0, 255],[255, 255, 255],[255, 255, 255],[255, 255, 0]]
for idx, cnt in enumerate(contours):cv2.drawContours(img, cnt, -1, colors[idx],thickness=3)
cv2.imshow('draw',img)
cv2.waitKey(0)

24.14.2 绘制轮廓——cv2.drawContours()

cv2.drawContours(image, contours, contourIdx, color, thickness[, linelype[, hierarchyl, maxLevel[,offsetl]]]]) → None
image: 目标图像, Mat类型对象即可
contours: 所有的输入轮廓, 每个轮廓存储为一个点向量
contourIdx: 轮廓绘制指示变量(索引), 若为负值, 则表示绘制所有轮廓
color: 绘制轮廓的颜色
thickness: 轮廓线条的粗细, 默认值1, 如果为负值, 则绘制轮廓内部, 可选宏 CV_FILLED
lineType: 线条类型, 默认值8
hierarcy: 可选的层次结构信息, 默认值noArray()
maxLevel: 表示用于绘制轮廓的最大等级, 默认值INT_MAX
offset: 可选的轮廓偏移参数, 默认值Point()

24.14.3 访问轮廓

1. 访问每一个轮廓：

import numpy as np
import cv2image_path = r'D:/datas2/yellowmoon.png'
img = cv2.imread(image_path)
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
_, thresh = cv2.threshold(img_gray, 0, 255, cv2.THRESH_BINARY+cv2.THRESH_OTSU)contours,_ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)# 1
for i in range(0,len (contours)):#cv2.drawContours(img,contours[i],-1,(0,255,0),5)cv2.drawContours(img,contours,i,(0,255,0),5)cv2.imshow('draw',img)cv2.waitKey(0)# 2
for cnt in contours:cv2.drawContours(img,cnt,-1,(0,255,0),5) cv2.imshow('draw',img)cv2.waitKey(0)

2. 访问每一个轮廓的所有点

import numpy as np
import cv2image_path = r'D:/datas2/yellowmoon.png'
img = cv2.imread(image_path)
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
_, thresh = cv2.threshold(img_gray, 0, 255, cv2.THRESH_BINARY+cv2.THRESH_OTSU)contours,_ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
# 访问每个轮廓的每个点# 1
for i in range(0,len (contours)):for j in range(0,len (contours[i])):cv2.drawContours(img,contours[i],j,(0,255,0),3)cv2.imshow('draw',img)cv2.waitKey(0)
cv2.imshow('draw',img)
cv2.waitKey(0)# 2
for cnt in contours:for j in range(0,len (cnt)):cv2.drawContours(img,cnt,j,(0,255,0),3)cv2.imshow('draw',img)cv2.waitKey(0)

len(contours)——所有轮廓的个数
len(contours[i])——第i个轮廓所有点的个数

24.15 轮廓特征属性及应用

24.15.1 凸包

（待补充）

24.15.2 使用特定形状的轮廓包围

在实际应用中, 经常会有将检测到的轮廓用多边形表示出来的需求, 提取包围轮廓的多边形也方便我们做进一步分析, 轮廓包围主要有一下几种:
◼ 轮廓外接矩形
◼ 轮廓最小外接矩形(旋转)
◼ 轮廓最小包围圆形
◼ 轮廓拟合椭圆
◼ 轮廓逼近多边形曲线

轮廓外接矩形——cv2.boundingRect()

cv2.boundingRect(points) → retval
points: 输入的二维点集
返回值: Rect类矩形对象(x,y,w,h)

import numpy as np
import cv2image_path = r'D:/datas2/yellowmoon.png'
img = cv2.imread(image_path)
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
_, thresh = cv2.threshold(img_gray, 0, 255, cv2.THRESH_BINARY+cv2.THRESH_OTSU)contours,_ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
colors = [[255, 0, 0],[0, 255, 0],[0, 0, 255],[255, 255, 255],[255, 255, 255],[255, 255, 0]]
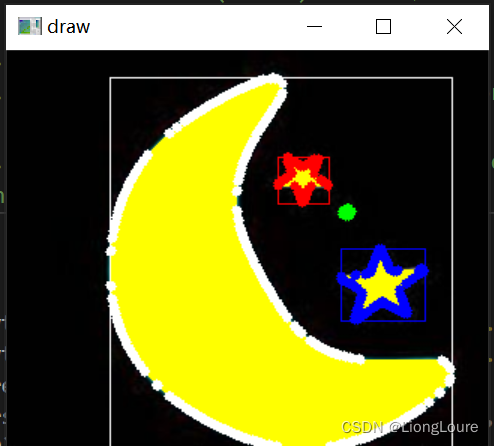
for idx, cnt in enumerate(contours):cv2.drawContours(img, cnt, -1, colors[idx], thickness=5)# 获取外接矩形x, y, w, h = cv2.boundingRect(cnt)cv2.rectangle(img, (x, y), (x+w, y+h), colors[idx])cv2.imshow('draw',img)cv2.waitKey(0)

轮廓最小外接矩形-——cv2.minAreaRect()

cv2.minAreaRect(points) → retval
points: 输入的二维点集
返回值: RotatedRect类矩形对象, 外接旋转矩形主要成员有center、size、 angle
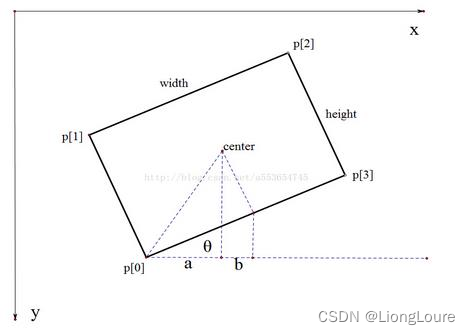
在opencv中，坐标的原点在左上角，与x轴平行的方向为角度为0，逆时针旋转角度为负，顺时针旋转角度为正。而RotatedRect类是以矩形的哪一条边与x轴的夹角作为角度的呢？angle 是水平轴（x轴）逆时针旋转，与碰到的第一个边的夹角，而opencv默认把这个边的边长作为width，angle的取值范围必然是负的

reval = cv2.minAreaRect(cnt) # 中心点坐标，(w,h)，angle
box = cv2.boxPoints(reval) # 矩形4个点的坐标集合，分别是左上角，右上角，左下角，右下角

import numpy as np
import cv2image_path = r'D:/datas2/yellowmoon.png'
img = cv2.imread(image_path)
img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
_, thresh = cv2.threshold(img_gray, 0, 255, cv2.THRESH_BINARY+cv2.THRESH_OTSU)contours,_ = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
colors = [[255, 0, 0],[0, 255, 0],[0, 0, 255],[255, 255, 255],[255, 255, 255],[255, 255, 0]]
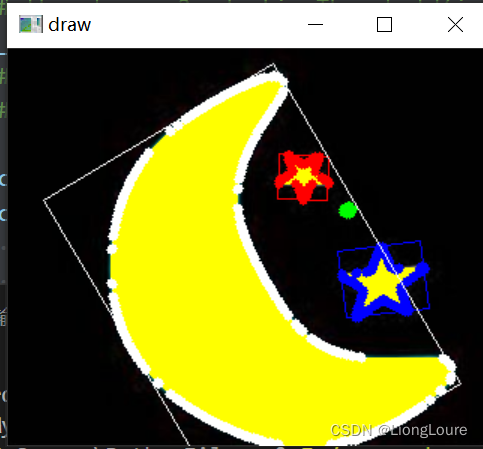
for idx, cnt in enumerate(contours):cv2.drawContours(img, cnt, -1, colors[idx], thickness=5)# 最小外接矩形reval = cv2.minAreaRect(cnt)# 中心点坐标，(w,h)，anglebox = cv2.boxPoints(reval)# 矩形4个点的坐标集合，分别是左上角，右上角，左下角，右下角box = np.int0(box)cv2.drawContours(img, [box], -1, colors[idx])# cv2.rectangle(img, box[0], box[2], colors[idx])cv2.imshow('draw',img)
cv2.waitKey(0)

轮廓最小外接圆——cv2.minEnclosingCircle()

cv2.minEnclosingCircle(points) → center,radius
points: 输入的二维点集
center: Point2f&类型的center, 圆的输出圆心
radius: float&类型, 表示圆的输出半径

轮廓椭圆拟合——cv2.fitEllipse()

cv2.fitEllipse(points) → retval
points: 输入的二维点集, 可以填Mat类型或std::vector
返回值: RotatedRect类旋转矩形对象

逼近多边形曲线——cv2.approxPolyDP()

cv2.approxPolyDP(curve,epsilon,closed[,approxCurve]) → retval
curve: 输入的二维点集或轮廓
approxCurve: 多边形逼近的结果, 其类型和输入二维点集类型一致
epsilon: 逼近的精度, 为原始曲线和近似曲线间的最大值
closed: 如果其为真, 则近似的曲线为封闭曲线, 否则近似的曲线不封闭

计算轮廓面积——cv2.contourArea()

cv2.contourArea(contour[,oriented]) → retval
contour: 输入的二维点集或轮廓
oriented: 默认值false, 表示返回面积为绝对值, 否则带符号
返回值: double类型返回轮廓面积

计算轮廓长度(周长或者曲线长度)——cv2.arcLength()

cv2.arcLength(curve,closed) → retval
curve: 输入的二维点集或轮廓
colsed: 用于指示曲线是否封闭的标识符, 默认值true, 表示曲线封闭
返回值: double类型返回轮廓长度

注:cv2.contourArea()&& cv2.arcLength()可用于轮廓删选

24.15.3 点与轮廓的距离及位置关系

计算点与轮廓的距离及位置关系——cv2.pointPolygonTest()

cv2.pointPolygonTest(contour,pt,measureDist) → retval
contour: 所需检测的轮廓对象
pt: Point2f 类型的pt, 待判定位置的点
measureDist: 是否计算距离的标志, 当其为true时, 计算点到轮廓的最短距离, 当其为false时, 只判定轮廓与点的位置关系, 具体关系如下:
①返回值为-1, 表示点在轮廓外部
②返回值为0, 表示点在轮廓上
③返回值为1, 表示点在轮廓内部

注意∶如果你不需要知道具体距离，建议你将第三个参数设为 False，这样速度会提高2到3倍。

24.15.4 轮廓的矩

1. 零阶矩
   根据矩的定义，二维图像的灰度用 $f(x,y)$ 表示，零阶矩 $m_{00}$ ，表示的是图像灰度的总和:
   $m_{00}=\iint f(x,y)dxdy$
2. 一阶矩
   图像的一阶矩 $m_{10}$ 和 $m_{01}$ 表示用来确定图像的灰度中心，根据中心矩的定义很容易计算出，${\mu }_{10}=0,{\mu }_{01}=0$
   $\bar{x}=\frac{m_{10}}{m_{00}},\bar{y}=\frac{m_{01}}{m_{00}}$，其中$m_{10}=\sum _x\sum _{y}xf(x,y)$，$m_{01}=\sum _x\sum _{y}yf(x,y)$
3. 二阶矩
   二阶矩有三个，$m_{11},m_{02},m_{20}$，也成为惯性矩。它们可以确定物体的几个特性：
   ① 二阶中心矩用来确定目标物体的主轴，长轴和短轴分别对应最大和最小的二阶中心矩。可以计算主轴方向角。
   ② 图像椭圆： 由一阶、二阶矩可以确定一个与原图像惯性等价的图像椭圆。所谓图像椭圆是一个与原图像的二阶矩及原图像的灰度总和均相等的均匀椭圆。使得主轴与图像的主轴方向重合，一边分析图像性质。
   $m_{11}=\sum _x\sum _{y}xyf(x,y)$
   $m_{02}=\sum _x\sum _y{y}^{2}f(x,y)$
   $m_{20}=\sum _x\sum _y{x}^{2}f(x,y)$
4. 三阶矩及以上
   对于三阶或三阶以上矩,使用图像在轴或轴上的投影比使用图像本身的描述更方便。
   三阶矩：投影扭曲，描述了图像投影的扭曲程度。扭曲是一个经典统计量,用来衡量关于均值对称分布的偏差程度。
   四阶矩：投影峰度，峰度是一个用来测量分布峰度的经典统计量。可以计算峰度系数。当峰度系数为0时,表示高斯分布；当峰度系数小于0时,表示平坦的少峰分布；当峰度系数大于0时,表示狭窄的多峰分布。
5. Hu矩
   直接用原点矩或中心矩作为图像的特征,不能保证特征同时具有平移、旋转和比例不变性。事实上,如果仅用中心矩表示图像的特征,则特征仅具有平移不变性如果利用归一化中心矩,则特征不仅具有平移不变性,而且还具有比例不变性,但具有旋转不变性。要同时具有平移、旋转和比例变换不变性,直接使用原点矩或中心矩是不行的。为此提出了不变矩,他给出了连续函数矩的定义和关于矩的基本性质,证明了有关矩的平移不变性、旋转不变性以及比例不变性等性质,具体给出了具有平移不变性、旋转不变性和比例不变性的七个不变矩的表达式。
   不变矩(Invariant Moments)是一处高度浓缩的图像特征，具有平移、灰度、尺度、旋转不变性。M.K.Hu在1961年首先提出了不变矩的概念。下面是几个图像的不变矩：
   一幅 $M\times N$ 的数字图像 $f(i,j)$ ，其中 $p+q$ 阶几何矩 $m_{pq}$ 和中心距 ${\mu }_{pq}$ 为：
   $m_{pq}=\sum _{i=1}^M\sum _{j=1}^N{x}^p{y}^{q}f(i,j)$
   ${\mu }_{pq}=\sum _{x=1}^M\sum _{y=1}^N{(i-\bar{i})}^p{(j-\bar{j})}^{q}f(i,j)$
   其中 $f(i,j)$ 为图像在坐标点 $(i,j)$ 处的灰度值。$\bar{i}=\frac{m_{10}}{m_{00}},\bar{j}=\frac{m_{01}}{m_{00}}$
   若将$m_{00}$ 看做是图像的 灰度质量，则 $(\bar{i},\bar{j})$ 为图像的质心坐标，那么中心距 ${\mu }_{pq}$ 反映的是图像灰度相对于其灰度质心的分布情况。可以用几何矩来表示中心距，0~3阶中心距与几何矩的关系如下：
   $\{\begin{array}{c}{\mu }_{00}=\sum _{i=1}^M\sum _{j=1}^N{(i-\bar{i})}^0{(j-\bar{j})}^{0}f(i,j)=m_{00}\\ {\mu }_{10}=\sum _{i=1}^M\sum _{j=1}^N{(i-\bar{i})}^1{(j-\bar{j})}^{0}f(i,j)=0\\ {\mu }_{01}=\sum _{i=1}^M\sum _{j=1}^N{(i-\bar{i})}^0{(j-\bar{j})}^{1}f(i,j)=0\\ {\mu }_{11}=\sum _{i=1}^M\sum _{j=1}^N{(i-\bar{i})}^1{(j-\bar{j})}^{1}f(i,j)=m_{11}-\bar{y}{m}_{10}\\ {\mu }_{20}=\sum _{i=1}^M\sum _{j=1}^N{(i-\bar{i})}^2{(j-\bar{j})}^{0}f(i,j)=m_{20}-\bar{y}{m}_{01}\\ {\mu }_{02}=\sum _{i=1}^M\sum _{j=1}^N{(i-\bar{i})}^0{(j-\bar{j})}^{2}f(i,j)=m_{02}-\bar{y}{m}_{01}\\ {\mu }_{30}=\sum _{i=1}^M\sum _{j=1}^N{(i-\bar{i})}^3{(j-\bar{j})}^{0}f(i,j)=m_{30}-\bar{x}{m}_{02}+2{\bar{x}}^2{m}_{10}\\ {\mu }_{12}=\sum _{i=1}^M\sum _{j=1}^N{(i-\bar{i})}^1{(j-\bar{j})}^{2}f(i,j)=m_{12}-2\bar{y}{m}_{11}-\bar{x}{m}_{02}+2{\bar{y}}^2{m}_{10}\\ {\mu }_{21}=\sum _{i=1}^M\sum _{j=1}^N{(i-\bar{i})}^2{(j-\bar{j})}^{1}f(i,j)=m_{21}-2\bar{x}{m}_{11}-\bar{y}{m}_{02}+2{\bar{x}}^2{m}_{01}\end{array}$
   而数字图像是一个二维的离散信号，对上述公式进行离散化之后，其中C与R分别表示图像的列与行。
   $m_{pq}=\sum _{i=1}^C\sum _{j=1}^R{x}^p{y}^{q}f(x,y)p,q=0,1,2,...$
   0阶矩（$m_{00}$）:目标区域的质量
   1阶矩（$m_{10},m_{01}$）：目标区域的质心
   2阶矩（$m_{11},m_{02},m_{20}$）：目标区域的旋转半径
   3阶矩（$m_{03},m_{12},m_{21},m_{30}$）：目标区域的方位和斜度，反应目标的扭曲但是目标区域往往伴
   随着空间变换（平移，尺度，旋转），所以需要在普通矩的基础上构造出具备不变性的矩组——hu矩。
   中心矩：构造平移不变性——由零阶原点矩和一阶原点矩，我们可以求得目标区域的质心坐标：$\bar{x}=\frac{m_{10}}{m_{00}},\bar{y}=\frac{m_{01}}{m_{00}}$
   由求得的质心坐标，我们可以构造出中心矩，质心为中心构建中心矩，矩的计算是目标区域中的点相对于目标区域的质心，而与目标区域的位置无关，及具备了平移不变性。
   ${\mu }_{pq}=\sum _{x=1}^C\sum _{y=1}^R{(x-\bar{x})}^p{(y-\bar{y})}^{q}f(x,y)p,q=0,1,2,...$
   归一化中心矩：构造尺度不变性——为抵消尺度变化对中心矩的影响，利用零阶中心矩u00对各阶中心距进行归一化处理，得到归一
   化中心矩，其中：$r=\frac{p+q+2}{2},p+q=2,3,...$
   ${\eta }_{pq}=\frac{{\mu }_{pq}}{{{\mu }_{00}}^r}$
   利用二阶和三阶规格中心矩可以导出下面7个不变矩组(${\Phi }_1\sim {\Phi }_7$)，它们在图像平移、旋转和比例变化时保持不变。
   $\{\begin{array}{c}{\Phi }_1={\eta }_{20}+{\eta }_{02}\\ {\Phi }_2={({\eta }_{20}-{\eta }_{02})}^2+4{{\eta }_{11}}^2\\ {\Phi }_3={({\eta }_{20}-3{\eta }_{12})}^2+3{({\eta }_{21}-{\eta }_{03})}^2\\ {\Phi }_4={({\eta }_{30}+{\eta }_{12})}^2+{({\eta }_{21}+{\eta }_{03})}^2\\ {\Phi }_5=({\eta }_{30}+3{\eta }_{12})({\eta }_{30}+{\eta }_{12})[{({\eta }_{30}+{\eta }_{12})}^2-3{({\eta }_{21}+{\eta }_{03})}^2]+(3{\eta }_{21}-{\eta }_{03})({\eta }_{21}+{\eta }_{03})[3{({\eta }_{30}+{\eta }_{12})}^2-{({\eta }_{21}+{\eta }_{03})}^2]\\ {\Phi }_6=({\eta }_{20}-{\eta }_{02})[{({\eta }_{30}+{\eta }_{12})}^2-{({\eta }_{21}+{\eta }_{03})}^2]+4{\eta }_{11}({\eta }_{30}+{\eta }_{12})({\eta }_{21}+{\eta }_{03})\\ {\Phi }_7=(3{\eta }_{21}-{\eta }_{03})({\eta }_{30}+{\eta }_{12})[{({\eta }_{30}+{\eta }_{12})}^2-3{({\eta }_{21}+{\eta }_{03})}^2]+(3{\eta }_{21}-{\eta }_{03})({\eta }_{21}+{\eta }_{03})[3{({\eta }_{30}+{\eta }_{12})}^2-{({\eta }_{21}+{\eta }_{03})}^2]\end{array}$

矩的计算——cv2.moments()

cv2.moments(arrayl,binaryImage])) → retval
array: 输入参数, 可以是光栅图像或二维数组
binaryImage: 默认值false, 非零像素取其本身值, 若为true, 则非零像素取1
返回值: Moments类的对象, 返回对应的轮廓的空间矩/中心矩和归一化中心矩(最高3阶)

24.15.5 形状匹配—比较两个形状或轮廓间的相似度cv2.matchShapes()

cv2.matchShapes(contour1,contour2,method,parameter) → retval
contour1: 所需比较的轮廓1
contour2: 所需比较的轮廓2
method: 轮廓比较的方法

method = CV_CONTOURS_MATCH_I1 $I_1(A,B)=\sum _{i=1,...,7}\left|\frac{1}{m_i^A}-\frac{1}{m_i^B}\right|$
method = CV_CONTOURS_MATCH_I2 $I_2(A,B)=\sum _{i=1,...,7}\left|m_i^A-m_i^B\right|$
method = CV_CONTOURS_MATCH_I3 $I_3(A,B)=\underset{i=1,...,7}{\max }\frac{|m_i^A-m_i^B|}{|m_i^A|}$
其中：$m_i^A=sign(h_i^A)\cdot \log h_i^A,m_i^B=sign(h_i^B)\cdot \log h_i^B$，$h_i^A,h_i^B$为矩阵A、B的Hu矩

parameter: 比较方法的特殊参数(目前不支持)

注意: cv2.matchShapes()函数比较轮廓相似度是基于Hu矩来计算的, 结果越小相似度越高。Hu矩是归一化中心矩的线性组合, 是为了获取图像某个特征的矩函数(对应变化如平移、缩放、旋转、镜像)

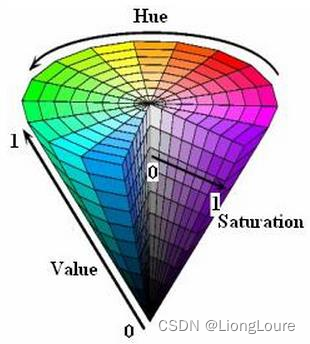
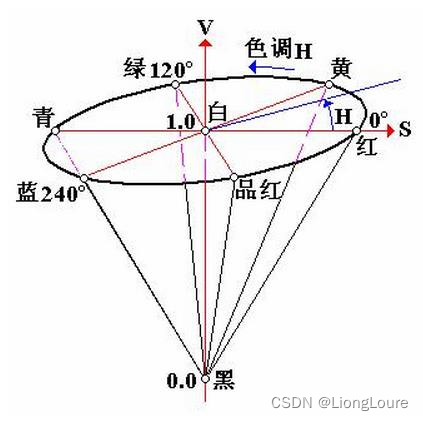
24.15.6 HSV颜色空间

HSV颜色空间与人眼所看色彩较接近, 故常用于颜色检测与识别。其中H(色调)、S(饱和度)、V(亮度)

H—不同的颜色(红色/绿色/蓝色)—范围: 0~360
S—颜色深浅(浅红/深红)—范围: 0.0~1.0
V—颜色亮暗(暗红/亮红)—范围: 0.0~1.0

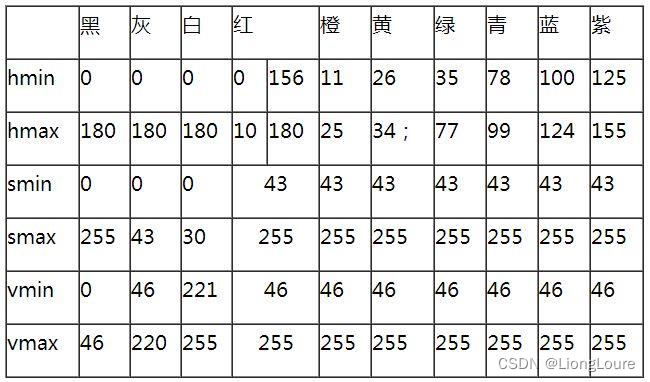
OpenCV默认的HSV范围分别是: H: 0~180, S: 0~255, V: 0~255

1. 颜色空间转换——cv2.cvtColor()
   
   

import cv2
import numpy as npimg = cv2.imread('D:/datas2/logo.png')
img_hsv = cv2.cvtColor(img, cv2.COLOR_BGR2HSV)
lower = np.array([100,43,46],dtype='uint8')
high =  np.array([124,255,255],dtype='uint8')
mask = cv2.inRange(img_hsv,lower,high)
cv2.imshow('mask',mask)
cv2.waitKey(0)

2. 颜色区间范围删选——cv2.inRange()

cv2.inRange(src,lowerb,upperb[,dst]) → dst
src: 输入原图或数组
lowerb: 低边界或者颜色阈值
upperb: 高边界或者颜色阈值
dst: 输出目标图像, 需要和原图一样的size并且类型需为CV_8U

3. 滑动条HSV参数debug工具
   (待补充)

24.16 分水岭算法及图像修补

(待补充)

24.17 GrabCut & FloodFill图像分割

(待补充)

24.18 角点检测简介

(待补充)

24.19 特征检测与匹配

(待补充)

24.20 运动物体检测

(待补充)

24.21 运动物体跟踪(meanShift & CamShift)

(待补充)

24.22 简单人脸检测实例

(待补充)

24.23 简单人脸识别实例

(待补充)