本文主要是介绍131.乐理基础-快速识别音程(一),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
上一个内容:130.乐理基础-倍增音程、倍减音程-CSDN博客
上一个内容里练习的答案:

开始不用数音数就可以辨别音程的方法,首先是不含升降号记号的两个音(两个白键)该怎样判断
方法的核心,就是音名中e-f和b-c这两对是紧紧挨在一起的
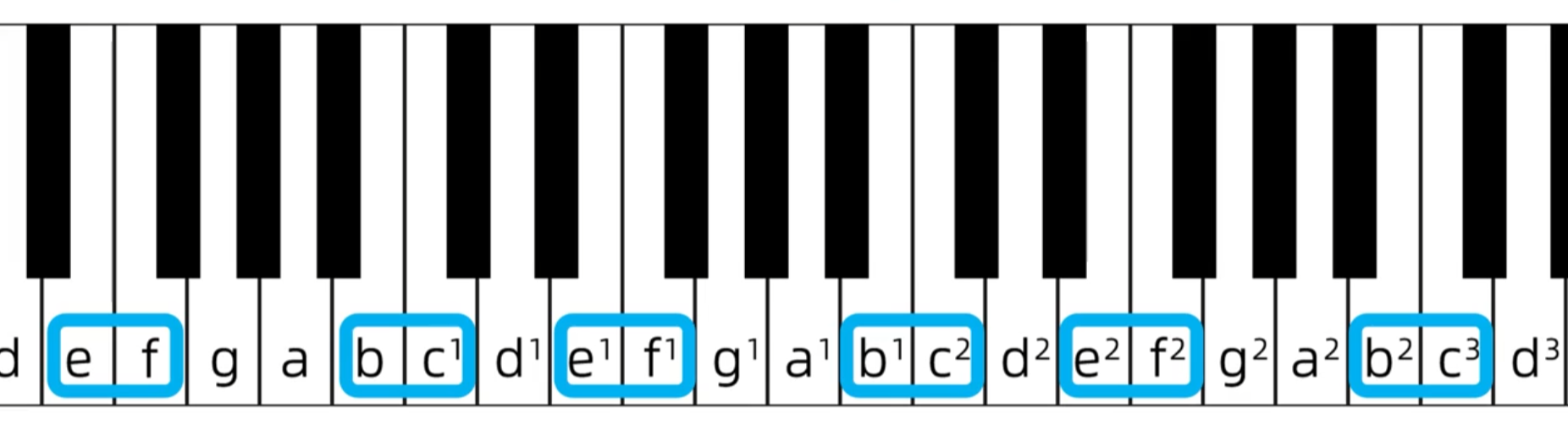
要一眼识别某个音程到底是大是小还是纯,就是通过看看这个音程有没有包含e-f或b-c,首先是一度,一度是c-c、a-a、b-b等这个没必要写,所以直接看二度,二度只有e-f和b-c这两对是紧紧相邻的
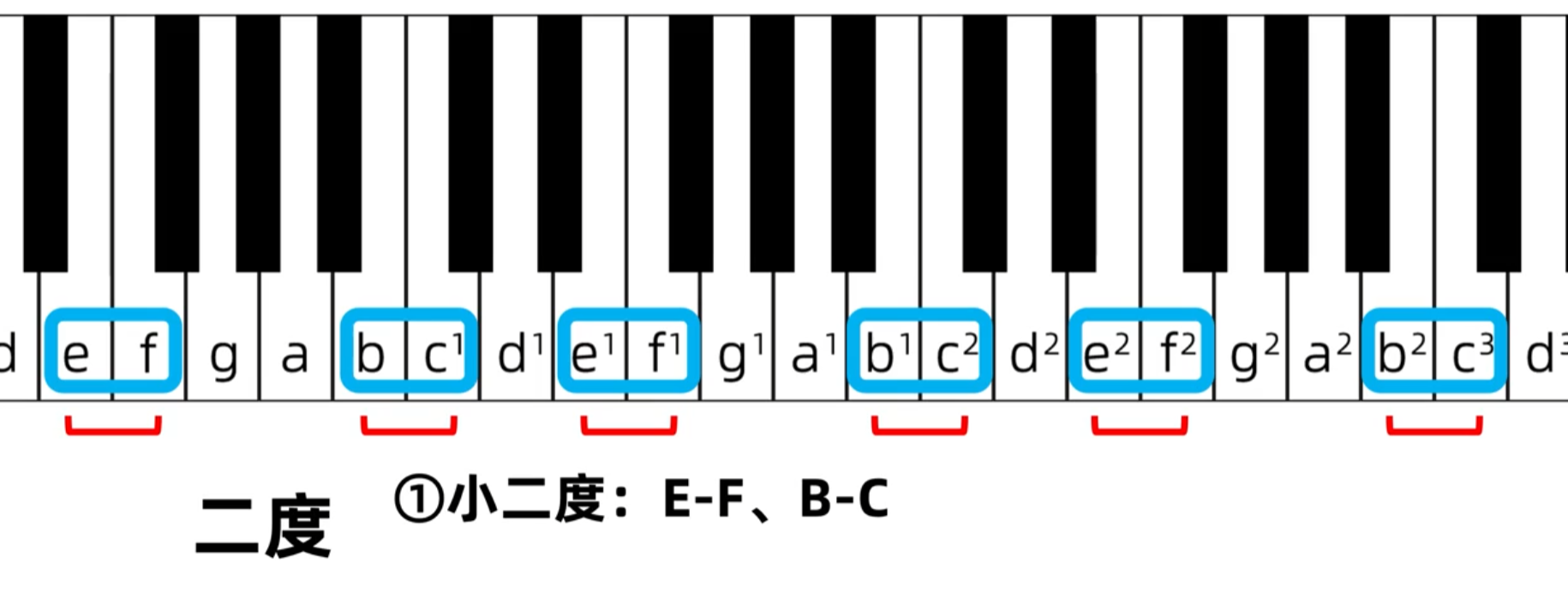
其它不涉及升降号的二度,也就是c-d、d-e、f-g、g-a、a-b这五个,然后这五个距离肯定就要远一点,因为它们之间都夹杂这黑键,如下图a-b的例子
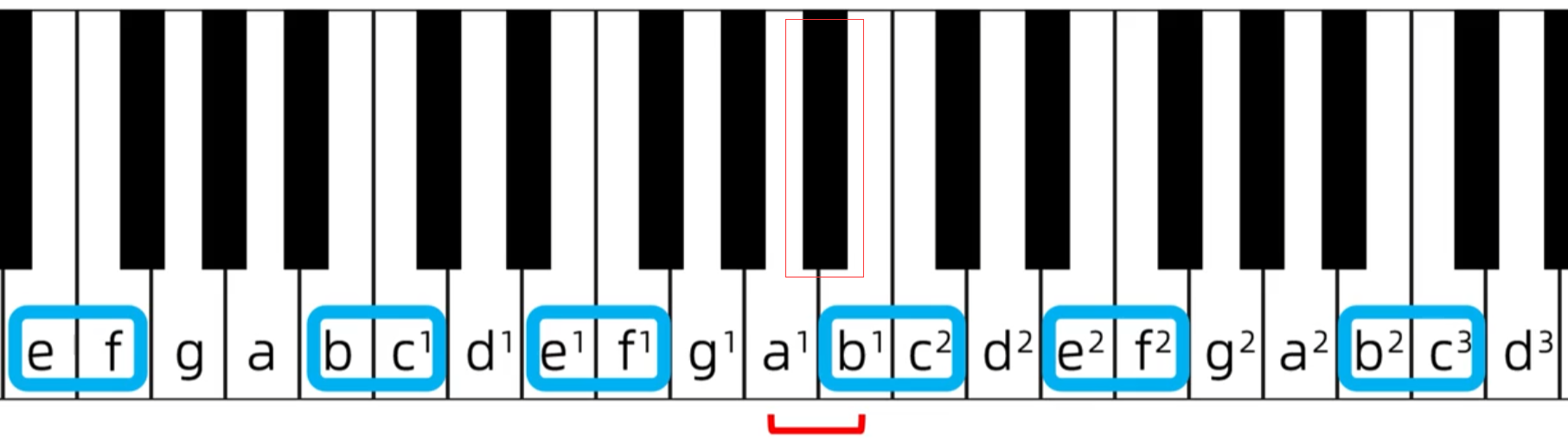
所以这五个一定是大二度
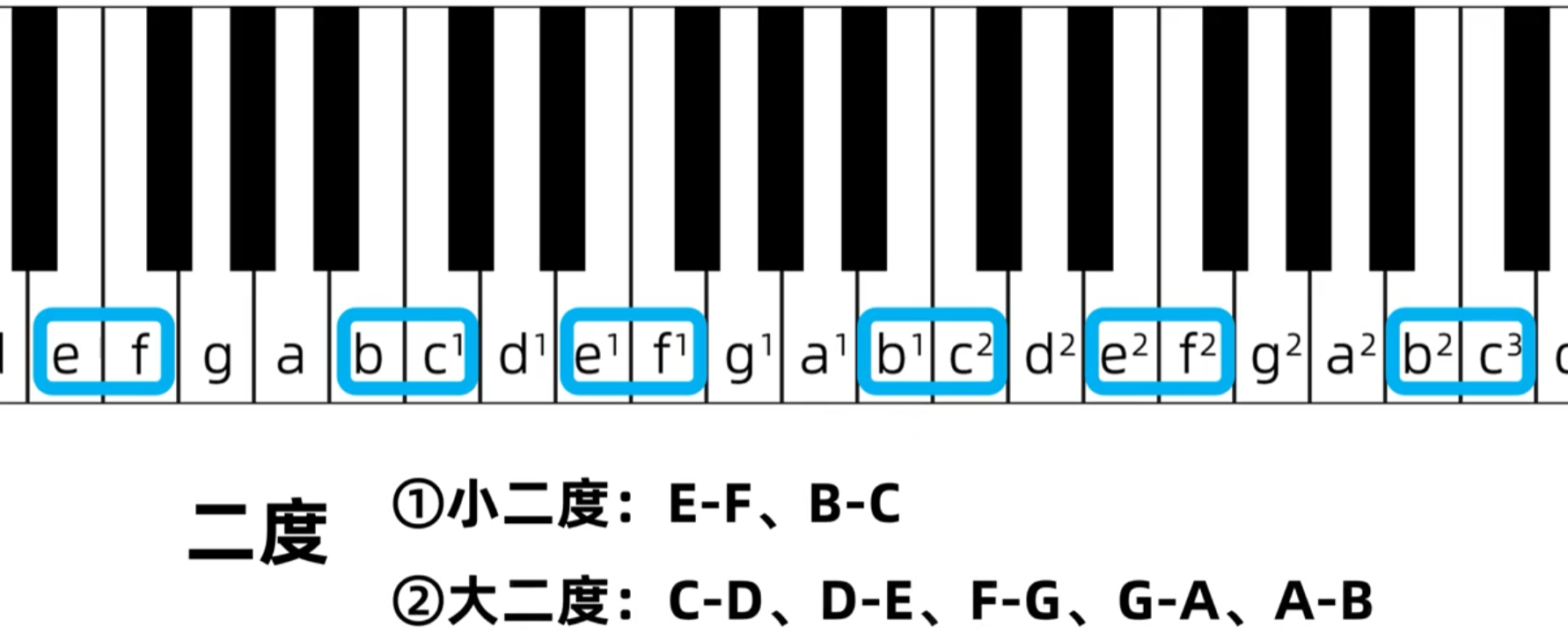
然后三度,首先如果某个三度包含了e-f或者b-c,则距离小一点,如果某个三度不包含e-f或b-c,则距离大一点

比如c-e,它就不包含e-f或b-c所以它的距离就大一点,所以c-e它就是大三度,这就没有再去数什么音数了,直接就去思考有没有包含e-f或b-c
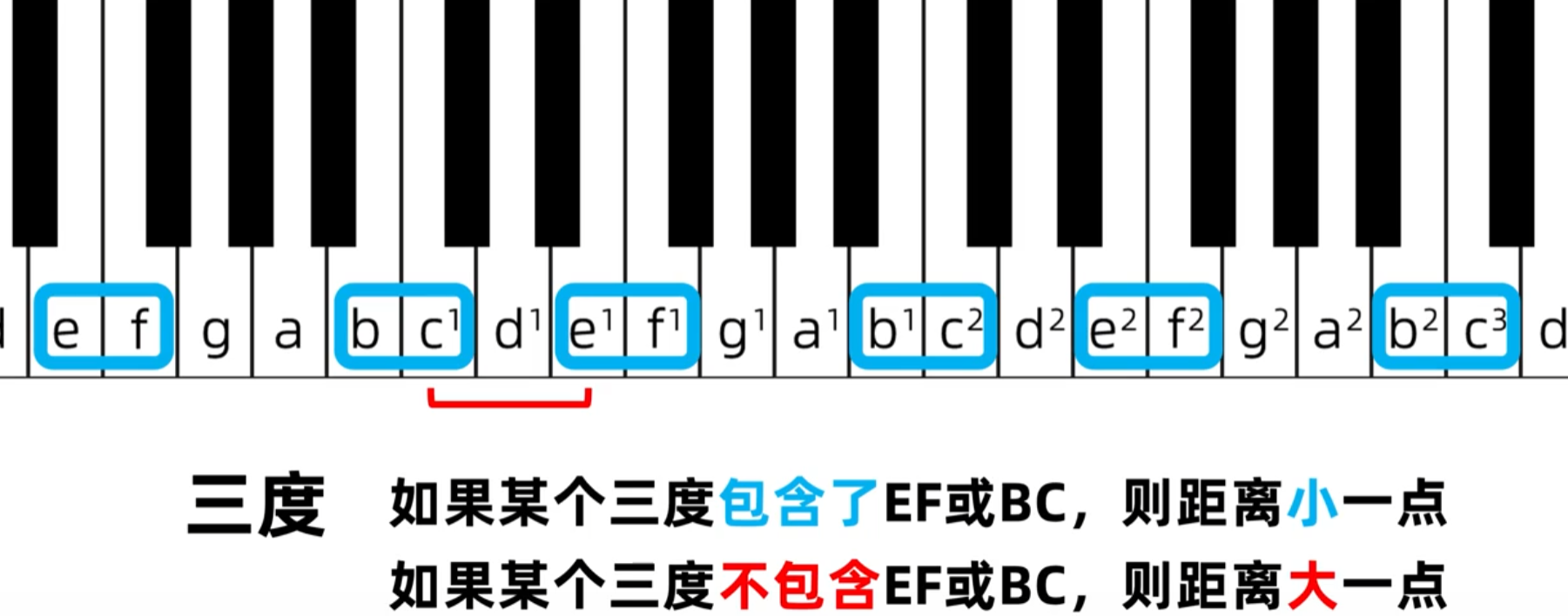
然后d-f,e-f之间没有黑键所以它距离必定会短
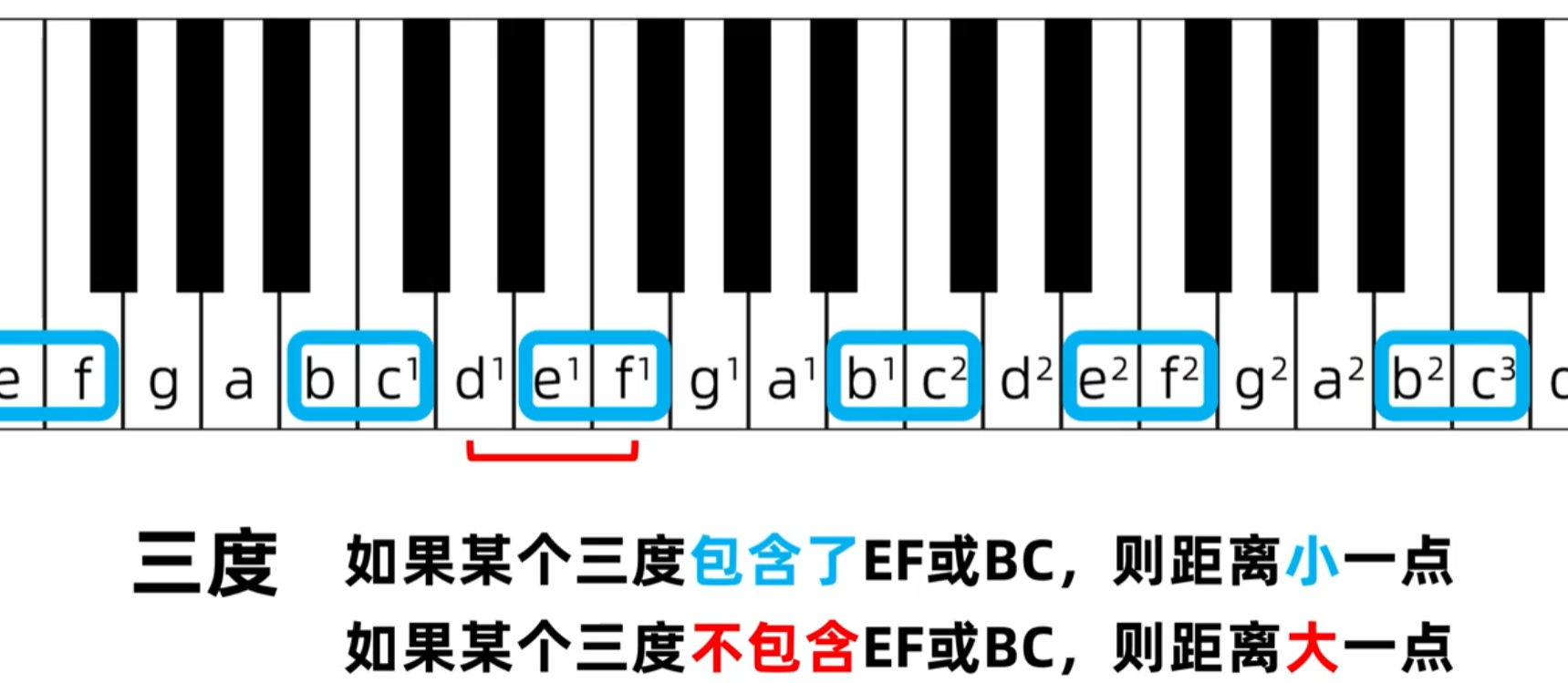
e-g距离短
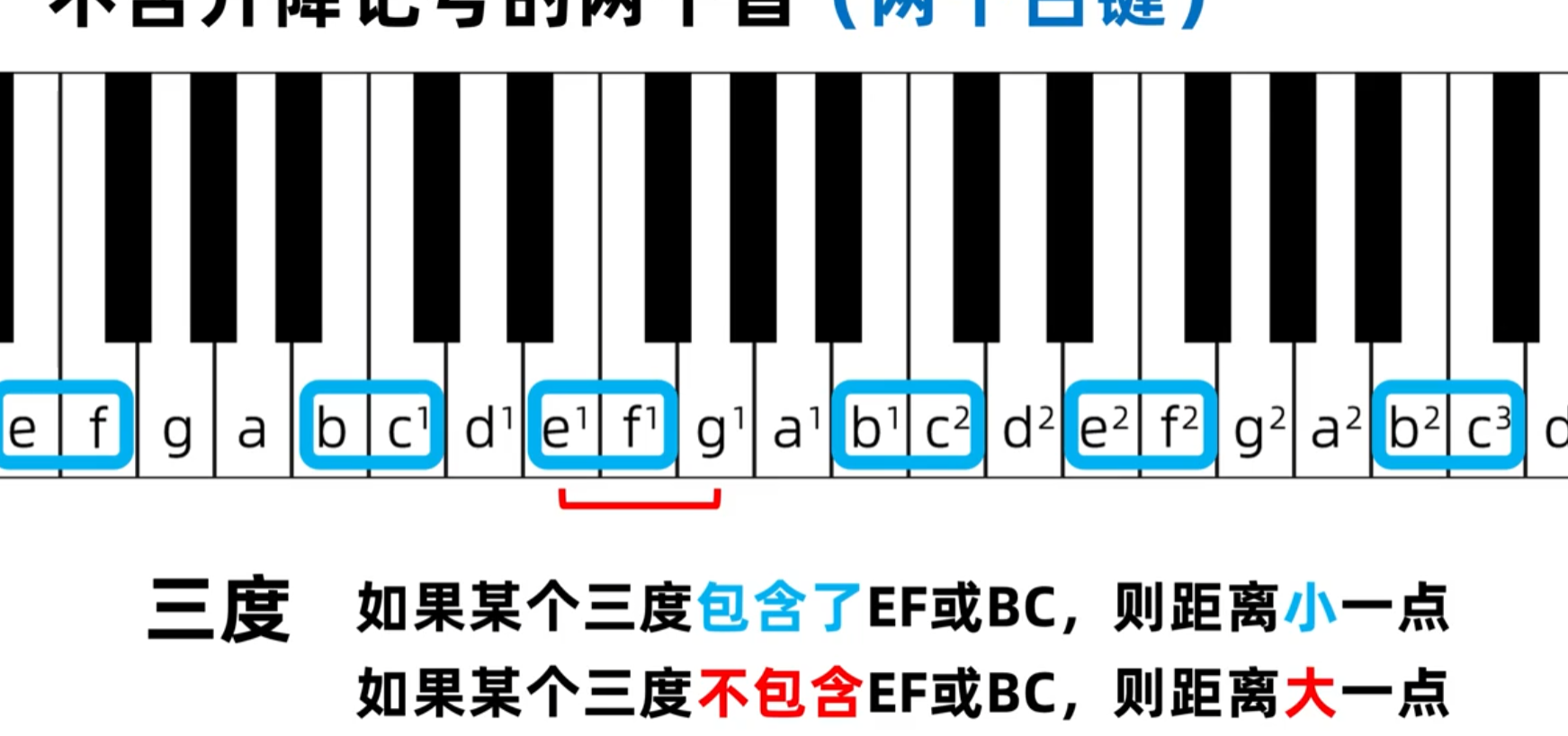
f-a距离长
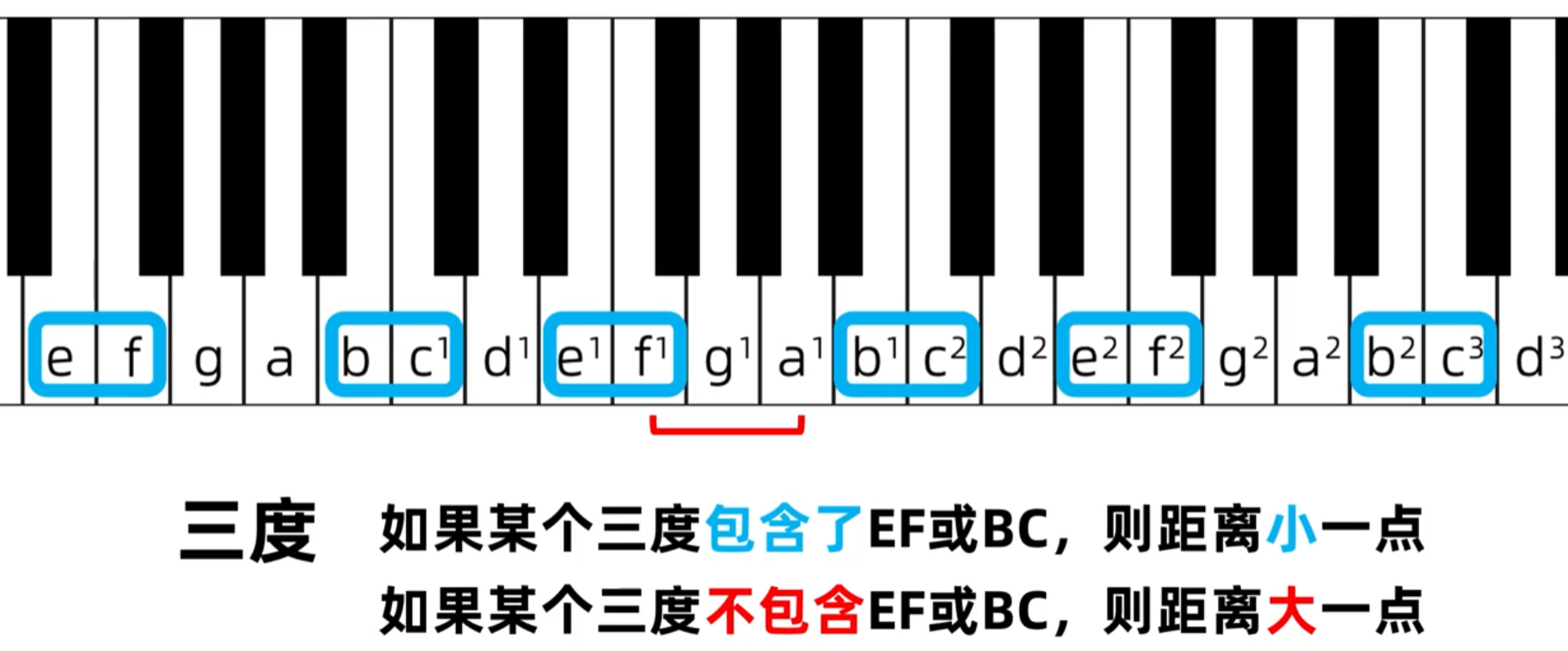
g-b距离长
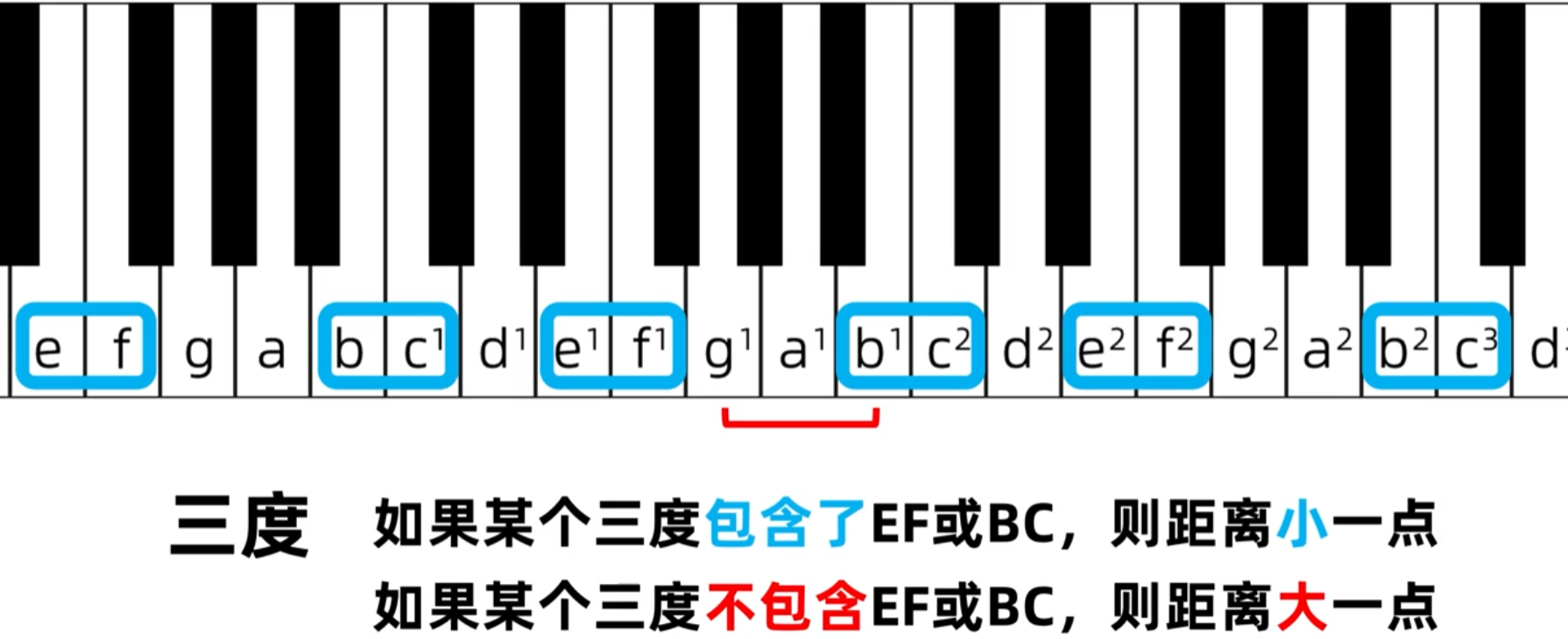
a-c距离短,所以它也是小三度
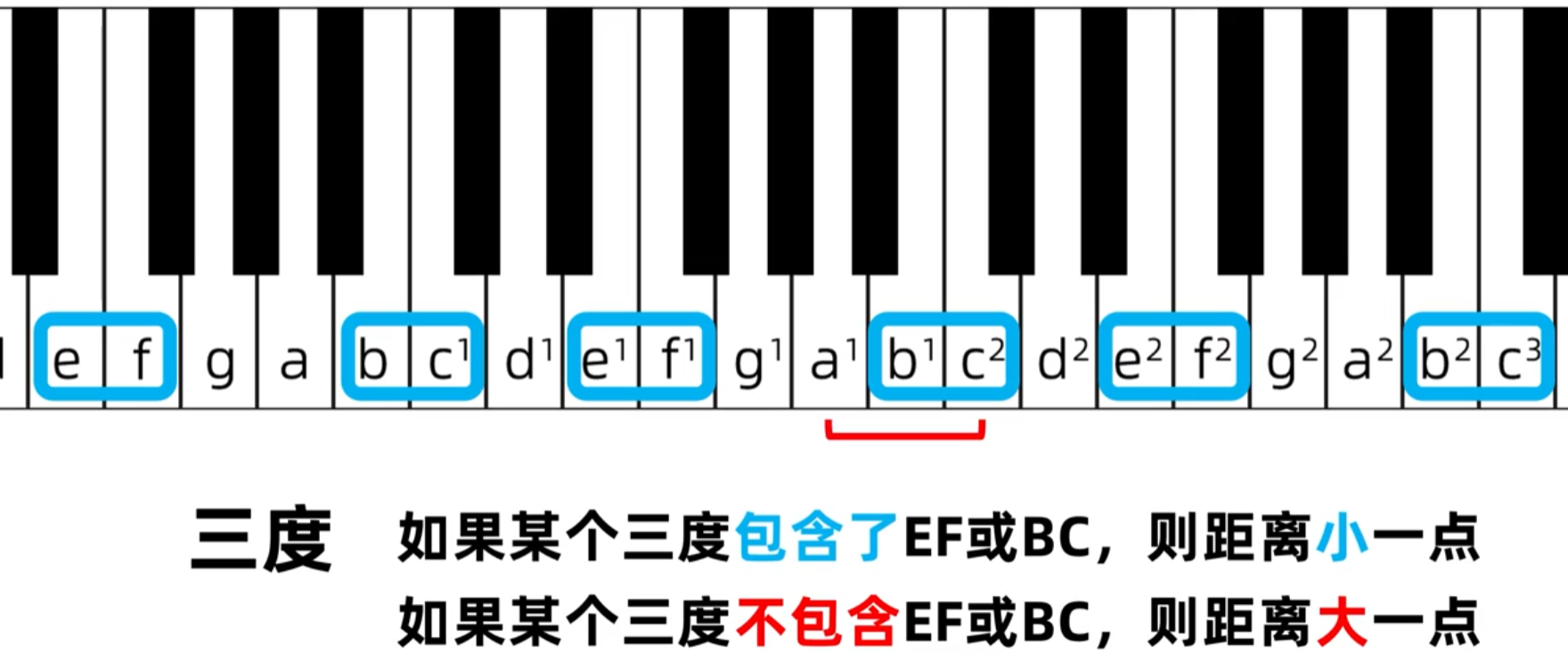
b-d包含了b-c距离短,是小三度,再继续就是下一个组的c-e
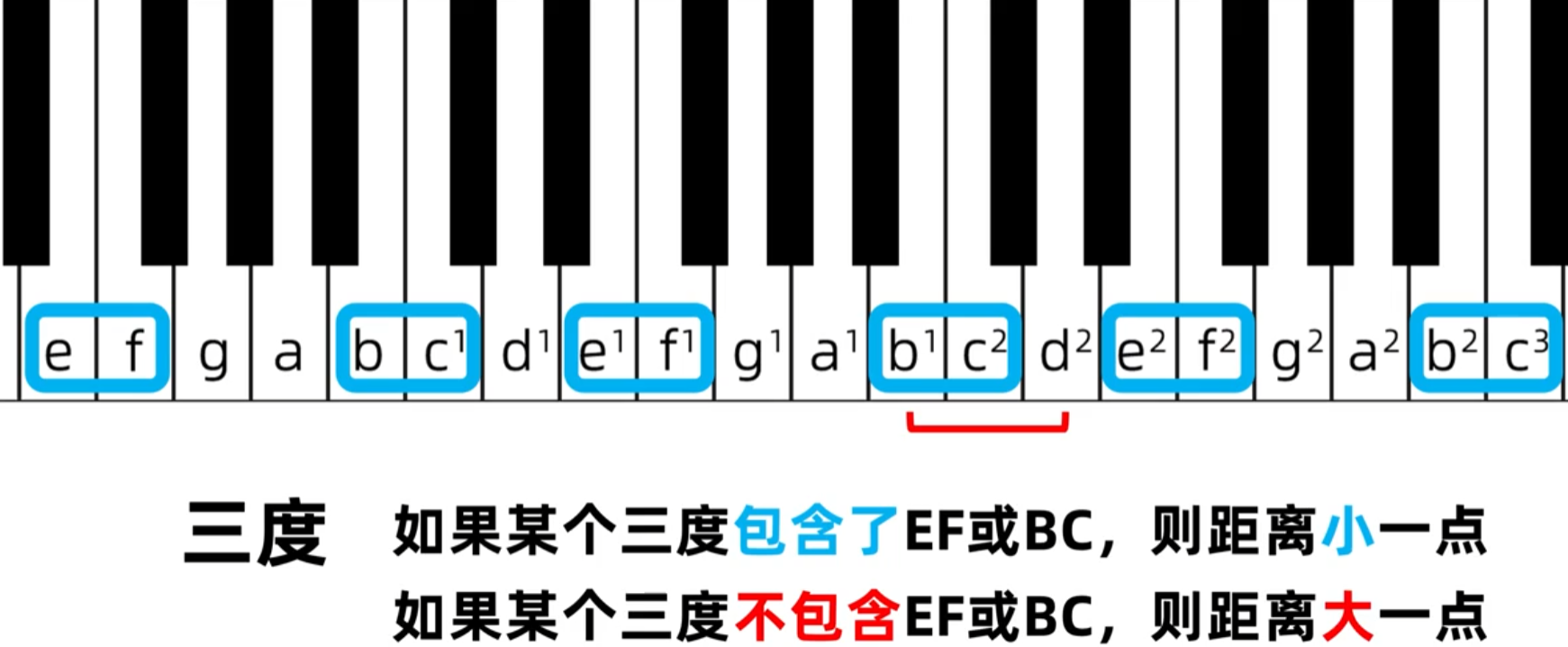
循环都是一样的道理
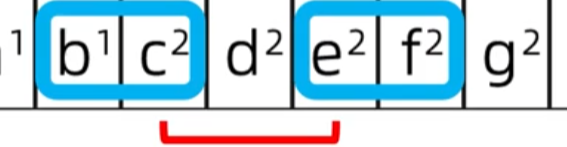
什么音到什么音只要没有特殊标记,左边的音一定比右边的音低的,如下图红框里的a-c这个a一定比c低,它们不一定是一个组的

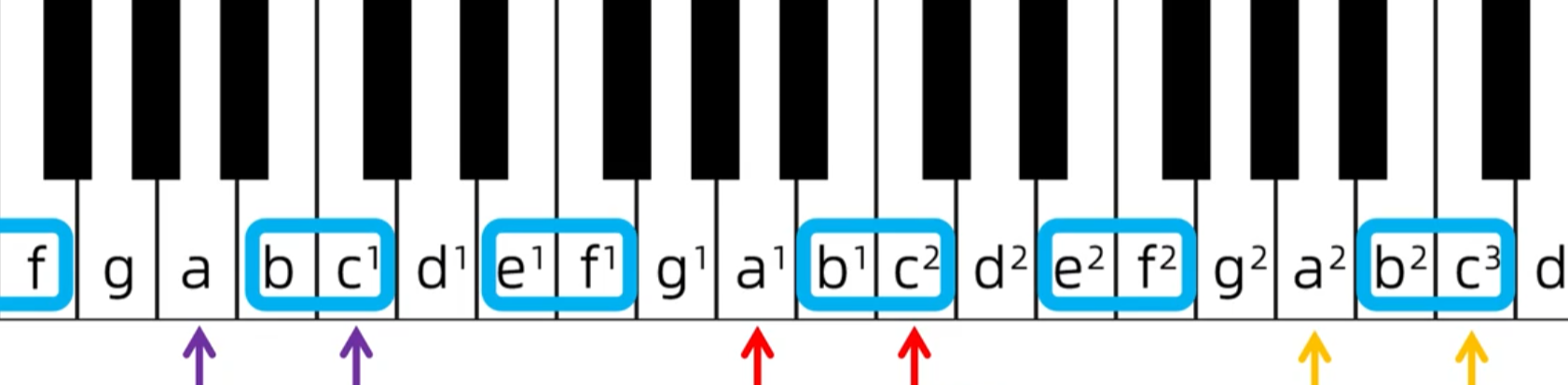
下图就不是a-c是c-a,默认左低右高
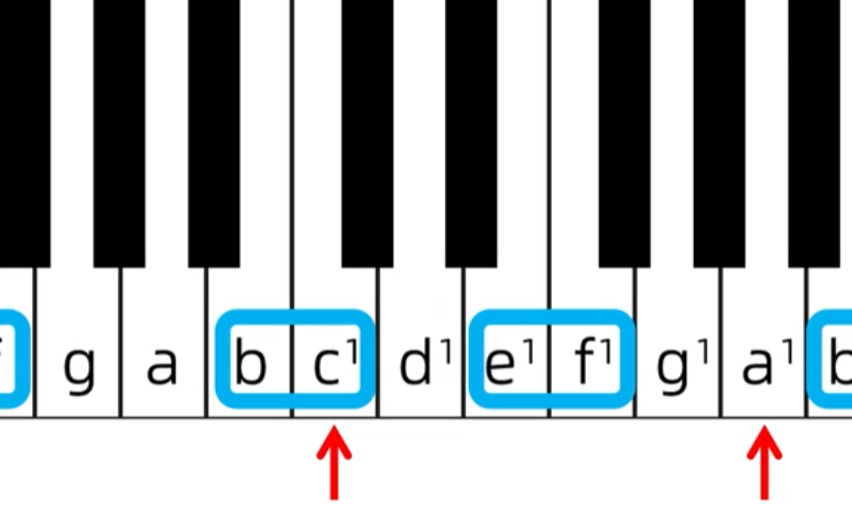
四度:

纯四度:
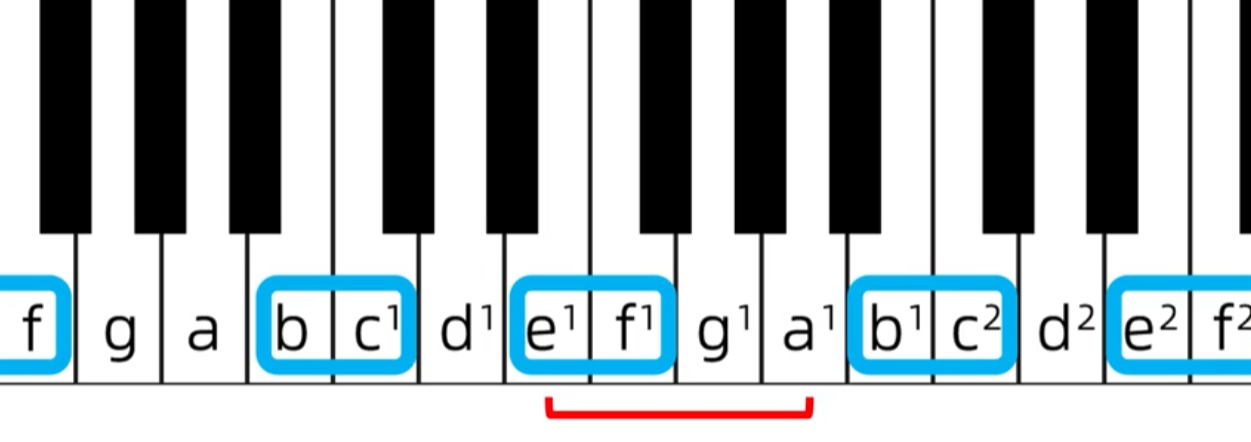
增四度:
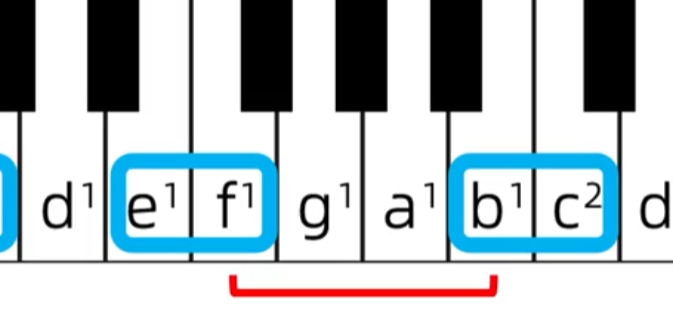
纯四度:
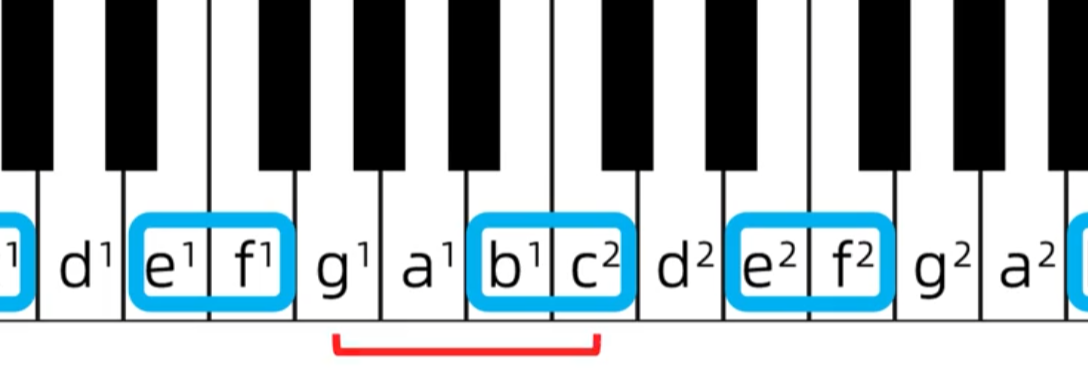
不涉及升降号的时候四度是比较简单的
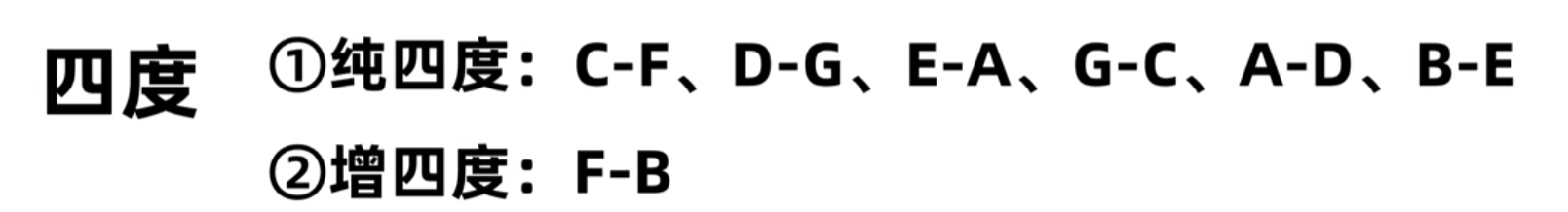
五度:

纯五度:
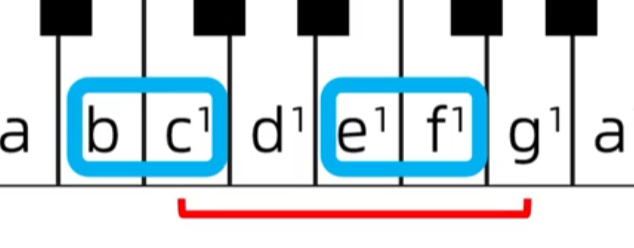
纯五度:
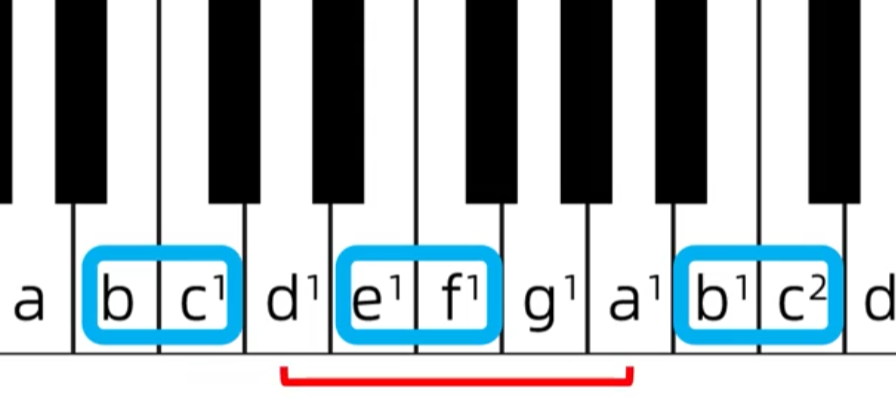
纯五度:
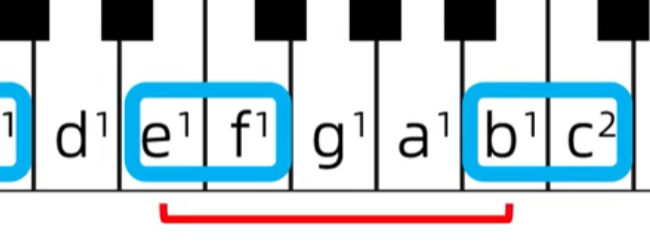
纯五度:
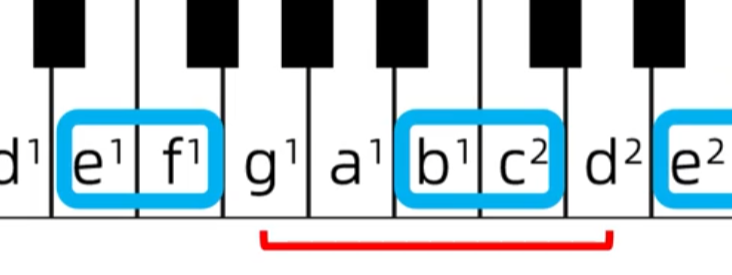
纯五度:
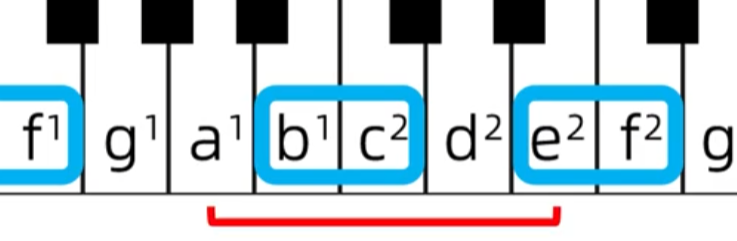
减五度:包含了b-c和e-f
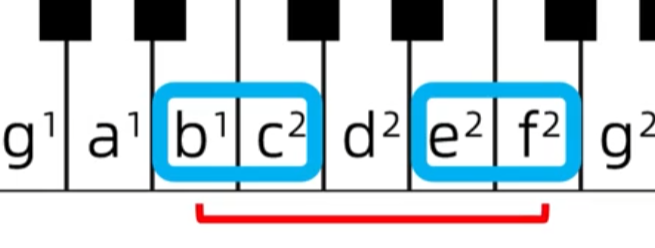
不涉及升降号的五度:
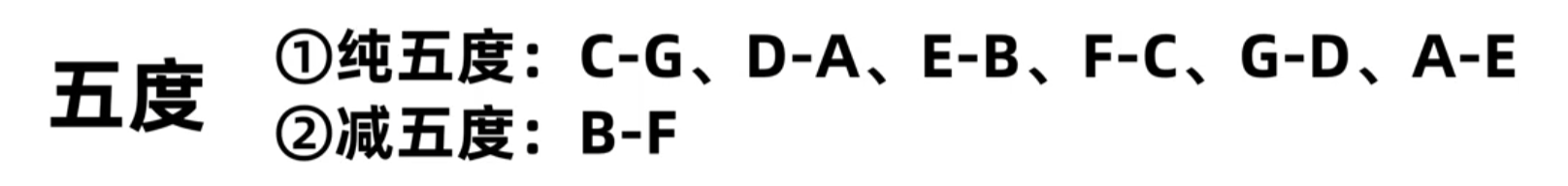
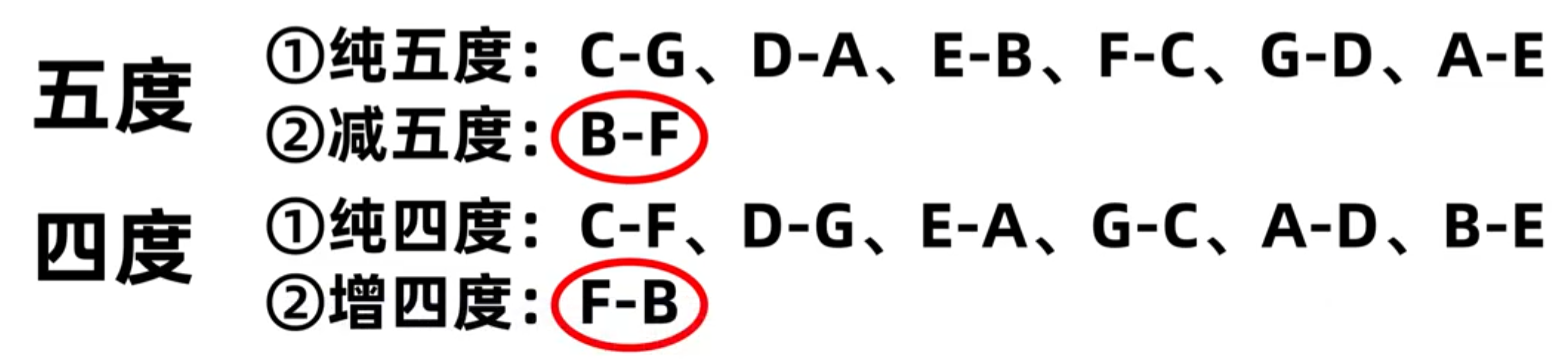
四度和五度:五度是b-f特殊,四度是f-b特殊,所以除了它俩其它的都是纯,可以快速认识
六度和七度

a-f:距离小
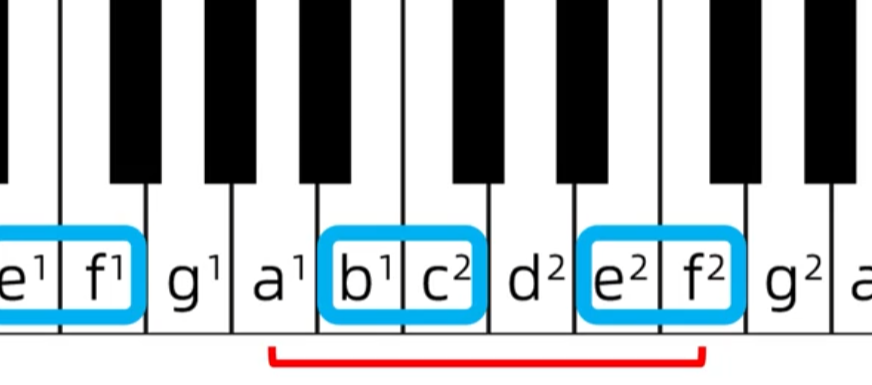
d-b只包含e-f没有包含b-c所以它的距离大,所以它是大六度
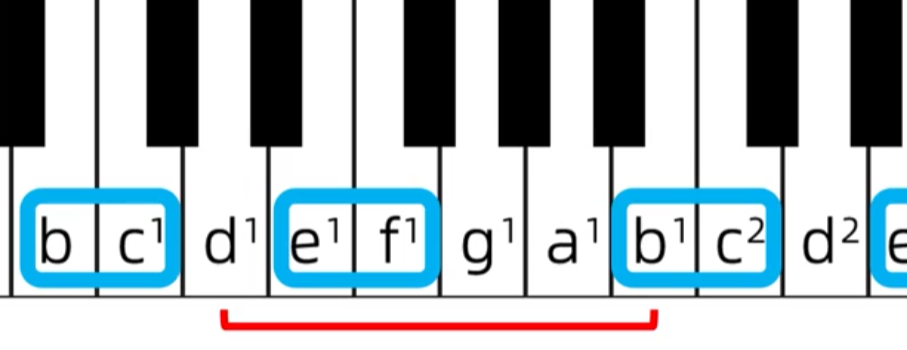
e-d距离小,所以是小七度
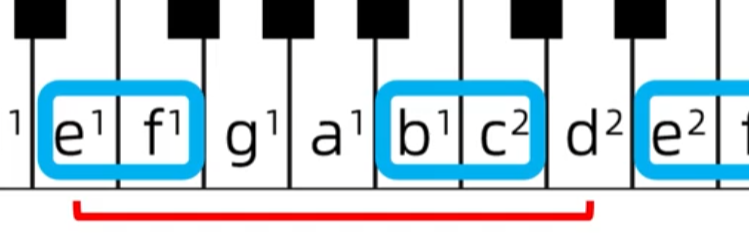
c-b距离长,所以是大七度
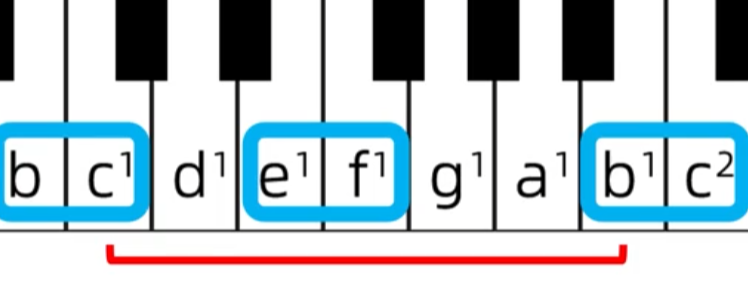
八度:在不涉及升降号的时候它只能是纯八度
总结表:
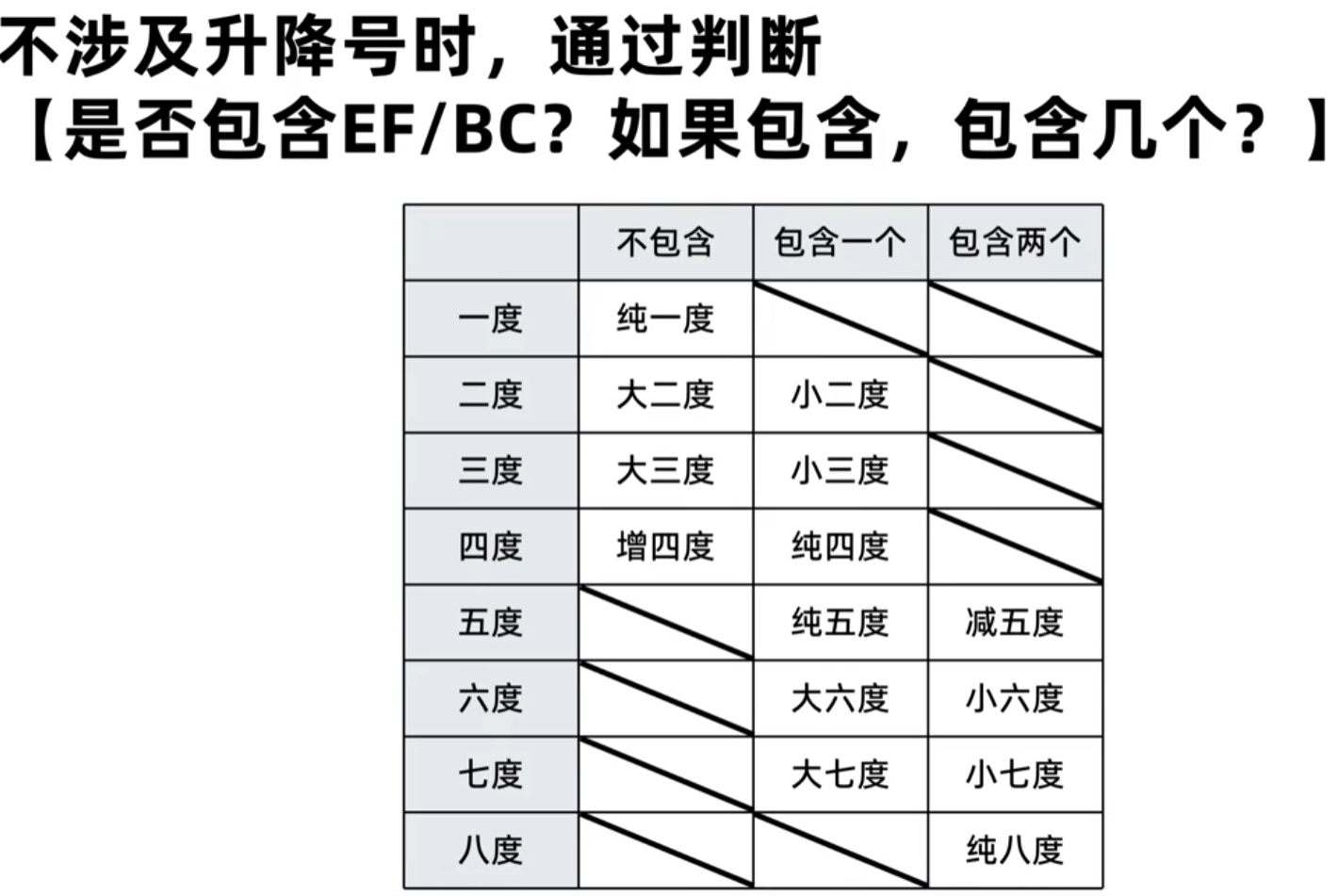
练习:

这篇关于131.乐理基础-快速识别音程(一)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








