自动驾驶（五十五）---------四解轨迹规划

      前面已经三次讲过轨迹规划，还是如隔靴搔痒，诗不着题。所以想少一些理论，多一些实践的角度写轨迹规划，就从常见的场景展开：

1. 问题引入：

       已知条件 车身传感器：车速、Yawrate、方向盘转角；车身周围车辆信息；车道线信息；一个模糊的目标点。求 一条轨迹能到达目标点的位置和角度，轨迹要满足车辆运动学，舒适性，避障等要求。

       怎么理解模糊的目标点？目标位置和角度不是很精确，目标状态的位置和角度随着不断地靠近，可能会不断的收敛，例如十字路口转弯，在转弯过程中摄像头看不到入口的车道线，高精地图只能给出大概的位置和角度，在这样模糊的信息下，需要先规划出一条车道线，引导车辆转弯，在过程中看到车道线，不断收敛目标点的位置和方向。

2. 解决思路:

1. 初始化：初始轨迹规划采用选取多个关键点，利用三次样条曲线生成轨迹。
2. 更新：车身定位采用Klaman滤波收敛，考虑车身的状态和舒适性，结合收敛的目标位置和角度，重新生成三次样条曲线。
3. 输出：利用生成的三次样条曲线，选取一定长度的轨迹，生成轨迹多项式（三次）,满足舒适性；
4. 错误处理：一旦车身偏离轨道，或者目标的位置和状态达不到，需要一套逻辑处理，或者直接退出轨迹规划模式。

3. 三次样条差值：

      在车辆控制中，要通过n个点，为了满足舒适性要求，一般是当前点角度为零作为约束，即b0=0，，最后一个点一般也有角度要求：bn = p；输出为同一坐标系下的分段三次函数。具体推导过程省略，主要讲实现思路：

       1.  已知n个点： 

       2. 分段三次函数表示为：；

           假设： ；

       3. 通过对分段函数本身、一阶导、二阶导在分段点上的连续性，联立方程组，解方程组从而求出分段函数的系数：

       4. 首位一般有约束，即开始点一阶导为车身yawrate下对应的横摆角，即保持当前车身的变化姿势，即使归0也可能不舒适，也可以描述为开始点的二阶导为0。

       5. 末位也有类似的约束，二阶导为0。

       6. 则通过二阶导可以组成以下方程组：

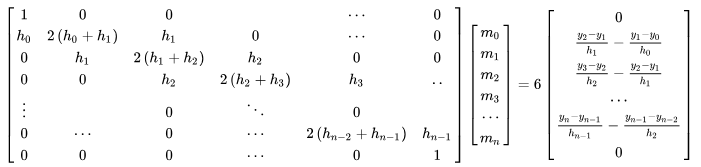
        7. 最后通过以下关系求出其他系数：

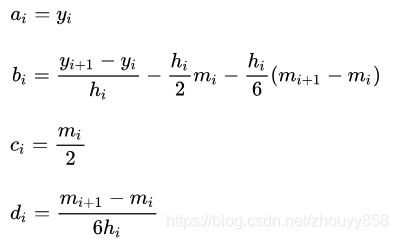
        8. 封装好的c++代码：

struct poly_coef {float c0;float c1;float c2;float c3;/* data */
};//自然边界的三次样条曲线函数
void cubic_getval(vector<Point2f> pxy, vector<poly_coef> opcs) {int n = pxy.size();float* ai = (float*)malloc(sizeof(float) * (n-1));float* bi = (float*)malloc(sizeof(float) * (n-1));float* ci = (float*)malloc(sizeof(float) * (n-1));float* di = (float*)malloc(sizeof(float) * (n-1));float* h = (float*)malloc(sizeof(float) * (n-1));  //x的??/* M矩阵的系数*[B0, C0, ...*[A1, B1, C1, ...*[0,  A2, B2, C2, ...*[0, ...             An-1, Bn-1]*/float *A = (float *)malloc(sizeof(float) * (n - 2));float *B = (float *)malloc(sizeof(float) * (n - 2));float *C = (float *)malloc(sizeof(float) * (n - 2));float *D = (float *)malloc(sizeof(float) * (n - 2)); //等号右边的常数矩阵float *E = (float *)malloc(sizeof(float) * (n - 2)); //M矩阵float *M = (float *)malloc(sizeof(float) * (n)); //包含端点的M矩阵//计算x的步长for (int i = 0; i < n - 1; i++){h[i] = pxy[i + 1].x - pxy[i].x;}//指定系数for (int i = 0; i < n - 3; i++){A[i] = h[i]; //忽略A[0]B[i] = 2 * (h[i] + h[i + 1]);C[i] = h[i + 1]; //忽略C(n-1)}//指定常数Dfor (int i = 0; i < n - 3; i++) {D[i] = 6 * ((pxy[i + 2].y - pxy[i + 1].y) / h[i + 1] - (pxy[i + 1].y - pxy[i].y) / h[i]);}//求解三对角矩阵，结果赋值给ETDMA(E, n - 3, A, B, C, D);M[0] = 0;     //自然边界的首端M为0M[n - 1] = 0; //自然边界的末端M为0for (int i = 1; i < n - 1; i++) {M[i] = E[i - 1]; //其它的M值}//?算三次?条曲?的系数for (int i = 0; i < n - 1; i++) {opcs[i].c0 = map[n + i];opcs[i].c1 = (map[n + i + 1] - map[n + i]) / h[i] - (2 * h[i] * M[i] + h[i] * M[i + 1]) / 6;opcs[i].c2 = M[i] / 2;opcs[i].c3 = (M[i + 1] - M[i]) / (6 * h[i]);}free(h);    free(A);free(B);    free(C);free(D);    free(E);free(M);    free(ai);free(bi);    free(ci);free(di);
}void TDMA(real_T *X, const int_T n, real_T *A, real_T *B, real_T *C, real_T *D){float tmp;//上三角矩阵C[0] = C[0] / B[0];D[0] = D[0] / B[0];for (int i = 1; i < n; i++) {tmp = (B[i] - A[i] * C[i - 1]);C[i] = C[i] / tmp;D[i] = (D[i] - A[i] * D[i - 1]) / tmp;}//直接求出X的最后一个值X[n - 1] = D[n - 1];//逆向迭代， 求出Xfor (int i = n - 2; i >= 0; i--){X[i] = D[i] - C[i] * X[i + 1];}
}

4. 生成轨迹

        由于上一步选点，生成分段三次曲线，能不能直接把0点对应的三次曲线作为轨迹线输出呢？我认为不行，首先，生成的分段函数长度是由分段点决定的，不一定满足要求；再次，两帧之间是强调拟合，没有考虑其舒适性和车辆运动学模型。因此我们需要重新拟合当前场景下合适的轨迹线。

        传统方法多项式拟合是最小二乘法拟合，前面有专门的的文章介绍带约束的最小二乘法，这里我也附上一般的最小二乘法opencv代码：       

bool curveFitting(CvSeq* inDataSet, float curveParam[4])
{if(!inDataSet)return false;int dataSetSize = inDataSet->total;//系数矩阵存储位置CvMat* cMatrix = cvCreateMat(4, 4, CV_32FC1);cvZero(cMatrix);//常量系数矩阵CvMat* cstMatrix = cvCreateMat(4, 1, CV_32FC1);cvZero(cstMatrix);//(0, 0)*((float*)CV_MAT_ELEM_PTR(*cMatrix, 0, 0)) = static_cast<float>(dataSetSize);CvPoint2D32f* sample = 0;float x = x2 = x3 = x4 = x5 = x6 = y = 0.f;for(int i = 0; i < dataSetSize; ++i){sample = (CvPoint2D32f*)cvGetSeqElem(inDataSet, i);x = sample->x;x2 = x * x;x3 = x2 * x;x4 = x3 * x;x5 = x4 * x;x6 = x5 * x;*((float*)CV_MAT_ELEM_PTR(*cMatrix, 0, 1)) += x; *((float*)CV_MAT_ELEM_PTR(*cMatrix, 0, 2)) += x2;*((float*)CV_MAT_ELEM_PTR(*cMatrix, 0, 3)) += x3;*((float*)CV_MAT_ELEM_PTR(*cMatrix, 1, 3)) += x4;*((float*)CV_MAT_ELEM_PTR(*cMatrix, 2, 3)) += x5;*((float*)CV_MAT_ELEM_PTR(*cMatrix, 3, 3)) += x6;y = sample->y;*((float*)CV_MAT_ELEM_PTR(*cstMatrix, 0, 0)) += y;*((float*)CV_MAT_ELEM_PTR(*cstMatrix, 1, 0)) += y * x;*((float*)CV_MAT_ELEM_PTR(*cstMatrix, 2, 0)) += y * x2;*((float*)CV_MAT_ELEM_PTR(*cstMatrix, 3, 0)) += y * x3;}*((float*)CV_MAT_ELEM_PTR(*cMatrix, 1, 0)) = *((float*)CV_MAT_ELEM_PTR(*cMatrix, 0, 1));*((float*)CV_MAT_ELEM_PTR(*cMatrix, 1, 1)) = *((float*)CV_MAT_ELEM_PTR(*cMatrix, 0, 2));*((float*)CV_MAT_ELEM_PTR(*cMatrix, 1, 2)) = *((float*)CV_MAT_ELEM_PTR(*cMatrix, 0, 3));*((float*)CV_MAT_ELEM_PTR(*cMatrix, 2, 0)) = *((float*)CV_MAT_ELEM_PTR(*cMatrix, 0, 2));*((float*)CV_MAT_ELEM_PTR(*cMatrix, 2, 1)) = *((float*)CV_MAT_ELEM_PTR(*cMatrix, 1, 2));*((float*)CV_MAT_ELEM_PTR(*cMatrix, 2, 2)) = *((float*)CV_MAT_ELEM_PTR(*cMatrix, 1, 3));*((float*)CV_MAT_ELEM_PTR(*cMatrix, 3, 0)) = *((float*)CV_MAT_ELEM_PTR(*cMatrix, 0, 3));*((float*)CV_MAT_ELEM_PTR(*cMatrix, 3, 1)) = *((float*)CV_MAT_ELEM_PTR(*cMatrix, 1, 3));*((float*)CV_MAT_ELEM_PTR(*cMatrix, 3, 2)) = *((float*)CV_MAT_ELEM_PTR(*cMatrix, 2, 3));CvMat* pcMatrix = cvCreateMat(4, 4, CV_32FC1);cvZero(pcMatrix);CvMat result = cvMat(4, 1, CV_32FC1, curveParam);cvZero(&result);cvInvert(cMatrix, pcMatrix, CV_LU);cvMatMul(pcMatrix, cstMatrix, &result);cvReleaseMat(&pcMatrix);cvReleaseMat(&cstMatrix);return true;
}

        同样的多项式拟合没有考虑帧间的舒适性，也没有考虑车辆运动学，所以我们需要新的思路解决问题。这里我介绍一种物理含义解决以上问题，如图：

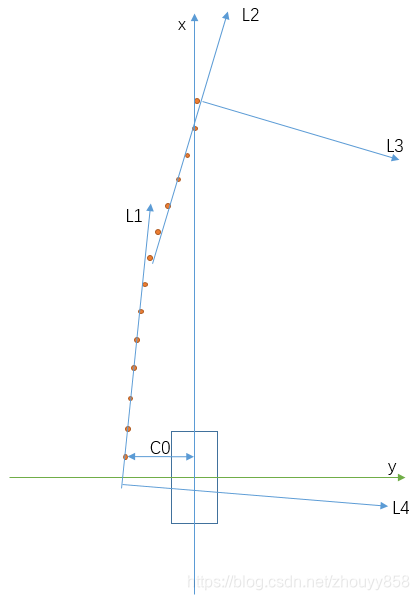
        图示：L1为前面几个点拟合的直线，C0为车中心到L1的距离，L2为最后几个点拟合的直线，L3为L2的法线，L4为L1的法线，计算L3和L4的交点。

        对于以上点得到的轨迹多项式  y=a+bx+cx^2+dx^3，其中c直接为C0，b是L1的角度，c是 L3和L4的圆的半径倒数，d是c的变换率，一般在中间在选一组点，计算c的变化率。

5. 优化更新

        上面生成的轨迹，没有考虑舒适性和车辆运动学模型。在保证舒适性的方法中，窗口滤波是最直接和简单的方法，但是有明显的确定，产生延迟。这里介绍一种新的思路，供大家思考。

1.  我们把上一帧计算的轨迹离散成一串点。
2.  通过本次车身姿态和位置变化，仿射变换计算出上一帧轨迹离散点。
3.  对新观察的离散点，和上一帧推算的离散点进行Kalman滤波。
4.  对滤波结果安装第4步重新计算新的轨迹。

6. 错误检测

       对输出的轨迹进行检测，对计算的C0、C1、C2、C3进行数值约束。对不满足要求的结果进行退出操作