本文主要是介绍Peter算法小课堂—动态规划,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Peter来啦,好久没有更新了呢
今天,我们来讨论讨论提高组的动态规划。
动态规划
动态规划有好多经典的题,有什么背包问题、正整数拆分、杨辉三角……但是,如果考到陌生的题,怎么办呢?比如说2000年提高组的乘积最大、石子合并……,所以说,我们要理解动态规划的本质。

那么,我们动态规划的第一步就是状态定义

dp的第二步就是填表格、写状态转移方程。

最后一步就是根据状态转移方程写代码了。其实,我觉得,dp最难的地方就是第二步,其次就是根据递推式写代码。给大家练一练根据递推式写代码吧。
递推1

那么,代码很简单,长这样👇
#include<bits/stdc++.h>
using namespace std;
int f[110][1010],n,v,c[110],w[110];
int main()
{scanf("%d%d",&v,&n);for (int i=1;i<=n;++i)scanf("%d%d",&c[i],&w[i]);for (int i=1;i<=n;++i) {for (int j=1;j<c[i];++j)f[i][j]=f[i-1][j];for (int j=c[i];j<=v;++j)f[i][j]=max(f[i-1][j],f[i-1][j-c[i]]+w[i]);}printf("%d\n",f[n][v]);return 0;
}再来一道题
递推2

代码长这样
#include<bits/stdc++.h>
using namespace std;
int f[1010],n,c[1010];
int main()
{scanf("%d",&n);for (int i=1;i<=n;++i)scanf("%d",&c[i]);for (int i=1;i<=n;++i)for (int j=1;j<=i;++j)f[i]=max(f[i],f[i-j]+c[j]);int k,x;scanf("%d",&k);for (int i=1;i<=k;++i) {scanf("%d",&x);printf("%d\n",f[x]);}return 0;
}递推练完了,就要练习状态转移方程了(靠自觉)
摆花
原题链接:P1077 [NOIP2012 普及组] 摆花 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
那么这道题,我们把题意抽象化成:有 n 个数(c1,c2,...,cn),0⩽ci⩽ai,求有多少种方案数使。
首先,看到这道题,我给出5种办法,分别对应初学者、普及Oler、不大聪明的提高Oler、灰常聪明的提高Oler。
初学者
最最最简单的办法就是搜索+记忆化
#include<bits/stdc++.h>
using namespace std;
const int maxn=105, mod = 1000007;
int n, m, a[maxn], rmb[maxn][maxn];
int dfs(int x,int k)
{if(k > m) return 0;if(k == m) return 1;if(x == n+1) return 0;if(rmb[x][k]) return rmb[x][k]; //搜过了就返回int ans = 0;for(int i=0; i<=a[x]; i++) ans = (ans + dfs(x+1, k+i))%mod;rmb[x][k] = ans; //记录当前状态的结果return ans;
}
int main()
{cin>>n>>m;for(int i=1; i<=n; i++) cin>>a[i];cout<<dfs(1,0)<<endl;return 0;
}搜索所有可能的并且记忆化。
普及Oler
其次,应该会想到动态规划了。

时间复杂度大大降低,给出代码
#include <bits/stdc++.h>
using namespace std;
const int N=109;
const int MOD=1e6+7;
int f[N][N],a[N],n,m;
int main(){cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i];f[0][0]=1;for(int i=1;i<=n;i++){for(int j=0;j<=m;j++){if(j-1<a[i])f[i][j]=(f[i-1][j]%MOD+f[i][j-1]%MOD)%MOD;else f[i][j]=(f[i-1][j]%MOD+f[i][j-1]%MOD-f[i-1][j-1-a[i]]%MOD+MOD)%MOD;}}cout<<f[n][m]<<endl;return 0;
}还是比较蒟蒻的
不大聪明的提高Oler
再其次,就是前缀和优化,大家都学过,给出代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 105, mod = 1000007;
int n, m, f[maxn], sum[maxn], a[maxn];
int main(){cin>>n>>m;for(int i=1; i<=n; i++) cin>>a[i];f[0] = 1;for(int i=0; i<=m; i++) sum[i] = 1;for(int i=1; i<=n; i++){for(int j=m; j>=1; j--){int t = j - min(a[i], j) - 1;if(t < 0) f[j] = (f[j] + sum[j-1])%mod;else f[j] = (f[j] + sum[j-1] - sum[t] + mod)%mod;}for(int j=1; j<=m; j++) sum[j] = (sum[j-1] + f[j])%mod;}cout<<f[m]<<endl;return 0;
}来了,它又来了,它就是我们的生成函数!!!
灰常聪明的提高Oler
生成函数啊啊啊
大家如果不会生成函数的话,可以康康这位大佬的博客生成函数(母函数)——目前最全的讲解-CSDN博客
我们构造一个函数,其中
项的系数即为答案。可以做n-1次NTT,然后输出。时间复杂度:
。这里我不给出代码了。
其实,也不用算出乘积,有一种更好的方法
我们约定,
,
若, 则
,其中
,懂得都懂
这一题比较难,来一道简单亿点的题
参差不齐
n名电影演员依次排成一排,第i人的颜值为y[i],有些参差不齐。你希望挑选m个人拍一张电影海报,这m个人的前后顺序不能发生变化。你希望挑选的这排演员相邻的颜值不能相差太大,于是你定义颜值的参差不齐程度为相邻两人颜值差距的绝对值之和。求这m人的参差不齐程度最少是多少?
这一题最难的是状态定义,要是状态定义完成了的话,状态转移方程就显而易见了。
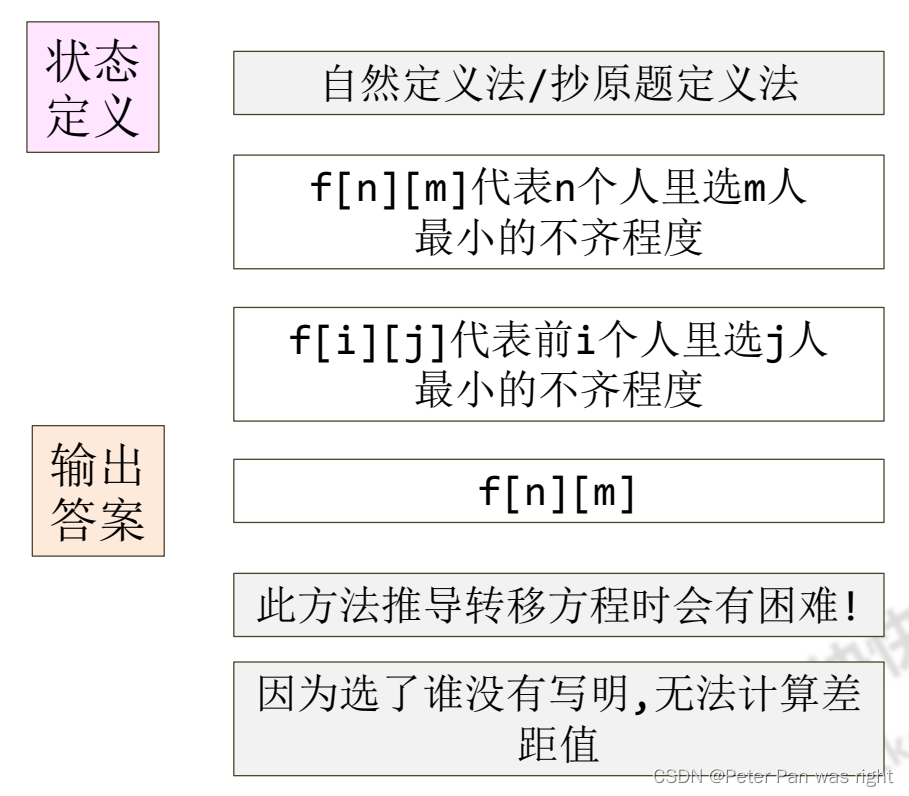
这个定义不太好,下面给出正确的定义及代码
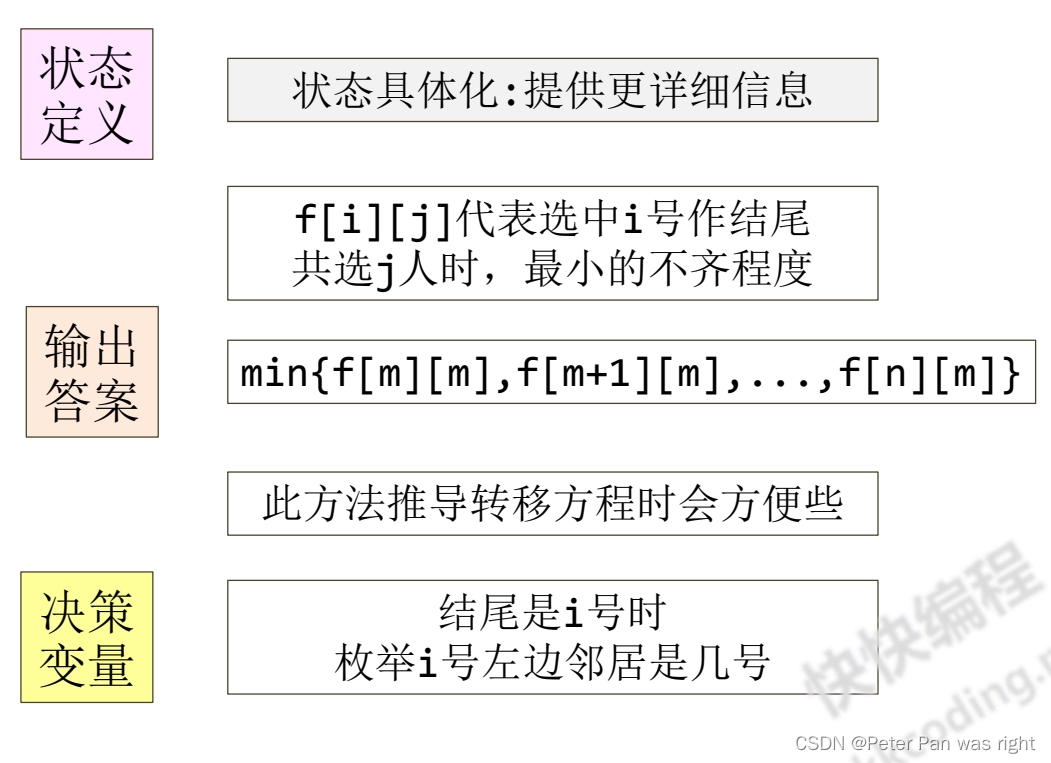
下面给出代码👇
for(int i=1;i<=n;i++) f[i][1]=0;
for(int j=2;j<=m;j++)//枚举j代表选中人数for(int i=j;i<=n;i++){//枚举i代表结尾编号f[i][j]=INF;for(int k=j-1;k<i;k++)//结尾是i号时枚举k代表i号的左边邻居是几号f[i][j]=min(f[i][j],f[k][j-1]+abs(y[i]-y[k]));}
int ans=INF;
for(int i=m;i<=n;i++) ans=min(ans,f[i][m]);
cout<<ans<<endl;乘积最大
原题链接:P1018 [NOIP2000 提高组] 乘积最大 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
这题显然是一道数位dp
状态定义:f[i][j] 表示前 i 位数包含 j 个乘号所能达到的最大乘积
easy代码:
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
long long f[45][60];
string in;
int n,k;//n位数 k个乘号
long long g[45];
long long cut(int l,int r){long long end = 0;for(int i = l;i <= r;i++)end = end * 10 + g[i];return end;
}
int main(){cin >> n >> k >> in;for(int i = 1;i <= n;i++)g[i] = in[i - 1] - '0';for(int i=1;i<=n;i++)f[i][0] = cut(1,i);for(int i = 2;i <= n;i++){ //枚举分割为前i位数字 for(int a = 1;a <= min(i-1,k);a++){ //枚举有几个乘号 for(int b = a;b < i;b++){ //在第几位放乘号 f[i][a] = max(f[i][a],f[b][a-1] * cut(b + 1,i));}}}cout<<f[n][k];return 0;
}然后,就是我们的毒瘤最后一题啦
面条切割
这一题涉及到动态规划的本质,但是这一题要用到微积分,所以……
原题链接:Problem - 5984 (hdu.edu.cn)
设长度为x的面条期望为f(x)。显然,当x<d时,f(x)=0。当x>b时,设t为0~x上的坐标值,吃掉t~x上的面条,剩下的面条就是0~t,即吃掉剩下的面条次数期望为f(t) 。dt为一个很小的线元,点落在dt上的概率为,而dt贡献的期望为:dt的长度为t,如上所述,贡献了f(t)的期望。最后我们再把这些相加(积分),得到
。接下来就是解出f(x)了。我们可以对f(x)求个导,然后还原,如下(LateX难打)
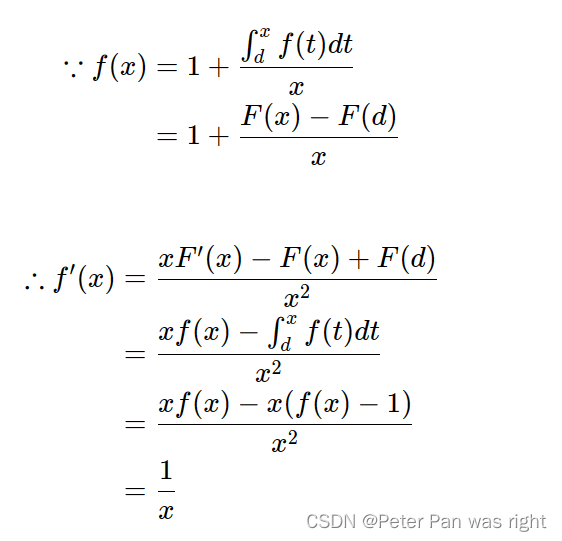
于是乎,。然后,我们代一个特指进去,随便哪一个都行,最好是x=d,然后得到
。综上所述,
。代码来啦
#include <bits/stdc++.h>
using namespace std;
int main() {int T;cin >> T;while (T--) {double a, b;cin >> a >> b;if (a <= b)cout << "0.000000" << endl;elsecout << fixed << setprecision(6) << 1.0 + log(a / b) << endl;}return 0;
}时间复杂度几乎为O(1)!
OK!今天就讲到这里,886
这篇关于Peter算法小课堂—动态规划的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



