[行人重识别论文阅读]Person Re-identification by Contour Sketch under Moderate Clothing Change

论文地址： https://arxiv.org/abs/2002.02295
论文代码： 没有官方代码，准备日后复现，先空在这里

本文思想

去除掉行人的衣服特征，利用行人的轮廓来识别行人。

但是这样就会产生一个问题就是不同行人之间的轮廓太为相似，所以我们必须在使用全局轮廓图的同时将轮廓图的局部信息引入。但是我们又如何充分的利用局部信息呢？方法如下图所示：

如上图(b)我们以轮廓图的中心为极点，通过不断的变化θ与r来扫描到整个人的所有轮廓信息。

整体流程图

具体方法

SPT

我们将RGB图像进行空间极性变化的方法叫做SPT。
那么具体是如何变化的？
首先应该知道极性变化的定义：

所以我们就知道要想将sketch(轮廓图）以极坐标的方式变为直角坐标下的点，那么就是不断的变化θ与R就能得到轮廓中的每一个点。而我们现在研究的是怎么控制θ与R能充分挖掘到所有的局部信息。

本文提出了N个变化角度以及M个变化半径

N个角度:

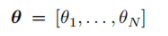
这N个变换角度是在一定角度范围内的N个值，比如是-pai 到pai的N等份值，当然不一定是平均等份，也可能是不均匀分配，后面会提到如何分配

M个变化半径:

θ的变化毫无疑问，但是为什么R也要使用变化范围呢？

因为不同的人具有不同的体型，如果R不变化，比如就固定的R长度不同的角度去扫描一圈后，瘦的人可能特征扫描一部分，而胖人的特征压根就没有扫描到。所以我们就使用定义了M个变化半径 以M*N的组合方式对整个sketch进行一次扫描

假设我们设定了Rmax（在论文里设为2），那么M个变换半径就是0-2的M等份(而j的范围自然属于（1-M）中的所有整数）

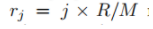
我们从上面知道了通过角度和半径的变化能够得到身体的轮廓特征信息，并且N与M越大自然得到的特征信息会更多，但是如果分的太细会导致计算量过大反而导致计算的效率低下，所以N和M的选取十分的重要，作者针对该问题提出了优化N个角度的方法：

优化方法:

为了使采样角θi保持在一定的范围内和一定的顺序，我们使用下述公式
(λk是我们定义的一个参数，在一开始的时候λk是一个常量，所以刚开始的角度是均匀分布的，之后我们在训练期间不断的更新λk的变化，得到了一个非均匀变化的角度，与前文所说的θ不平均取得相呼应）

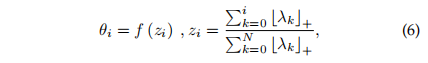
zi可以相当于整个角度的几等分点，通过不断优化该分点，就相当于优化角度的选择，同时由于(6)中zi公式计算的特性， 我们会保证前面的zi小于后面的zi，而下述的(7)又可以将θi的范围控制到(a,b),这样既满足了范围的要求又满足了顺序的要求。

ASE

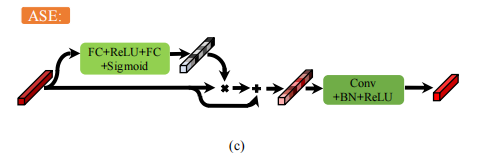
如上图所示，其实这个ASE就是一个对通道加attention的过程（图中虽然没有看出是对channel加attention，但原文明确说了是对channel加attention），无需多言。

整体流程-stream部分

前文我描述了通过引入N个角度，M个变化半径来充分的扫描sketch，但是开头我们就说过，每个图整体sketch太像了，不容易分辨，所以我们又同时引入了两个其它角度，作为局部特征与全局特征共同学习。

这样我们就可以将原图分为三个stream（本文规定是三个stream）分别计算

下图即为此篇论文的三个stream角度选择：

损失函数

1.对每个流的每个分支做（softmax+交叉熵损失）即传统的分类损失
2.对三个分支得到的所有特征做三元组损失
3.最终损失表达式

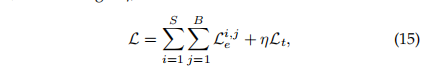
理解参考

本文思想理解大多来自https://zhuanlan.zhihu.com/p/361586179