对keras.permute_dimensions和numpy.transpose空间维度转置过程的理解（Axis的理解）

keras.permute_dimensions和numpy.transpose，这两个函数的作用是对矩阵进行维度的转置， 具体请参考官方文档，这里只给出矩阵维度转置是怎么理解的？

1. 写在前面

今天遇到一个时间序列分析的任务，使用了Attention机制，看代码之后，有几个空间转置的过程其实有点懵。

所以通过查资料理解了一下空间维度转置，顺便理解了一下三维矩阵的沿着某一个轴的加法，我把自己的理解技巧记录下来，不一定适合每个人，但是如果这样看待转置问题的话，应该知道具体是怎么变的一个过程。

如果你还没明白我说啥，那么我可以举个例子：

A=np.arange(12).reshape([2,3,2])
X=tf.transpose(A,[0,2,1])
Y=tf.transpose(A,[1,0,2])

通过这三行代码，你能一下子反应出X和Y的形状和具体的数值吗？

如果不能，那么我告诉你结果：

A长这个样子， 是一个[2, 3, 2]的三维矩阵

[[[ 0  1][ 2  3][ 4  5]][[ 6  7][ 8  9][10 11]]]

X是把A的后两个维度进行了转置， X的大小：[2,2,3]， 长这个样子：

[[[ 0  2  4][ 1  3  5]][[ 6  8 10][ 7  9 11]]]

Y是把A的前两个维度进行了转置，Y的大小:[3,2,2]， 长这个样子：

[[[ 0  1][ 6  7]][[ 2  3][ 8  9]][[ 4  5][10 11]]]

我们可以发现，判断三维矩阵转置后的形状还是比较好判断的， 无非就是原来的维度大小，转换对应即可。 但是具体的样子我们理解是怎么变过去的吗？

并且如果我两个三维矩阵相加的时候，你能一下子反应出axis=0， 1， -1都是在哪个维度上进行拼接的吗？

 # 三维数组  t3 = tf.constant([[[1, 2], [2, 3]], [[4, 4], [5, 3]]])t4 = tf.constant([[[7, 4], [8, 4]], [[2, 10], [15, 11]]])with tf.Session() as sess:# 三维数组针对 axis 为0 和 1 和 -1 的情况print(sess.run(tf.concat([t3, t4], 0)))print(sess.run(tf.concat([t3, t4], 1)))print(sess.run(tf.concat([t3, t4], -1)))

这两个就是我今天分享的，应该怎么理解这个转置的过程和拼接的过程。我这里分享一下我的理解方法，我是通过固定数据，转换视角来理解的， 下面具体说说是什么意思？

2. 三维？ 我们还是先从二维来来理解

对于二维矩阵的转置，我相信肯定大家都理解是怎么转的， 比如下面的例子：

A = np.array([[1, 2, 3], [4, 5, 6]])
X = tf.transpose(A, [1, 0])      # 这个地方其实是0维和1维进行了交换

这个我们很容易就会得出答案， A的转置矩阵就是：
[[1 4]
[2 5]
[3 6]]

这个应该大家都会做，但是具体的转变过程，可能我们每个人理解的就不一样了，可能有的人是固定轴，变数字，也有的人固定数字，转变轴。 我就是后者，我对于二维转置问题是这样理解的， 对于二维矩阵来说，我们知道会有axis=0, axis=1两个轴，如果你经常使用numpy和pandas的话，对我说的这一点肯定不陌生，毕竟矩阵拼接， sum加和这些操作都有个axis的属性。 这个其实就是二维矩阵的两个方向，类似x，y轴一般。我的理解是这样子的，横向是axis=1， 纵向是axis=0。

如果你也是这样理解的话，恭喜你，对于二维矩阵的拼接求和，其实就很好理解了，比如np.sum(a, axis=0) 我们很容易就理解这是沿着axis=0的方向加和，结果就是[5, 7, 9]， np.sum(a, axis=1)， 很容易理解是axis=1的方向加和， 结果[6, 15]。 当然np.concat， 还有pandas的拼接操作都是同理。

这两个轴的目的是锁定视角，就是我观察的角度永远是这个角度（axis=0朝下，axis=1朝着右）

那么这种情况下，做转置怎么理解呢？ 我依然是数字不变，观察的角度进行变换， 但是这个观察的角度怎么变的呢？ 依赖于这两个轴。 当然只是轴哈，如果轴有含义的话，比如axis=0方向代表样本， axis=1代表特征这种，含义可不能变，只是变个观察的角度罢了。 啥意思呢？

二维转置，其实就是axis=0和axis=1交换一下位置，然后再回到我axis=0朝下， axis=1朝右的视角下观察这个矩阵， 如下图：

这个转变视角的过程，其实相当于我们人走到了这个矩阵的后面，然后头顺时针旋转90度观察的（你可以发挥空间想象力，想象一下这个过程）。

有人可能有疑问，为啥要这么麻烦，我直接数字变一下子不就完了？ 嗯嗯， 当然可以，哪个好理解用哪个， 我之所以用后者，是因为三维的情况下，变数字可就不是那么好变了， 不信？ 我们就看看三维的情况。

3. 三维下的矩阵转置

我们就看下面这个简单的例子吧：

这是一个[2, 3, 4]大小的矩阵，如果我要问，前两个轴(01)交换，你能一下子反应出下面的这个图片吗？

这个转置对应numpy就是np.transpose(x, (1, 0, 2)),，对应keras就是keras.backend.permute_dimensions(x, (1, 0, 2))。

反正我如果是从变换数字的角度看的话，反应不出后面的结果，即使看了一篇博客的描述，也是得寻思半天。 但是如果数字不变，角度变换的技巧理解的话，这个问题就容易想了。

三维的里面，我依然是借助轴的，只不过这次需要三个，并且0，1， 2的方向得是下面这样子：

并且，三个轴的方向不能变，只能从这个视角看待矩阵，这样的话，我们上面的01轴交换位置，就是这样子：

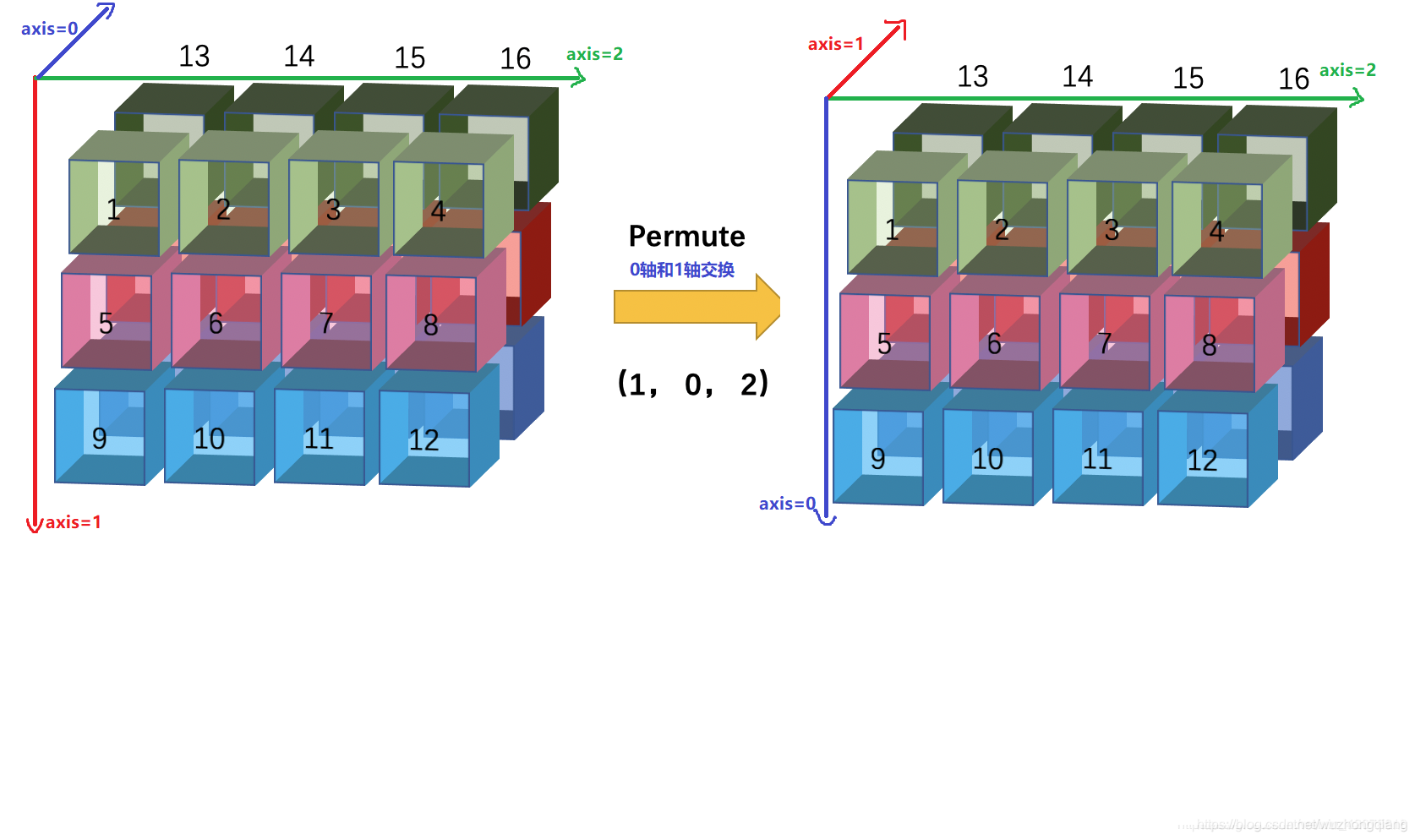
这个时候，就转换角度，想办法让axis=0朝里，axis=1朝下，axis=2朝右， 就相当于从矩阵的后面爬到上面，然后从右往左看就是最终的结果。或者爬到上面，把矩阵沿着axis=2的方向逆序一下子（就相当于朝右了），也是最终的结果。

OK， 如果没懂的话可以再看一个：

这次是后两个轴进行交换，我的理解依然是换坐标轴先，(12)交换，

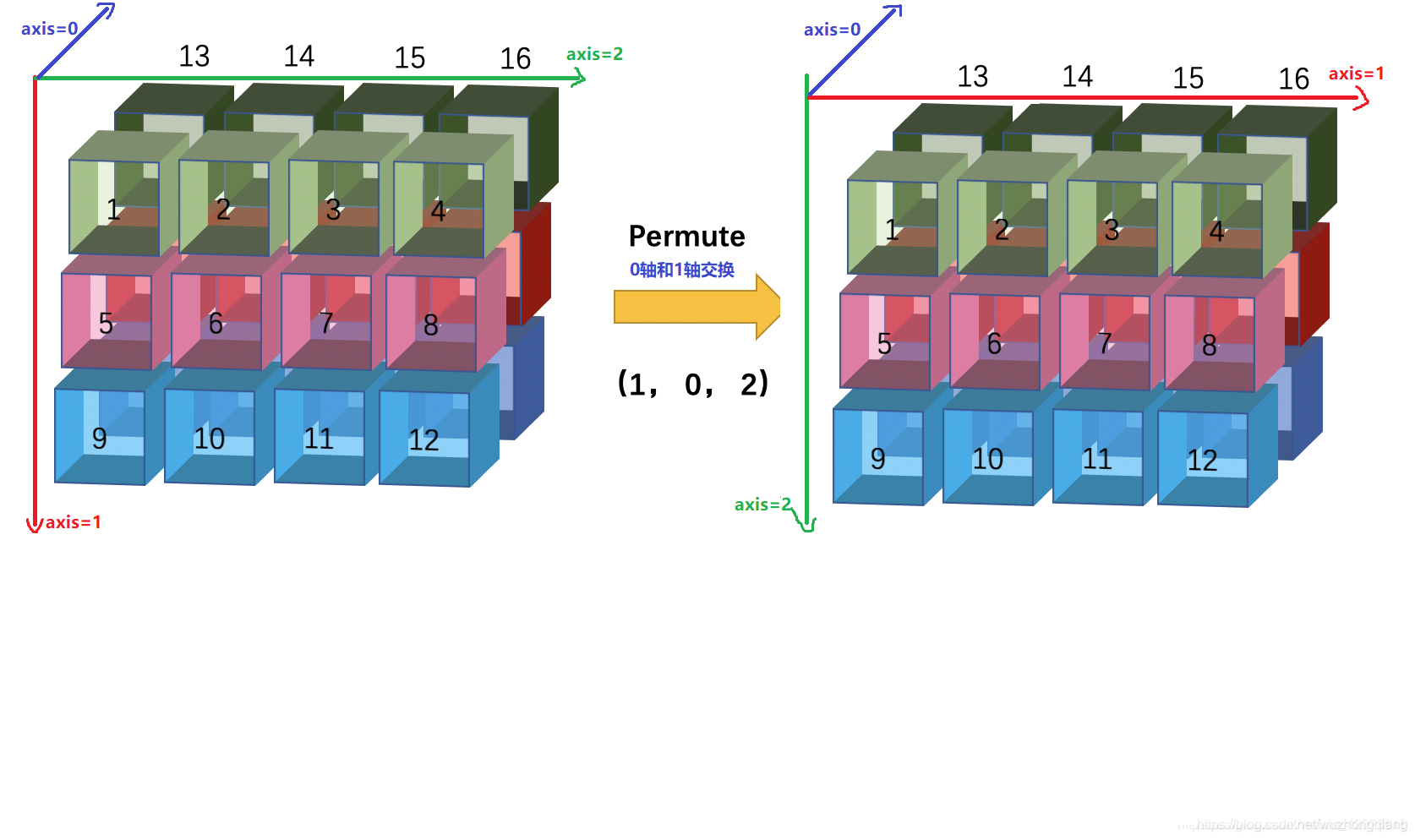
然后同样是想办法换成原来的观察视角（axis=0朝里，axis=1朝下, axis=2朝右）， 即跑到矩阵的后面，然后头顺时针转90度，然后沿着axis=0的方向逆序一下看就是最后的结果。其实说的这么麻烦，只要领悟了这个方式，用空间想象就能够很轻松的想出是怎么变的。

下面这个0和2交换的，就不说了，自己可以标出坐标轴试一下子：

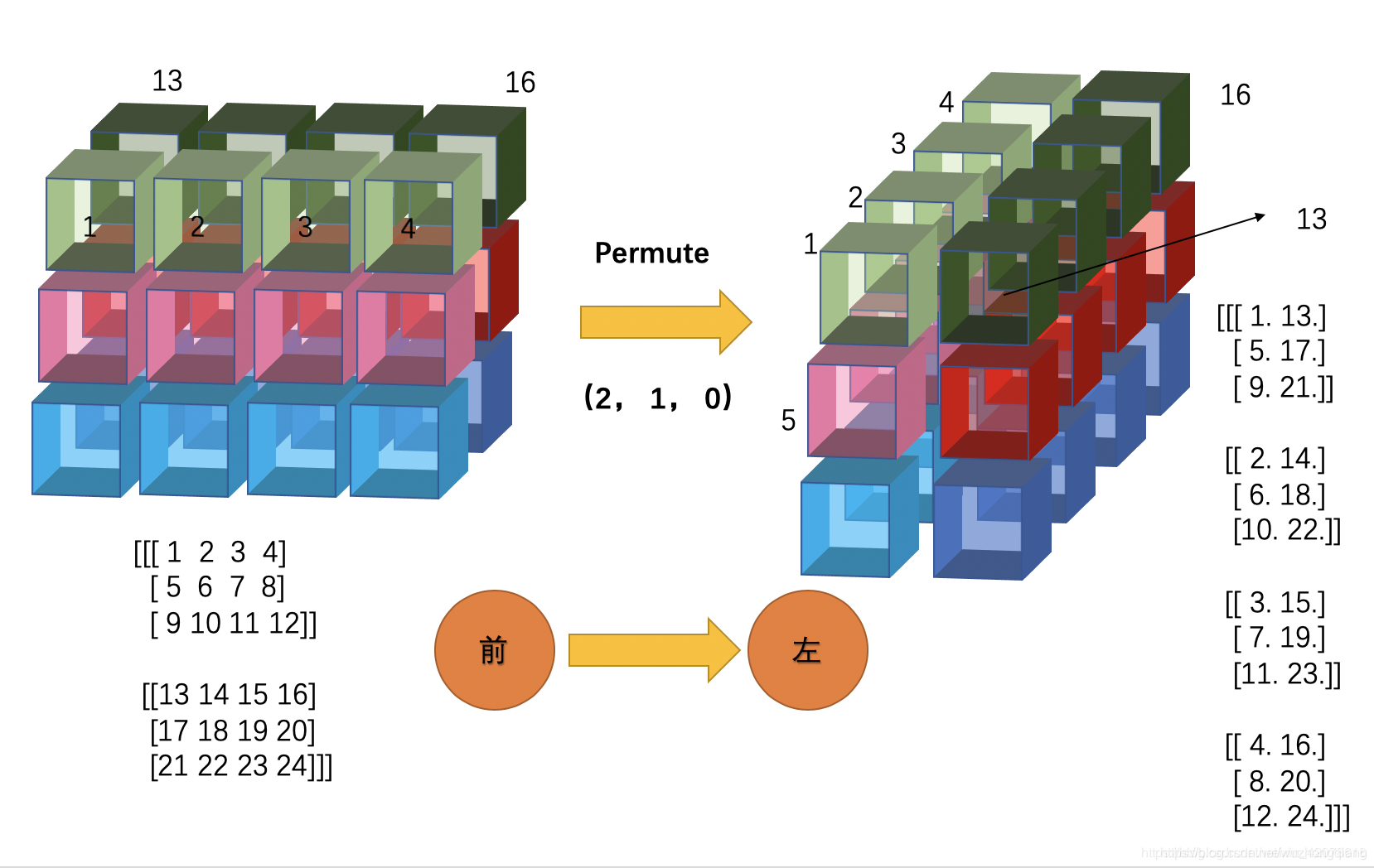
跑到右边，然后沿着axis=0逆序一下看，就得到最终结果。

只要明白了这个原理，其他的情况也都一样了， 其他的情况可以看
三维视图详解keras.permute_dimensions和numpy.transpose转置效果

哈哈，其实还是挺好玩的， 明白了这个视角的角度，也可以试一下axis=0,1，2的三维矩阵加法如何理解Axis？

最后说明一点， 其实这里为了看一下空间矩阵维度的变化细节才记录这个技巧的，其实在在真正的编程上，我们遇到的矩阵行数列数通道数等很多，我们根本没法去具体想象究竟是怎么去算的，并且一般我们实际的矩阵每个方向都有含义，比如[batchsize, time_step, seq_len]这种，转换的时候，我们只要理解是哪个维度的含义和哪个维度转就可以了，一般后两个转[batchsize, seq_len, time_step]这样，这样就基本上能看明白矩阵乘法以及矩阵乘法的含义了。 所以实际情况下不用理解那么细致。

最后就是要注意，上面那种技巧只是换了个角度去看矩阵，如果原来方向上都有特殊含义，可千万不要把特征含义给换了，只换axis帮助你纠正角度就可以。