WDK李宏毅学习笔记第九周01_Unsupervised Learning

本文主要是介绍WDK李宏毅学习笔记第九周01_Unsupervised Learning—linear model，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Unsupervised Learning—Linear Model

文章目录

Unsupervised Learning—Linear Model
摘要
引言
一、Dimension Reduction
- 1.1 化繁为简
- 1.2 Generation（无中生有）
二、Clustering（聚类）
- 2.1 Clustering是什么？
- 2.2 K-means
- 2.3 HAC (层次聚类)
三、Distributed Representation（分布式表达）
- 3.1 做dimension reduction的目标
- 3.2 Feature selection（特征选择）
- 3.3 Principle component analysis(PCA)
- 3.4 PCA - Another Point of View
- 3.5 Weakness of PCA
4、应用
- 4.1 Pokemon
- 4.2 MNIST
- 4.3、Matrix Factorization
结论

摘要

本章介绍了Dimension Reduction两种方法(“化繁为简”,“无中生有”)的基本思想，阐述了Clustering的基本思想及常用方法(K-means,HAC)的基本原理，重点说明了PCA的基本原理及其常见的应用(MNIST,Matrix Factorization等)。

引言

“化繁为简”是将多个图像的共性点抽象出来，“无中生有”是将多个图像作为label，然后寻找一组基础图片使得所有的label都可由基础图片线性组合得到。
Clustering的目的就是将输入进行分类，K-means的主要原理是用每一类的均值去更新center的vector，HAC的主要原理是建立树状图计算相似度进行分类。
只进行简单的分类会丢掉很多输入的信息，于是我们需要用Distributed Representation，用多个属性去描述输入，常用方法有feature selection和PCA，feature selection的思想是删除不重要的维度，PCA的思想是将输入作为model的label。然后找出一组basic component，这组basic component线性组合可以表示全部的label。

注：输入不用必须是图像，可以是能用vector表示的任何事物。

一、Dimension Reduction

Dimension Reduction分为两种，一种是“化繁为简”，一种是“Generation（无中生有）”。

1.1 化繁为简

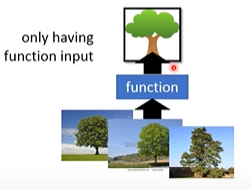
化繁为简是输入一个复杂的input，经过function处理后输出一个简单的output，该output能很好的表示input。例如：输入一些实际的树，这些树对应的输出都是相同的抽象的树。(如下图)
在这里插入图片描述

1.2 Generation（无中生有）

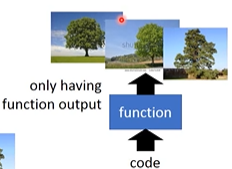
Generation要做的是训练一个function给现有的事物贴标签。例如：训练一个function，向该function输入一个code，然后就会输出对应的某一棵树，即使输入一个随机的code，机器也可以画出来一张图片，不同的输入，输出不同。
在这里插入图片描述

二、Clustering（聚类）

2.1 Clustering是什么？

Clustering就是用很多images训练一个function，向训练好的function输入image，就会输出该image的类别。也就是将image分类。

2.2 K-means

在Clustering最常用的方法就是K-means。K-means是怎样的？例如：我们有很多unlabeled data X1~XN(每个x都代表一张image)，要把它们做出k个cluster，这时就可用k-means，解决问题的关键就是我们需要找到每一个cluster的center(C1 ~ CK)，如何找？

我们可以用training data随机找K个image的vector来初始化center。
用center将training data进行分类。
分别将每一类的object取平均值，用该均值更新center，再重新从第2步开始，多次循环，得到最终的center。

2.3 HAC (层次聚类)

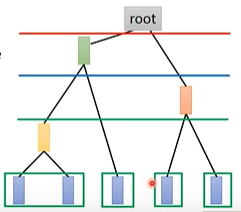
计算input两两之间相似度，将相似度最高的合并，然后重新计算两两之间的相似度，最高的合并，以此类推。例如现在有5个example(如下图蓝1~蓝5)，接下来进行下述操作：

我们计算蓝1~蓝五两两之间的相似度，若蓝1和蓝2相似度最大，就将蓝1和蓝2 merge起来，得到新的vector黄1，再计算黄1和蓝3 ~ 蓝5两两之间的相似度，若蓝4和蓝5相似度最大，就将其merge起来得到红1，再计算相似度，以此类推，得到如下的树形结构。
接下来我们可以对tree structure切一刀，若在下图蓝色线切一刀，就将5个example分为3类。若在红色处切一刀，就将其分为两组。

三、Distributed Representation（分布式表达）

在处理实际问题时，光做cluster是非常不够的，例如，做完cluster后，一张图片的label是树，但是我们不知道树的大小品种等等信息，这张图片的很多信息都被丢失了，所以我们需要用Distributed Representation，用多个属性去描述图片。Distributed Representation和Dimension Reduction做的事情是一样的，只是称呼不同。

3.1 做dimension reduction的目标

我们需要做的就是找一个function，这个function input一个高维的vector，output是一个低维的vector。
在这里插入图片描述
做dimension reduction常用的方法是Feature selection和Principle component analysis(PCA)。

3.2 Feature selection（特征选择）

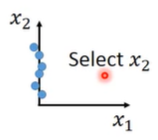
做dimension reduction里面最简单的是feature selection，例如：input是二维的，它的散点图如下图所示，我们可以发现它的分布与x1基本上无关，所有我们就删除该维度。但是这个方法并不是总有用的，当分布的维度是任何情况下都不可以拿掉的时候，我们就没法使用该办法了。
在这里插入图片描述

3.3 Principle component analysis(PCA)

PCA做的事情是，用很简单的linear function，input x和output z的关系就是x乘上一个矩阵W就得到output z，我们只需要根据一些input，将W找出来。

3.4 PCA - Another Point of View

另一个PCA比较直观的想法是，假设我们在做手写数字识别，这些数字其实就是由一些Basic Component(笔画)所组成的，如下图，数字"7"就可以用3个笔画表示。
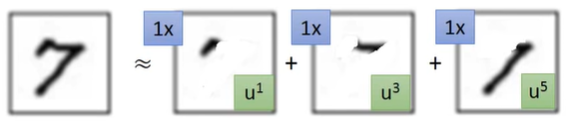
在这里插入图片描述
于是我们就可用如下的vector来表示"7"。

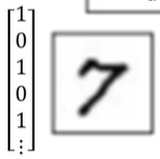
所以，数字就可用如下公式来表示：

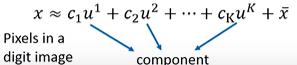
x表示手写数字的vector。
u表示所有笔画的vector。
c表示笔画前的系数(0或者1)。
$\frac{}{x}$ 表示所有x的vector的平均数。

于是我们可以得到：
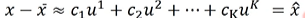
在这里插入图片描述
我们现在不知道u1~uk是什么，所以我们可以构造如下的loss function求u的值。

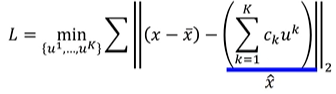
3.5 Weakness of PCA

PCA在处理样本data时，是将其投映到方差最大的地方，但是如果data是不同类的时候，投影后的数据将无法区别不同类的数据。
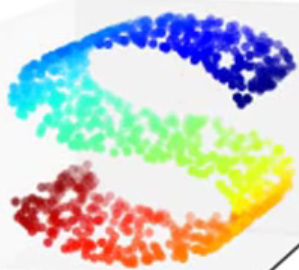
PCA是linear的，如果要将如下图片拉直，PCA是做不到的。

4、应用

4.1 Pokemon

有800只宝可梦，每只宝可梦都是用六个属性(HP，Atk，Def，Sp Atkins，Sp Def，Speed)表示，这样每个宝可梦都可以用一个6维的vector表示，我们可以用PCA按如下步骤对其分析：

对其进行分析处理，例如对六个宝可梦分析对其影响大的属性，一个常见的办法就是对每个属性算其对所有宝可梦算该属性值和的比率，

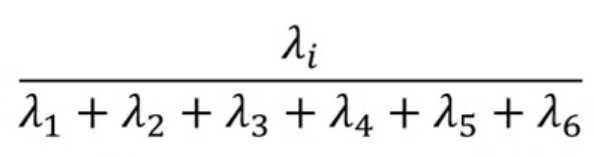
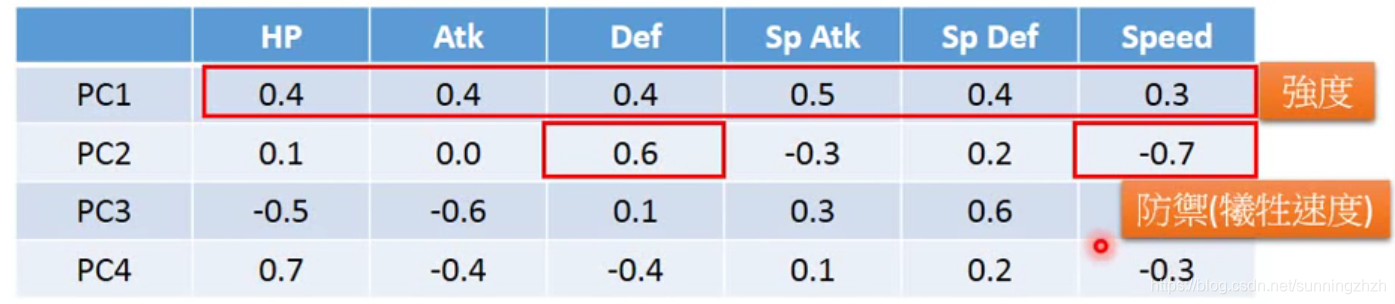
得到的结果如下，取4个影响(值)比较大的，我们认为这4个维度就可以区分不同的宝可梦。
我们再将不同的样本从这4个方向上进行投影，如此可以分析这4个方向分别代表什么及其含义。

4.2 MNIST

我们可以将每一张数字图片用多个图片的vector表示出来，其中每一个w都是一张image。
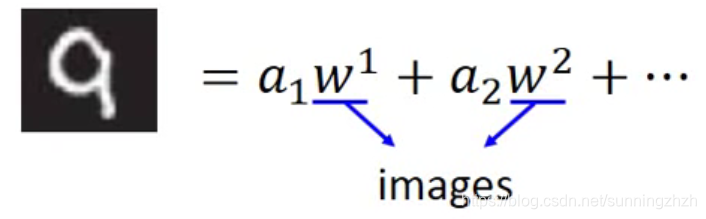
在这里插入图片描述
我们做PCA得到前30个component:

我们可以用这30个component表示手写数字0-9的图像。

4.3、Matrix Factorization

现在我们有5个人(A,B,C,D,E)拥有各个公仔的数目(如下图)，我们希望可以知道各个公仔和购买的人之间的联系。
在这里插入图片描述
我们用傲娇和呆萌这两个维度来表示人的性格和公仔的属性，首先做假设分析，如果公仔的属性和人的性格很接近，那么这个人就会购买更多的该公仔。但是人的性格和公仔属性是没法直接知道的。

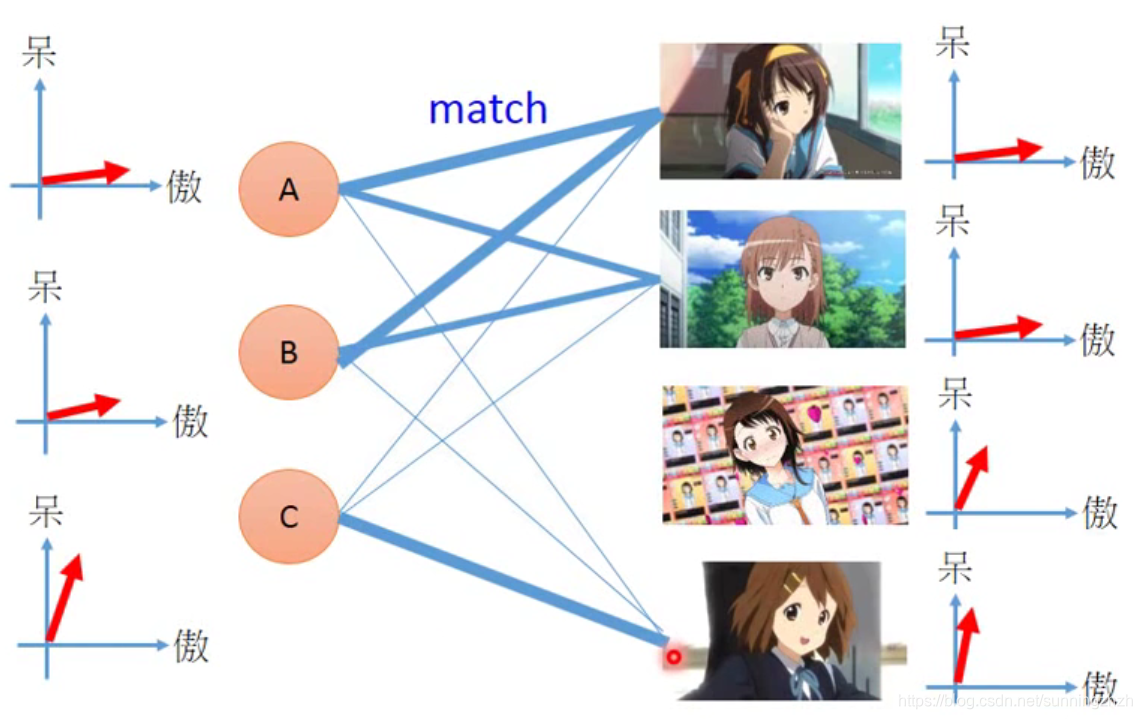
我们可以定义r(A,B,C,D,E)表示人物性格的vector，用r(1,2,3,4,5)表示公仔属性的vector，每个人购买某个公仔的数量就可用它们之间的内积表示，如此就可得到矩阵M=r(A,B,C,D,E) x r(1,2,3,4,5)T，我们就可以SVD求解了。
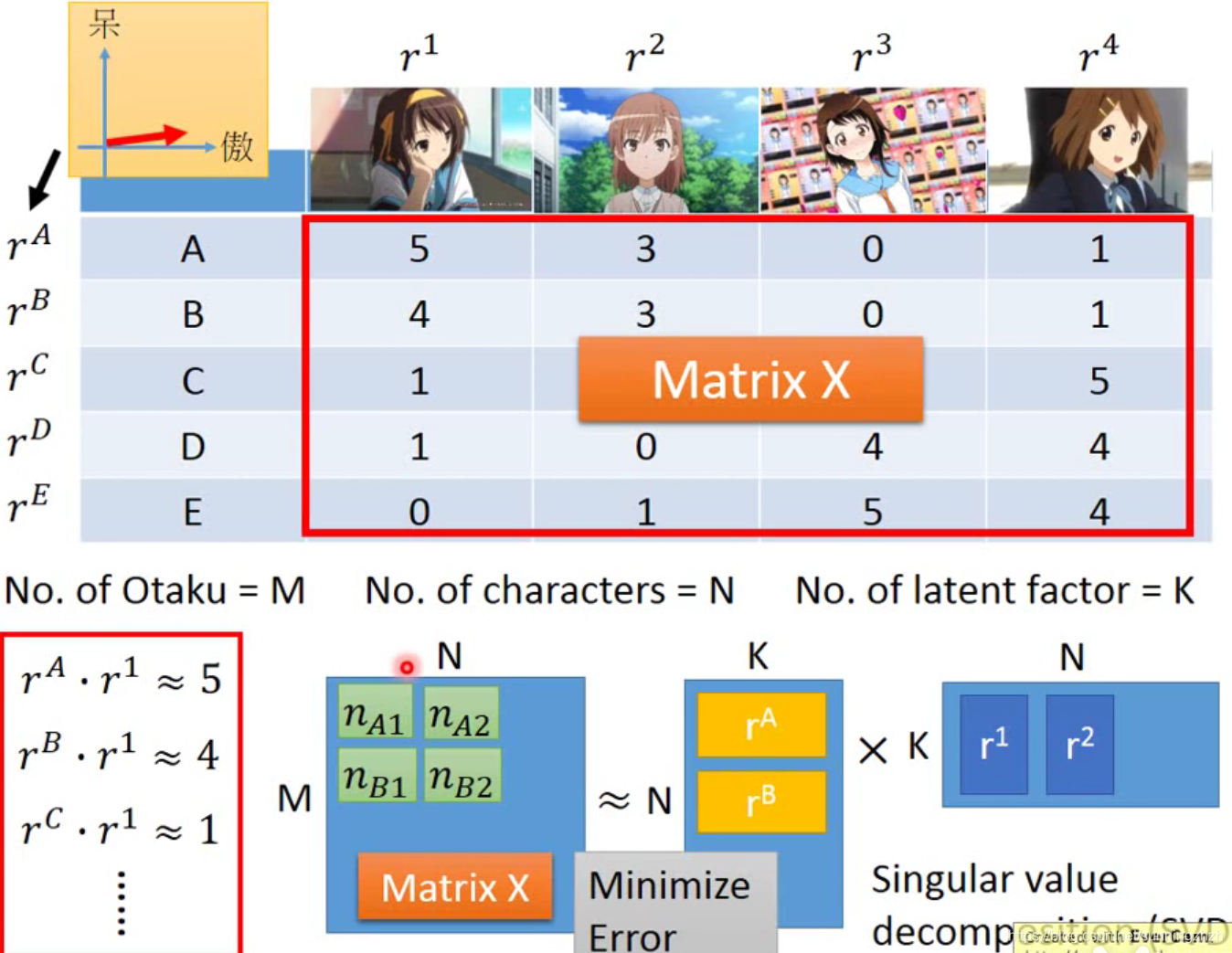
在这里插入图片描述
假如有些位置是空的，SVD求解就会不太好，这时我们可以构造一个loss function L，然后用梯度下降的方法来求解。

结论

对事物用cluster进行简单的分类时会丢失事物之间的很多信息，于是我们考虑用多个属性来描述某一类事物，最大程度上保存事物及该事物与其他事物之间关系的信息，常用的方法有feature selection和PCA，feature selection在实际使用中，无法处理feature的维度任何情况下都不可以拿掉的情况，PCA泛化性就强多了，它是找出事物的基本组成部分，用这些基本组成部分来描述事物，但是PCA得到的基本组成部分和我们人们想象的结果不太一样，可能会得到我们无法理解的component，这样不利于我们深入理解我们的model，可以用NMF解决该问题。

这篇关于WDK李宏毅学习笔记第九周01_Unsupervised Learning—linear model的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！