本文主要是介绍leading dimension,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
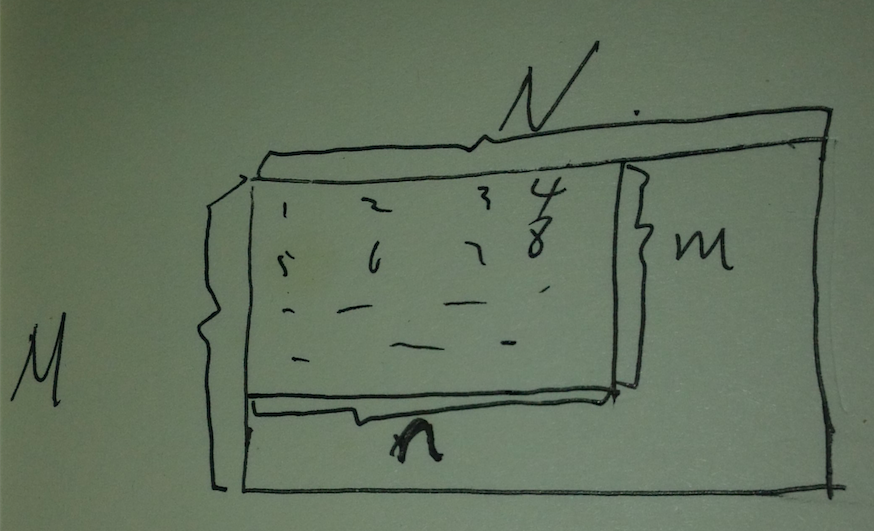
矩阵空间是 3x4,其左上角有一个子矩阵2x3,表示如下
11 22 33 0
44 55 66 0
0 0 0 0
i, j分别表示行索引,列索引
如果用列存储的话,leading dimension = 3(矩阵空间的行个数), 换算公式是i + j *ld
11 44 0 22 55 0 33 66 0 0 0 0
如果是用行存储, leading dimension = 4(矩阵空间的列个数),换算公式是 i*ld + j
11 22 33 0 44 55 66 0 0 0 0 0
cublas中矩阵用列存储表示,cusparse中的矩阵用行CNC表示
在cuda中二维数组是按照列存储的,在c中二维数组按照行存储,在c语言中的一个矩阵(二维数组)A = M X K, B = N X K, C = A * Bt = M x N
对于cuda而言(列存储),看到的A矩阵是K x M, B 是 K x N, 计算的C = Bt * A = N x M
计算结果C矩阵在c语言看来就是按照行存储的 M x N
在cuda中,对于A矩阵,不论在cublasSgemm, 是trans还是non-trans,其leading dimension就是 K, 同理对于矩阵B,是转置还是不转置,leading dimension都是K
在cuda中
设 A' = B = K x N , B' = A = K x M
transa = CUBLAS_OP_T
transb = CUBLAS_OP_N
m = op(A')_row = N
n = op(B')_col = M
k = op(A')_col = op(B')_row = K
lda = A'_row = K
ldb = B'_row = K
ldc = C_row = N
在c语言中有上图的矩阵,矩阵空间是 M x N, 但是只用到了mxn的子矩阵
对cuda而言,它看到的矩阵空间是NxM, 子矩阵是nxm
调用cublasSgemm,m,n,k都是用子矩阵的大小维度,但是lda = N
总结就是,gemm中的n,m,k都是计算的在cuda视角下子矩阵的维度,随着矩阵转置与否变化,但是lda是在cuda视角下矩阵空间的row的大小,并且不随矩阵转置与否变化
参考http://stackoverflow.com/questions/14595750/transpose-matrix-multiplication-in-cublas-howto
The problem is simple: I have two matrices, A and B, that are M by N, where M >> N. I want to first take the transpose of A, and then multiply that by B (A^T * B) to put that into C, which is N by N. I have everything set up for A and B, but how do I call cublasSgemm properly without it returning the wrong answer?
I understand that cuBlas has a cublasOperation_t enum for transposing things beforehand, but somehow I'm not quite using it correctly. My matrices A and B are in row-major order, i.e. [ row1 ][ row2 ][ row3 ]..... in device memory. That means for A to be interpreted as A-transposed, BLAS needs to know my A is in column-major order. My current code looks like below:
float *A, *B, *C;
// initialize A, B, C as device arrays, fill them with values
// initialize m = num_row_A, n = num_row_B, and k = num_col_A;
// set lda = m, ldb = k, ldc = m;
// alpha = 1, beta = 0;
// set up cuBlas handle ...这篇关于leading dimension的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!