leading专题
uva 11029 - Leading and Trailing(快速幂)
题目链接:uva 11029 - Leading and Trailing 题目大意:给出一个n和k求n^k的前三位数和后三位数。 解题思路:后三为数可以用分治的方法(快速幂)去做,可是前三位数就比较麻烦了,看了别人的题解. n^k = 10 ^ (k * log10(n)),所以可以将多余的位数移到小数点后面然后舍弃掉,只保留前三位,pow(10, 2 + fmod(k * l
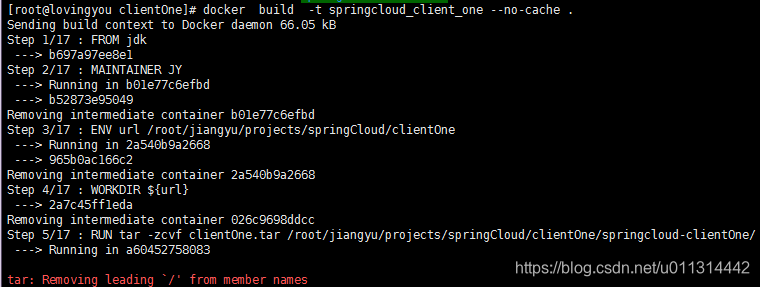
解决: tar: Removing leading `/‘ from member names
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到教程。 1. 我的情况 。 使用绝对路径 执行 tar 命令: tar -zcvf clientOne.tar /root/jiangyu/projects/springCloud/clientOne/springcloud-clientOne/ 报错如题: 2. 解决。 修改 t
大规模敏捷SA(Leading SAFe)证书是什么意思?如何报名,含金量高吗?
大规模敏捷SA(Leading SAFe)证书是什么意思? 常规的敏捷框架适用于中小型项目团队,而且不具有扩展性。基于常规的敏捷框架,SAFe定义了一个可扩展的敏捷框架模型,它适用于大型团队的合作开发,可以提高团队之间的协作性,降低团队管理的复杂性。 SAFe是目前国际上最流行的规模化敏捷方法,将敏捷实践从团队级(team level)有效扩展到项目群级(program level)乃至企业级
LightOJ 1282 Leading and Trailing
题意:求n^k的前三位和后三位。(n,k为大数) 分析: 后三位可以用快速幂得到(不足三位要补领0)。重点是求前三位。 n可以写成10^a(a为小数)的形式。因此 n^k = 10^(ak). 而ak可以写成x+y,其中x为ak的整数部分,y为ak的小数部分.其中x决定了位数,y决定了值。 因此只需求出y。 而n=10^a ,所以 a=log10(n) 这里用到了fmod函数,fmod(
Leading Robots 单调栈+排序
链接:http://acm.hdu.edu.cn/showproblem.php?pid=6759. 来源:杭电多校第一场 题目描述 给n个机器人的初始位置p和加速度a,在无限长的跑道中,有多少机器人能成为领头羊。 分析 我们可以把所有机器人按照起始位置递减的顺序进行排序,然后建立一个栈。 我们尝试去扫描所有的机器人,如果他的加速度比上一个机器人大,那么他一定可以超过他成为领头羊,那么把它
时序分析基本概念介绍Leading, Trailing edge
今天我们要介绍的时序分析概念是Leading, Trailing edge。 中文含义为主导,拖尾的边沿。 leading edge:主导的边沿,在每个周期中,第一个出现的边沿就是leading edge trailing edge:拖尾的边沿,在每个周期中,最后一个出现的边沿就是trailing edge leading edge不一定代表上升沿。反之,trailing edge也不一定
[iOS]Your package contains a file 'XXX.app/ XXX' with a name that contains leading or
今天提交一个APP到苹果,报错: ]Your package contains a file 'XXX.app/ XXX' with a name that contains leading or trailing whitespace characters 折腾了几个小时,最终发现问题:编译设置里面的product name 值多个了空格!
leading dimension
矩阵空间是 3x4,其左上角有一个子矩阵2x3,表示如下 11 22 33 0 44 55 66 0 0 0 0 0 i, j分别表示行索引,列索引 如果用列存储的话,leading dimension = 3(矩阵空间的行个数), 换算公式是i + j *ld 11 44 0 22 55 0 33 66 0 0 0 0 如果是用行存储, leadin
uva11029 - Leading and Trailing(头和尾)
求前缀和后缀(分别三位) 后缀容易求,只是取模求幂。。。。每次乘方后都取最后三位, 至于前缀,以前做过类似的题目,,,对于n^k来说,肯定可以用科学计数法来表示,由于太大我们无法存储,而我们也不需要知道它有多大,我们只是要3位, 所以,,,只需要求出小数部分,,指数部分用log求出来,去除整数部分,求10的pow(),,得到的即科学计数法的小数部分, 表达式:P = k*log10(n)




![[iOS]Your package contains a file 'XXX.app/ XXX' with a name that contains leading or](https://img-blog.csdn.net/20160125220143544?watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQv/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center)