图神经网络简介---A gentle introduction to Graph Neural Networks

1 什么是图

1.1 图的简单概念

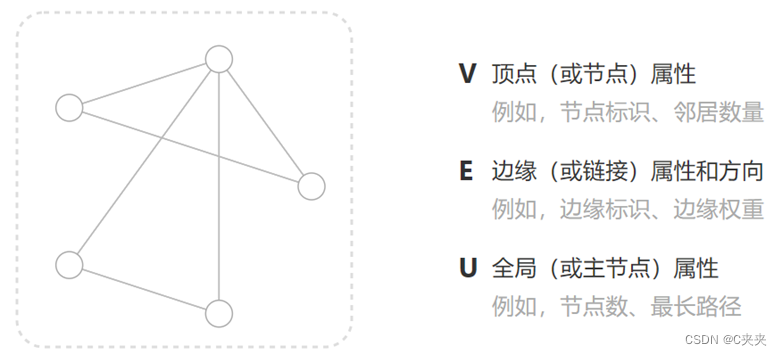
图是表示一些实体(nodes点)之间的关系(edges边)，可以在图的每个部分中存储信息。

通过将方向性与边（有向、无向）相关联来专门化图。分为无向图、有向图。

1.2 图的适用领域

对于图像和文本不太适用图表示，但举例将其作为图，有助于理解其它不太像网格的图形数据。

1. 以图形形式显示的图形

• 将图像视为具有图像通道的矩形网格，将其表示为数组(2442443)
• 将图像视为具有规则结构的图，每个像素代表一个节点，通过边缘连接到相邻像素。每个非边界像素正好8个相邻像素，存储在每个节点上的信息是表示像素RGB值的3维向量。
  
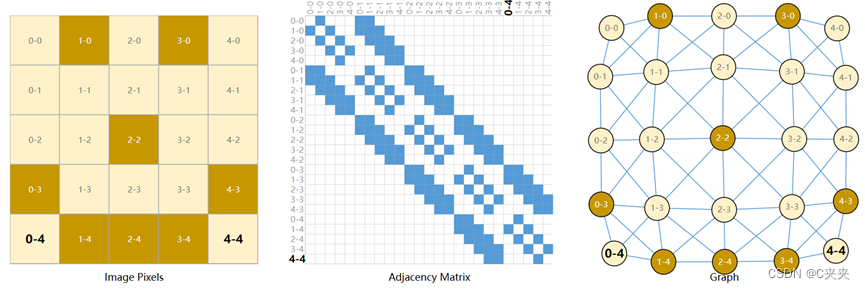
  可视化图形连通性的一种方法：邻接矩阵。以上三种表示形式都是同一数据的不同视图。

2. 以图形形式显示的文本
   通过将索引与每个字符、单词或标记相关联，并将文本表示为这些索引的序列来数字化文本。这将创建一个简单的有向图，其中每个字符或者索引都是一个节点，通过边连接到后面的节点。
   
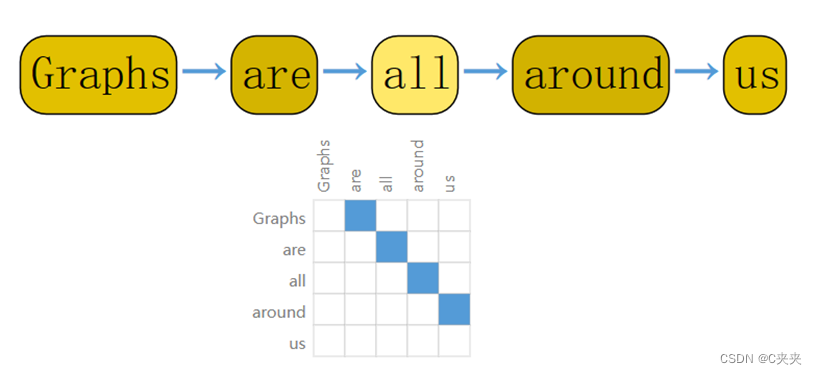
   在实践中，一般不用图作为文本和图像的编码方式，因为所有图像和文本都具有非常规则的结构，用图表示显得多余。
   例如：图像在其邻接矩阵中具有带状结构，因为所有节点（像素）都连接在一个网格中。文本的邻接矩阵是一条对角线，因为每个单词只连接到前一个单词和下一个单词。

3. 分子、社交网络、引文网络通常用图表示
   这些示例，每个节点的领域数是可变的，除了图很难用其它方式表示。

4. 计算机视觉
   在视觉场景中标记对象，可以将对象视为节点，将它们关系视为边来构建图。

5. 机器学习模型、编程代码、数学方程式
   变量作为节点，变量作为输入和输出的操作视为边。某些文献中使用术语“数据流图”。

1.3 图结构化数据存在的问题

1.3.1 图级任务

预测整个图的单个属性。即给出一张图，对这张图进行分类—将标签与整个图像相关联。
例如：

• 表示为图的分子，想要预测该分子闻起来是什么味道，或者它是否会与与疾病有关的受体结合。
• 对于文本作情感分析，希望一次识别整个句子的情绪或情感。

1.3.2 节点级任务

预测图中某些节点的属性。即涉及预测图中每个节点的身份/角色。

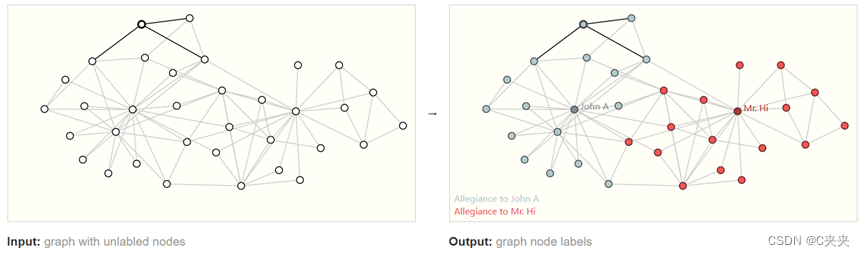
左边是问题的初始条件，右边是可能的解决方案，其中每个节点都根据联盟进行了分类。
例如：

• 按照图像类比，节点级预测问题类似于图像分割，试图标记图像中每个像素的角色。
• 对于文本，类似的任务是预测句子中每个单词（例如名词、动词、副词等）的词性。

1.3.3 边缘级任务

预测图中边缘的属性或存在。即给出图，需要预测出每条边上的属性—预测关系。
例子：

• 图像场景理解。除了识别图像中的对象外，深度学习模型还可用于预测它们之间的关系。我们可以将其表述为边缘级分类：给定表示图像中对象的节点，我们希望预测这些节点中哪些共享一条边或该边的值是多少。如果我们希望发现实体之间的联系，我们可以认为图是完全连接的，并根据它们的预测值修剪边缘以得出稀疏图。
  
  

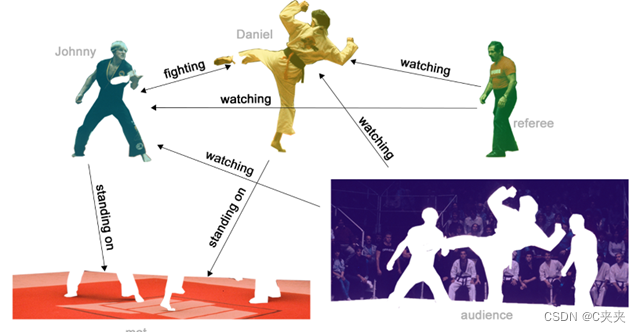
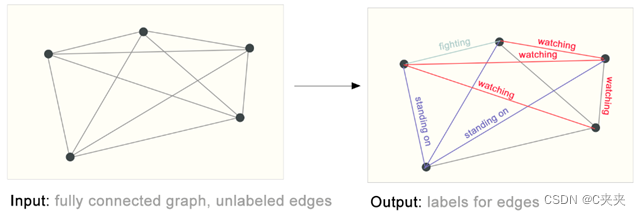
1.4 在机器学习中使用图形的挑战

机器学习模型通常采用矩形/网格状数组作为输入。
那如何表达图使得其与神经网络兼容？
节点、边缘、全局信息均可用向量表示，主要考察连通性的表示。

• 邻接矩阵：其容易张量，但是这种表示方式有一些缺点。例如图中的节点数可能达到数百万个，并且每个节点的边数可以高度可变。通常，这会导致非常稀疏的邻接矩阵，这些矩阵的空间效率低下。另一个问题是，有许多邻接矩阵可以编码相同的连通性，并且不能保证这些不同的矩阵会在深度神经网络中产生相同的结果（也就是说，它们不是排列不变的）。例如有些可以用两个不同的邻接矩阵等效地描述，它也可以用节点的所有其他可能的排列来描述。
• 邻接列表：描述了边缘的连通性。由于我们期望边数远低于邻接矩阵的条目数，避免在图的不连接部分进行计算和存储。为了使这个概念具体化，我们可以看到不同图中的信息在这个规范下是如何表示的。
  
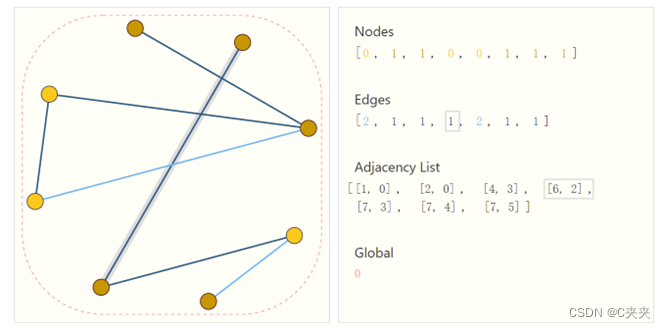
  Adjacency list：邻接列表，长度是边的长度。它的第i项表示的是第i个边，存储所有边和属性。

2 基于消息传递的图神经网络

GNN是对图的所有属性(节点、边、全局上下文)的可优化转换，保留了图的对称性（排列不变性）。
GNN 采用“图输入，图输出”架构，图作为输入，将信息加载到其节点、边缘和全局中，并逐步转换这些嵌入， 而不更改输入图的连通性。
使用Gilmer 等人提出的“信息传递神经网络”框架构建 GNN，并使用 Battaglia 等人介绍的图网络架构原理图。

2.1 最简单的GNN—学习图属性的新嵌入，不使用图的连通性

• 在图的每个组成部分上使用一个单独的多层感知器（MLP），称之为GNN层。
• 对于每个节点向量，应用 MLP 并返回一个学习到的节点向量。对每条边学习每条边的嵌入，对全局上下文向量学习整个图的单个嵌入。
  
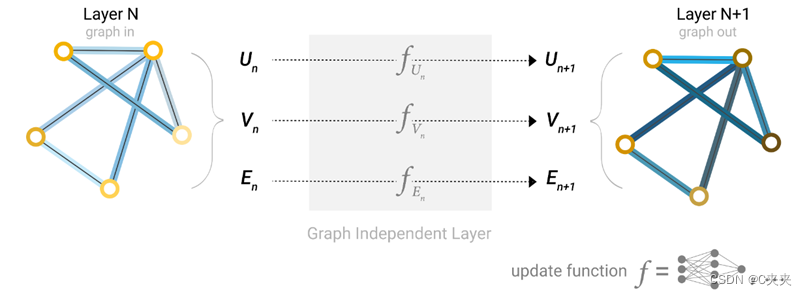
• 简单 GNN 的单层：图形是输入，每个组件 （V，E，U） 由 MLP 更新以生成新图形。
• 图输入—图更新输出（对属性变换，但不改变图的结构）
• 每个函数下标表示 GNN 模型第 n 层上不同图形属性的单独函数。
• 与神经网络模块或层一样，可以将这些GNN层堆叠在一起。由于 GNN 不会更新输入图的连通性，因此可以描述具有与输入图相同的邻接列表和相同数量的特征向量的 GNN 的输出图。但是，输出图更新了嵌入，因为 GNN 更新了每个节点、边缘和全局上下文表示。

2.2 通过池化信息预测的 GNN

如何在上面描述的任务中做出预测？

• 考虑二元分类，但这个框架很容易扩展到多类/回归的情况。
• 若任务是在节点上进行二元预测，并且图上已包含节点信息，则方法很简单—对于每个节点嵌入，应用线性分类器。
• 所有顶点共享一个全连接层。
  
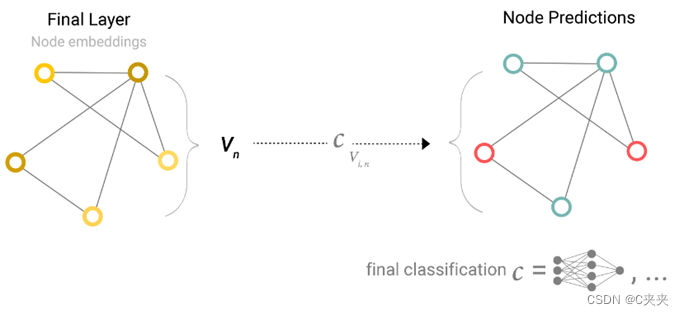
  然而，事情不会这么简单。例如：能将图形中的信息存储在边中，但在节点中没有信息，但仍需要对节点进行预测。需要一种方法来从边缘收集信息并将其提供给节点进行预测。
  通过池化来完成这个要求：即对点做预测，但是点没有向量，则将该点周围与其连接的边向量加起来得到该点的向量。
  
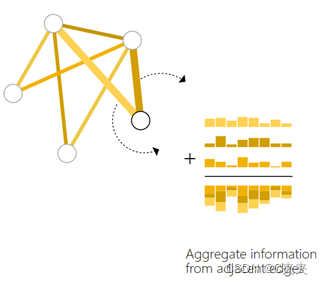
  池化的步骤：

1. 对于要池化的每个项目，收集它们的每个嵌入并将它们连接成一个矩阵。
2. 通常通过求和运算聚合收集的嵌入。
3. 用字母ρ表示池化，正在收集从边到节点的信息：ρEn—>Vn
   
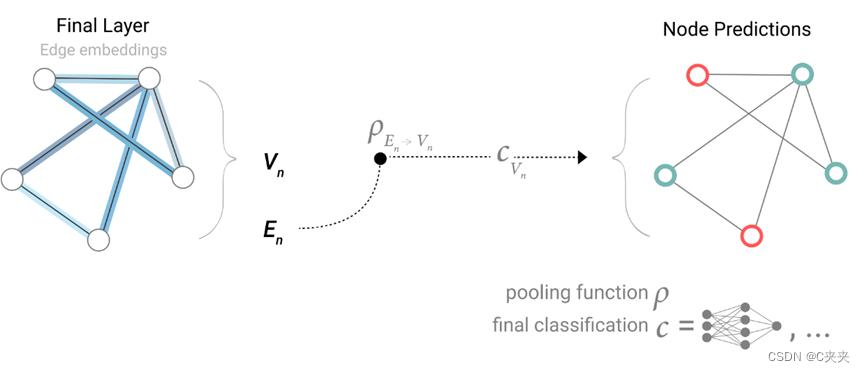
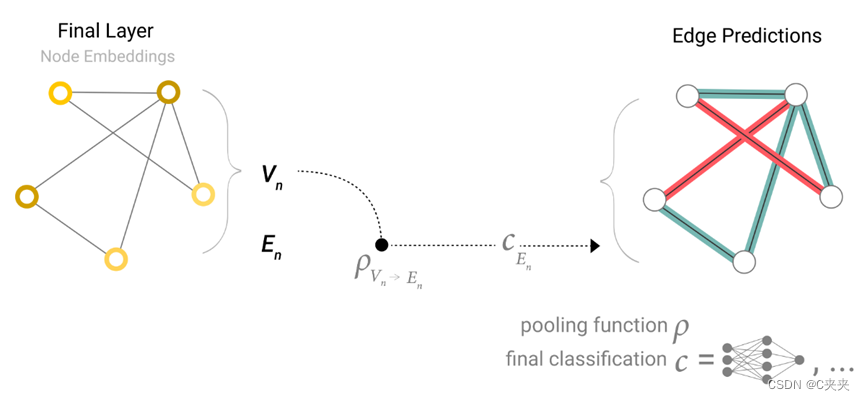
   如果只有节点级特征，并试图预测二进制边缘级信息，则模型如下所示。同理：将顶点的向量汇聚到边上。
   
   如果只有节点级特征，需要预测二进制全局属性，则需要将所有可用的节点信息收集在一起并聚合它们。这类似于 CNN 中的 Global Average Pooling 图层。对边缘也可以这样做,将所有顶点向量加起来输入到全局层得到全局的向量。
   
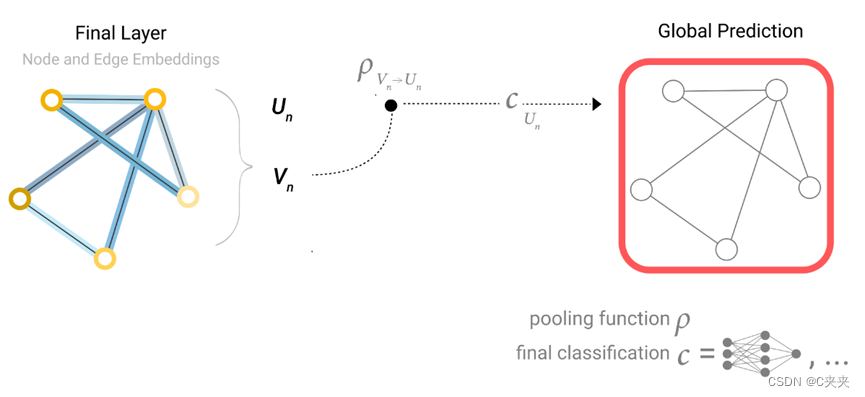
   示例中，分类模型c可以很容易地用任何可微分模型替换，或者使用广义线性模型适应多类分类。
   
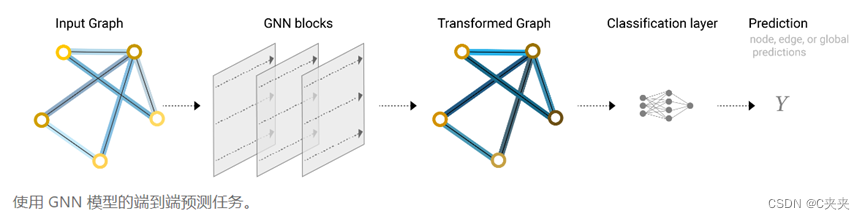
   流程：
   输入图—>进入一系列GNN层—>输出保持图结构，但所有属性均改变—>输出信息添加合适输出层，缺失信息添加合适汇聚层—>完成预测
   这个简单图神经网络的局限性：

• 在GNN层，未添加图属性，并未合理的将整个图的信息更新至图里面，导致最后结果不是很好。
• 如果有新的图形属性，只需要定义如何将信息从一个属性传递到另一个属性。
• 在这个最简单的 GNN 公式中，根本没有在 GNN 层内使用图的连通性。每个节点都是独立处理的，每个边以及全局上下文也是如此。仅在汇集信息进行预测时才使用连通性。

2.3 在图像的各部分之间进行信息传递

可以通过在GNN层中使用池化来做出更复杂的预测，以便学习的嵌入意识到图的连通性。可以使用消息传递来做到这一点，其中相邻节点或边缘交换信息并影响彼此更新的嵌入。
消息传递分三个步骤进行：

1. 对于图中每个节点，收集所有相邻的节点嵌入(或消息)
2. 通过聚合函数聚合所有消息(如sum)
3. 所有池化信息都通过更新函数(通常是学习的神经网络)传递
   
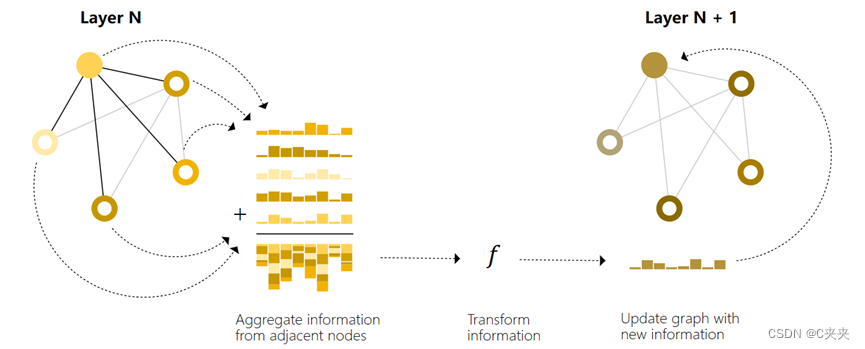
   任务：对顶点向量进行更新
   之前方法：将向量拿过来进入f(即MLP)，直接得到顶点向量的更新
   信息传递方法：将该顶点向量与其邻居向量都加在一起得到汇聚的向量，将汇聚的向量进入f进行后续操作，得到此顶点向量的更新

类似于标准卷积：从本质上讲，消息传递和卷积是聚合和处理元素邻居信息以更新元素值的操作。在图中，元素是一个节点，而在图像中，元素是一个像素。但是，图中相邻节点的数量可以是可变的，这与图像中每个像素都有一定数量的相邻元素不同。即若联想卷积，则每个加权和均一样。这样最后一层，会将整个图邻居的邻居等等全部汇合过来，从而完成整个图。

通过将传递GNN的消息层堆叠在一起，一个节点最终可以整合来自整个图的信息：在三层之后，一个节点拥有距离它三步远的节点的信息。
可以更新架构图，以包含节点的这个新信息源：

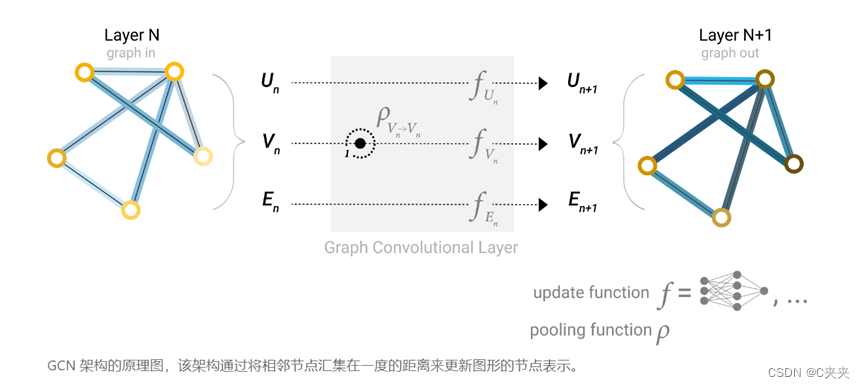
2.4 学习边缘表示

• 数据集并不总是包含所有类型的信息（节点、边缘和全局上下文）。
• 当想对节点进行预测，但数据集只有边缘信息时，在上面展示了如何使用池化将信息从边缘路由到节点，但仅限于模型的最后预测步骤
• 可以使用消息传递在 GNN 层内的节点和边之间共享信息。
• 可以像之前使用相邻节点信息一样，通过汇集边缘信息，使用更新函数对其进行转换，然后存储它，来合并来自相邻边缘的信息。
  然而，存储在图中的节点和边信息不一定具有相同的大小或形状，因此如何组合它们并不清楚。
• 方法一：学习从边空间到节点空间的线性映射，反之亦然。
• 方法二：可以在更新函数之前将它们连接在一起。
  即维度不一样则进行投影，顶点到边，边到顶点之后再到各自的MLP做更新
  
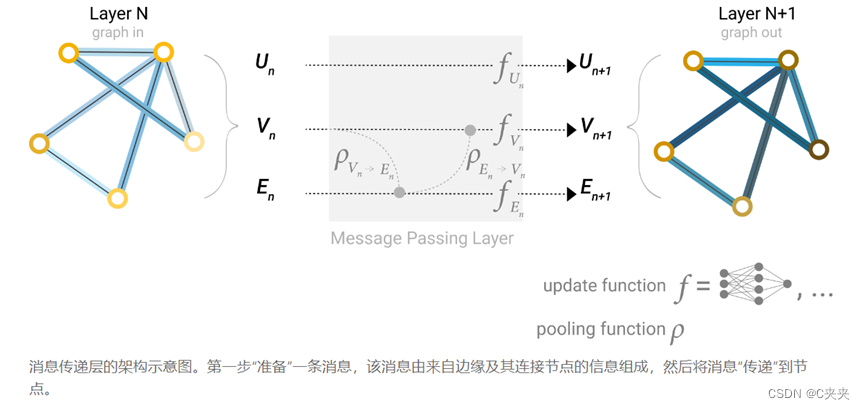
  在构建 GNN 时，更新哪些图形属性以及更新它们的顺序是一个设计决策。
• 可以选择是在边缘嵌入之前更新节点嵌入，还是相反。这是一个具有各种解决方案的开放研究领域——例如，可以以“编织”的方式进行更新，其中有四个更新的表示，这些表示被组合成新的节点和边缘表示：节点到节点（线性）、边缘到边缘（线性）、节点到边缘（边缘层）、边缘到节点（节点层）
• 或者交替更新，即同时顶点汇聚到边，边汇聚到顶点
  

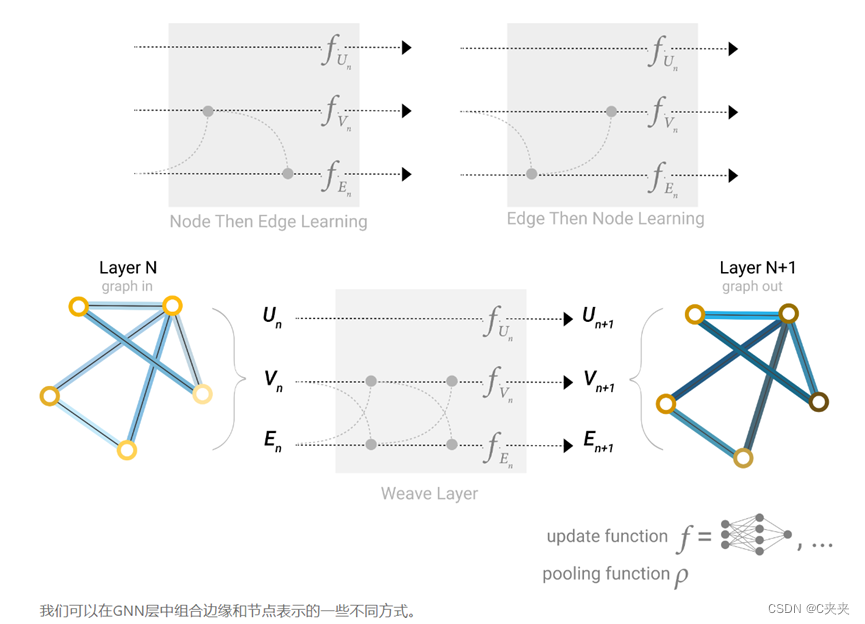
2.3 添加全局表示

以上所描述的网络均存在一个缺陷：即使多次应用消息传递，图中彼此相距较远的节点可能永远无法有效地相互传输信息。对于一个节点，如果有 k 层，信息最多会在 k 步外传播。如果预测任务依赖于相距很远的节点或节点组，这可能是一个问题。
解决方法：

1. 让所有节点能够相互传递信息。但对于大型图，会变得计算成本高昂（尽管这种方法被称为“虚拟边”，已被用于分子等小图）。
2. 使用图形 （U） 的全局表示，有时称为主节点master node或上下文向量context vector。这个全局上下文向量连接到网络中的所有其他节点和边缘，可以充当它们之间的桥梁来传递信息，从而为整个图形构建表示。这创建了比以其他方式学习的更复杂的图形表示。
   Master node：这个点是虚拟节点，可以与所有点和边相连U
   
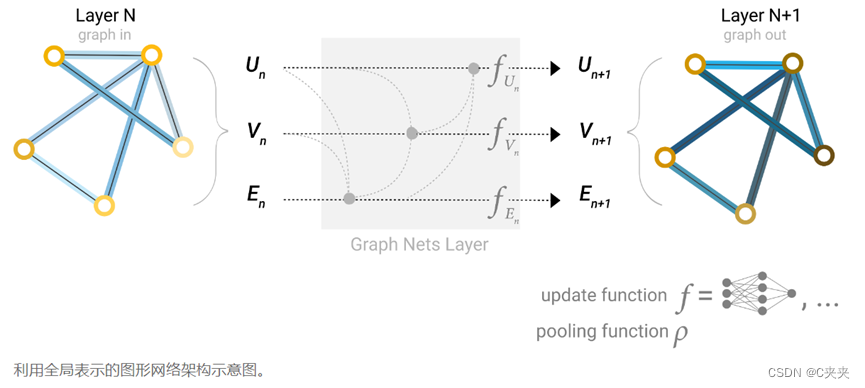
   所有图属性都学习了表示，因此可以在池化过程中通过调节感兴趣的属性相对于其余属性的信息来利用它们。
   例如，对于一个节点，可以考虑来自相邻节点、连接边和全局信息的信息。为了在所有这些可能的信息源上嵌入新节点，可以简单地将它们连接起来。此外，还可以通过线性映射将它们映射到同一空间，并将它们添加或应用特征调制层，这可以被认为是一种特征性注意力机制。
   
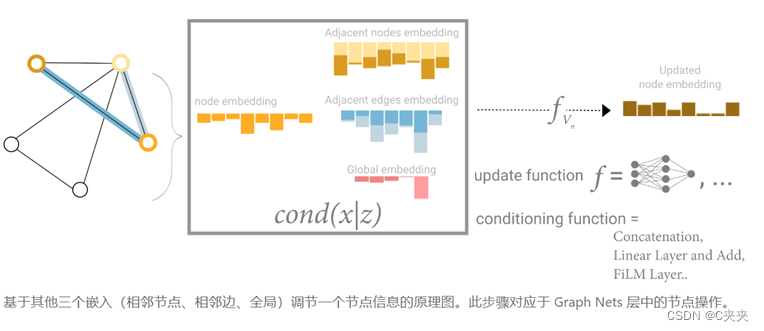
   将来自相邻的属性可以加在一起/合并在一起。

3 实验

3.1 GNN Playground

1. Playground 展示了一个带有小分子图的图级预测任务。

• 使用 Leffingwell 气味数据集，该数据集由具有相关气味感知（标签）的分子组成。预测分子结构（图形）与其气味的关系是一个有100年历史的问题，横跨化学、物理学、神经科学和机器学习。
• 为了简化问题，只考虑每个分子的单个二元标记，对分子图是否闻起来“刺鼻”进行分类。
• 将每个分子表示为一个图，其中原子是包含其原子身份（碳、氮、氧、氟）的一热编码的节点，键是包含一热编码其键类型（单键、双键、三键或芳香族）的边缘。
• 使用连续的 GNN 层构建针对此问题的通用建模模板，然后使用具有 S 形激活的线性模型进行分类。

2. 具体参数说明：

• 更新时每个属性的维度。更新函数是一个 1 层 MLP，具有 relu 激活函数和用于激活归一化的层范数。
• 池化中使用的聚合函数：最大值、平均值或总和。
• 更新的图形属性或消息传递的样式：节点、边和全局表示。通过布尔切换（打开或关闭）来控制它们。
• 基线模型是一个与图无关的 GNN（所有消息传递），将末尾的所有数据聚合到一个全局属性中。切换所有消息传递函数会产生 GraphNets 架构。

3. 更好地理解 GNN 如何学习图的任务优化表示—研究了 GNN 的倒数第二层激活。
   
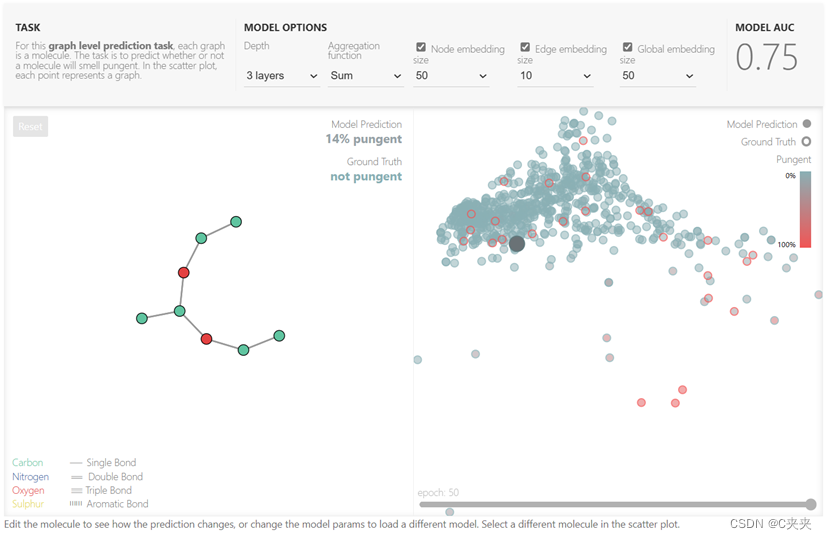
   可以选图神经网络有多少层，汇聚的操作：平均值、加起来、max，顶点、边、全局的向量有多大，每改变一次超参数，则会对其重新做一次训练。真实值用边框表示，预测值用实心表示。若边框和实心都是红色/蓝色，则预测正确。

3.2 一些GNN设计教训的经验

散点图中的每个点都表示一个模型：x 轴是可训练变量的数量，y 轴是性能。

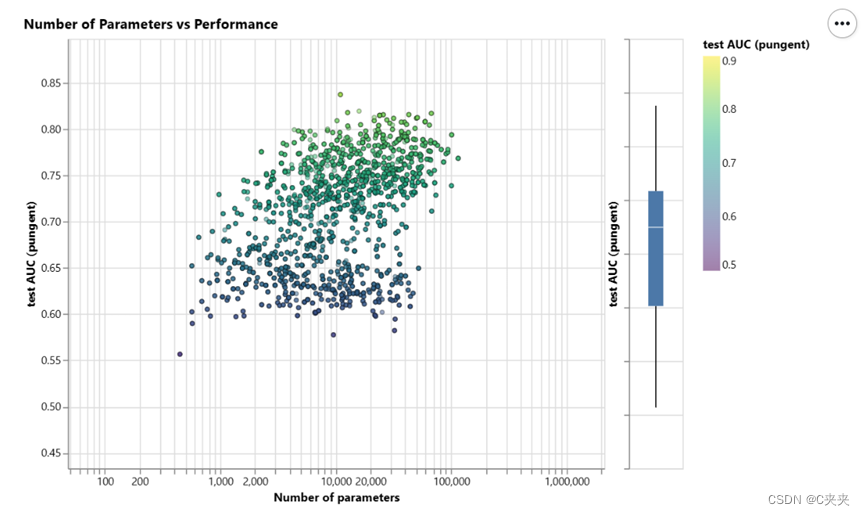
当模型数变高，整个AUC的上限是增高。即更多的参数确实与更高的性能相关。
GNN是一种参数效率非常高的模型类型：即使是少量的参数（3k），我们也已经可以找到高性能的模型。

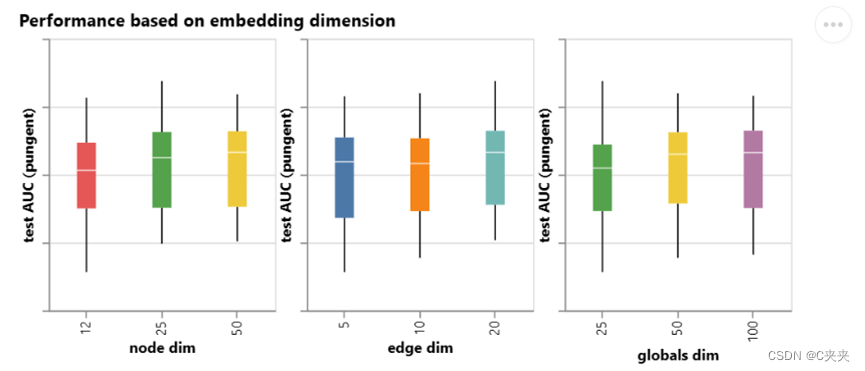
具有较高维数的模型往往具有更好的均值和下界性能，但在最大值下没有发现相同的趋势。可以找到一些性能最佳的型号，用于较小的尺寸。由于维数越高，参数数量越多，因此这些观测结果与上图相辅相成。

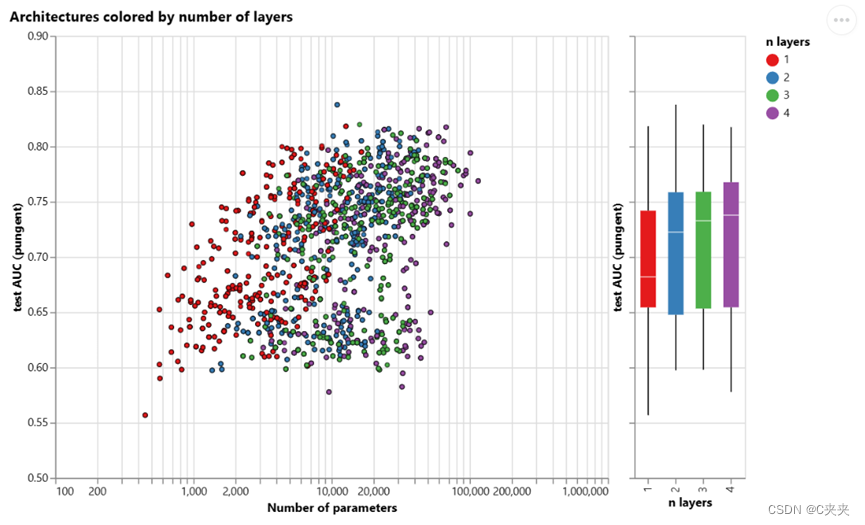
每个点都按层数着色。可以将层数调高些，但也必须将参数调好。
箱形图显示了类似的趋势，虽然平均性能倾向于随着层数的增加而增加，但性能最好的模型没有三层或四层，而是两层。此外，性能的下限随着四层的增加而降低。这种效应之前已经观察到，具有更多层数的GNN将在更高的距离上广播信息，并且可能会有其节点表示从许多连续迭代中“稀释”的风险。
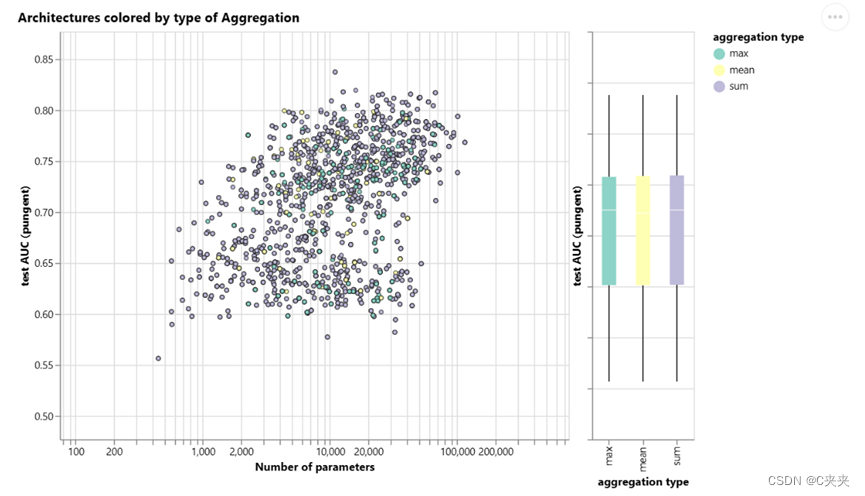每个点都按聚合类型着色。总和似乎对平均性能有非常轻微的改善，但最大值或均值可以给出同样好的模型。在查看聚合操作的判别/表达能力时，这对于上下文化很有用。
之前的探索给出了好坏参半的信息。我们可以找到平均趋势，其中更高的复杂性会带来更好的性能，但我们可以找到明确的反例，其中参数、层数或维度较少的模型表现更好。一个更明显的趋势是关于相互传递信息的属性数量。
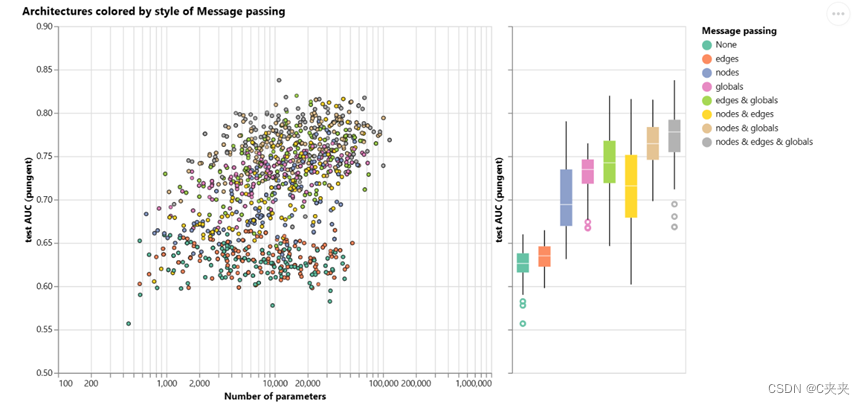绿色表示不传递任何信息，即一开始最简单的GNN图。

• 总的来说，图形属性的交流越多，平均模型的性能就越好。任务以全局表示为中心，因此显式学习此属性也往往会提高性能。节点表示似乎也比边表示更有用，这是有道理的，因为这些属性中加载了更多信息。
• 从这里可以有很多方向来获得更好的性能。希望两个突出两个大方向，一个与更复杂的图算法有关，另一个与图本身有关。
• 到目前为止， GNN 基于基于邻域的池化操作。有一些图形概念很难用这种方式表达，例如线性图形路径（连接的节点链）。设计可以在GNN中提取、执行和传播图信息的新机制是当前的一个研究领域。
• GNN研究的前沿之一不是制作新的模型和架构，而是“如何构建图”，更准确地说，是为图注入可以利用的额外结构或关系。正如粗略地看到的，传达的图形属性越多，就越倾向于拥有更好的模型。在这种特殊情况下，可以考虑通过在节点之间添加额外的空间关系、添加不是键的边缘或子图之间的显式可学习关系来使分子图的特征更加丰富。

4 相关技术

4.1 其它图类型(多图、超图、超节点、分层图)

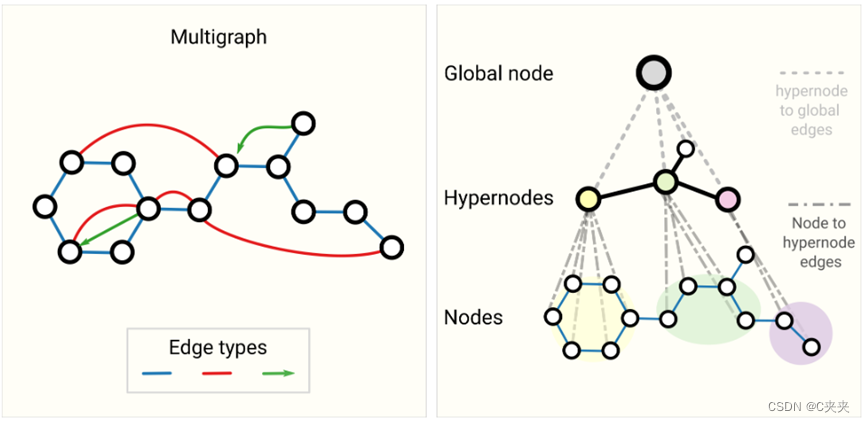
第一个：多个图，顶点之间可能会有多个边
第二个：图可能是分层的，最后一层由于消息传递可以看到一个很大的图
消息传递框架足够灵活，通常使GNN适应更复杂的图结构是关于定义信息如何通过新的图属性传递和更新。
例如，我们可以考虑多边图或多图，其中一对节点可以共享多种类型的边，当我们想根据节点的类型以不同的方式对节点之间的交互进行建模时，就会发生这种情况。例如，对于社交网络，我们可以根据关系类型（熟人、朋友、家人）指定边缘类型。GNN 可以通过为每种边缘类型设置不同类型的消息传递步骤来调整。 我们还可以考虑嵌套图，例如节点表示图，也称为超节点图。嵌套图可用于表示分层信息。例如，我们可以考虑一个分子网络，其中节点代表一个分子，如果我们有一种将一个分子转化为另一个分子的方法（反应），则两个分子之间共享一条边。 在这种情况下，我们可以通过让一个 GNN 在分子水平上学习表示，另一个在反应网络水平上学习表示，并在训练期间在它们之间交替学习，从而在嵌套图上学习。
另一种类型的图是超图，其中一条边可以连接到多个节点，而不仅仅是两个节点。对于给定的图，我们可以通过识别节点社区并分配连接到社区中所有节点的超边来构建超图。

4.2 GNN 中的采样图和批处理

训练神经网络的常见做法是使用根据训练数据的随机常量大小（批量大小）子集（小批量）计算的梯度来更新网络参数。这种做法给图形带来了挑战，因为彼此相邻的节点和边的数量是可变的，这意味着我们不能有一个恒定的批量大小。使用图形进行批处理的主要思想是创建子图，以保留较大图形的基本属性。此图形采样操作高度依赖于上下文，并且涉及从图形中子选择节点和边。这些操作在某些上下文（引文网络）中可能是有意义的，而在另一些上下文中，这些操作可能太强了（分子，其中子图仅表示一个新的、更小的分子）。如何对图进行采样是一个开放性研究问题。如果我们关心在邻域级别上保留结构，一种方法是随机抽样均匀数量的节点，即我们的节点集。然后添加与节点集相邻的距离为 k 的相邻节点，包括它们的边。每个邻域都可以被视为一个单独的图，GNN可以在这些子图的批次上进行训练。损失可以被掩盖为仅考虑节点集，因为所有相邻节点都具有不完整的邻域。 更有效的策略可能是首先随机抽取单个节点，将其邻域扩展到距离 k，然后在扩展集合中选取另一个节点。一旦构造了一定数量的节点、边或子图，这些操作就可以终止。 如果上下文允许，我们可以通过选择初始节点集，然后对恒定数量的节点进行子采样（例如随机，或通过随机游走或 Metropolis 算法）来构建恒定大小的邻域。

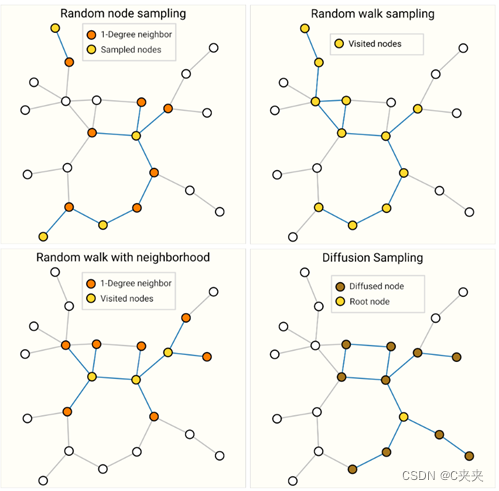
1. 随机采样一些点，将采样的邻居表示出来
2. 规定随机走多少步
3. 结合两种
4. 随机取一点，进行宽度遍历
   对同一图形进行采样的四种不同方法。抽样策略的选择很大程度上取决于上下文，因为它们将生成不同的图形统计分布（# 节点、#edges 等）。对于高度连接的图形，还可以对边进行二次采样。
   当图形足够大以至于无法放入内存中时，对图形进行采样尤为重要。启发新的架构和训练策略，例如 Cluster-GCN 和 GraphSaint。我们预计图形数据集的规模将在未来继续增长。

4.3 电感偏置

在构建模型以解决特定类型数据的问题时，我们希望将模型专业化以利用该数据的特征。当这成功完成时，我们通常会看到更好的预测性能、更短的训练时间、更少的参数和更好的泛化。
例如，在图像上标记时，我们希望利用这样一个事实，即无论狗是在图像的左上角还是右下角，它仍然是狗。因此，大多数图像模型使用卷积，卷积是平移不变的。对于文本，标记的顺序非常重要，因此递归神经网络按顺序处理数据。此外，一个标记（例如“not”一词）的存在会影响句子其余部分的含义，因此我们需要可以“参与”文本其他部分的组件，而 BERT 和 GPT-3 等转换器模型可以做到这一点。这些是归纳偏差的一些例子，我们正在识别数据中的对称性或规律性，并添加利用这些属性的建模组件。
对于图，我们关心每个图组件（边、节点、全局）如何相互关联，因此我们寻找具有关系归纳偏差的模型。模型应保留实体之间的显式关系（邻接矩阵）并保留图对称性（排列不变性）。不管怎么交换顶点顺序，GNN对他的作用都是保持不变的。我们预计实体之间的交互很重要的问题将受益于图结构。具体来说，这意味着在集合上设计变换：节点或边上的操作顺序应该无关紧要，并且操作应该在可变数量的输入上工作。

4.4 比较聚合操作

汇集来自相邻节点和边缘的信息是任何相当强大的GNN架构中的关键步骤。由于每个节点都有可变数量的邻居，并且由于我们想要一种可微分的方法来聚合此信息，因此我们希望使用平滑聚合操作，该操作与节点排序和提供的节点数不变。
选择和设计最佳聚合操作是一个开放的研究课题。聚合操作的一个理想属性是，相似的输入提供相似的聚合输出，反之亦然。一些非常简单的候选置换不变运算是求和、均值和最大值。方差等汇总统计量也有效。所有这些都采用可变数量的输入，并提供相同的输出，无论输入顺序如何。让我们来探讨一下这些操作之间的区别。

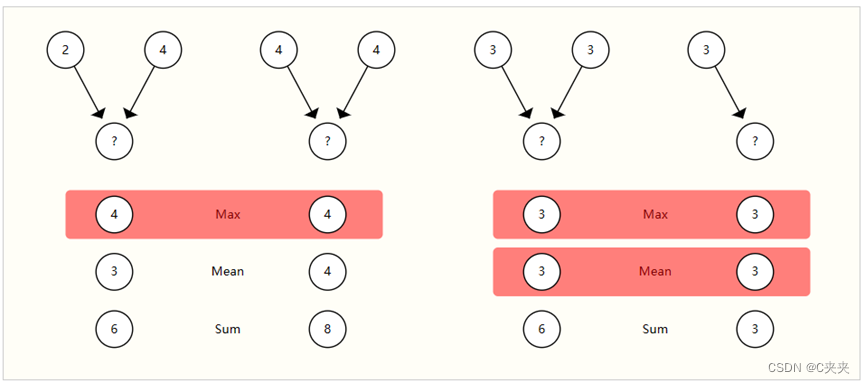
没有池化类型可以始终区分图形对，例如左侧的最大池化和右侧的总和/均值池化。
没有一种操作是统一的最佳选择。当节点具有高度可变的相邻要素数量，或者您需要局部邻域要素的规范化视图时，均值运算可能很有用。当您想要突出显示局部邻域中的单个显著特征时，最大运算可能很有用。Sum 通过提供要素局部分布的快照，在这两者之间实现了平衡，但由于它未归一化，因此还可以突出显示异常值。在实践中，总和是常用的。
设计聚合操作是一个开放的研究问题，与集合上的机器学习相交。新方法（如主邻域聚合）考虑了多个聚合操作，方法是将它们连接起来，并添加一个缩放函数，该函数取决于要聚合的实体的连通程度。同时，还可以设计特定于域的聚合操作。一个例子是“四面体手性”聚合算子。

4.5 GCN 作为子图函数逼近器

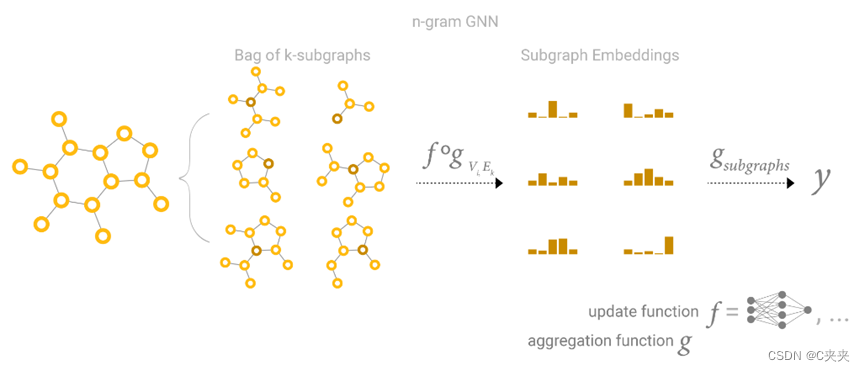
使用 1 度邻域查找查看 k 层的 GCN（和 MPNN）的另一种方法是作为神经网络，它对大小为 k 的子图的学习嵌入进行操作。
每一个点都是看以自己为中心的子图的汇聚。
当关注一个节点时，在 k 层之后，更新的节点表示具有所有相邻节点的有限视点，直到 k 距离，本质上是子图表示。边表示也是如此。
因此，GCN 正在收集所有可能的大小为 k 的子图，并从单个节点或边的有利位置学习向量表示。可能的子图的数量可以组合增长，因此从一开始就枚举这些子图，而不是像在 GCN 中那样动态构建它们，可能会令人望而却步。

4.6 边和图形对偶

需要注意的一点是，边缘预测和节点预测虽然看似不同，但往往会归结为同一个问题：图上的边缘预测任务G可以表述为节点级别的预测G的双重。
要获得G的对偶，我们可以将节点转换为边（边到节点）。图和它的对偶包含相同的信息，只是以不同的方式表示。有时，此属性使得在一种表示中比在另一种表示中更容易解决问题，例如傅里叶空间中的频率。简而言之，要解决一个边缘分类问题G，我们可以考虑在G的对偶（这与学习边表示相同G），这个想法是用双原始图卷积网络发展起来的。
图形卷积作为矩阵乘法，矩阵乘法作为图形上的游走
核心思想：在图上做卷积等价于把它拿出来做一个矩阵的乘法

4.7 图形注意力网络

在图上权重对于位置是不敏感的，权重取决于两个顶点向量之间的关系，
在图形属性之间传递信息的另一种方式是通过注意力。

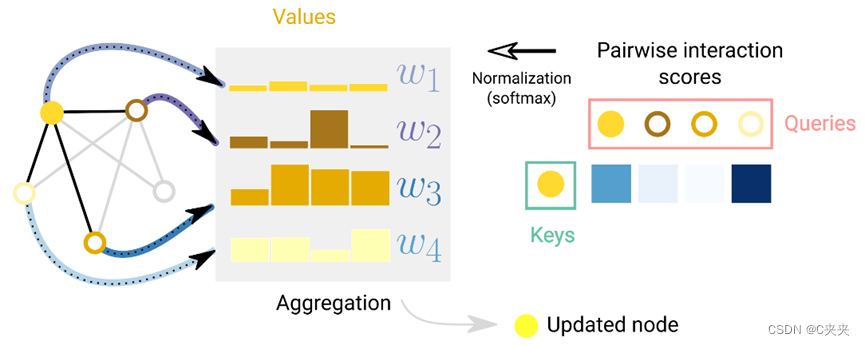
一个节点相对于其相邻节点的注意力示意图。对于每条边，都会计算、归一化交互分数，并用于对节点嵌入进行加权。
此外，转换器可以看作是具有注意力机制的GNN。在这种观点下，转换器将多个元素（即字符标记）建模为全连接图中的节点，注意力机制为每个节点对分配边缘嵌入，用于计算注意力权重。区别在于实体之间假定的连接模式，GNN假设稀疏模式，而Transformer则对所有连接进行建模。

4.8 图表解释和归因

在野外部署GNN时，我们可能会关心模型的可解释性，以建立可信度、调试或科学发现。我们关心解释的图形概念因上下文而异。例如，对于分子，我们可能会关心特定子图的存在与否，而在引文网络中，我们可能会关心文章的连通程度。由于图形概念的多样性，有许多方法可以构建解释。GNNExplainer 将这个问题视为提取对任务很重要的最相关的子图。归因技术将排名重要性值分配给图中与任务相关的部分。由于可以综合生成现实且具有挑战性的图问题，因此 GNN 可以作为评估归因技术的严格且可重复的测试平台。

图形上一些可解释性技术的示意图。归因将排名值分配给图形属性。排名可以用作提取可能与任务相关的连接子图的基础。

4.9 生成式建模

除了学习图上的预测模型外，我们可能还关心学习图的生成模型。使用生成模型，我们可以通过从学习的分布中采样或通过完成给定起点的图形来生成新图形。相关应用是新药的设计，其中需要具有特定特性的新型分子图作为治疗疾病的候选药物。另一种方法是按顺序构建图，方法是从图开始，然后迭代应用离散操作，例如节点和边的加法或减法。为了避免估计离散操作的梯度，我们可以使用策略梯度。这是通过自回归模型（如RNN）或在强化学习场景中完成的。此外，有时图形可以建模为仅具有语法元素的序列。

5 参考文献

A gentle introduction to Graph Neural Networks

1. Understanding Convolutions on Graphs
   Daigavane, A., Ravindran, B. and Aggarwal, G., 2021. Distill. DOI: 10.23915/distill.00032
2. The Graph Neural Network Model
   Scarselli, F., Gori, M., Tsoi, A.C., Hagenbuchner, M. and Monfardini, G., 2009. IEEE Transactions on Neural Networks, Vol 20(1), pp.
3. A Deep Learning Approach to Antibiotic Discovery
   Stokes, J.M., Yang, K., Swanson, K., Jin, W., Cubillos-Ruiz, A., Donghia, N.M., MacNair, C.R., French, S., Carfrae, L.A., Bloom-Ackermann, Z., Tran, V.M., Chiappino-Pepe, A., Badran, A.H., Andrews, I.W., Chory, E.J., Church, G.M., Brown, E.D., Jaakkola, T.S., Barzilay, R. and Collins, J.J., 2020. Cell, Vol 181(2), pp. 475–483.
4. Learning to simulate complex physics with graph networks
   Sanchez-Gonzalez, A., Godwin, J., Pfaff, T., Ying, R., Leskovec, J. and Battaglia, P.W., 2020.
5. Fake News Detection on Social Media using Geometric Deep Learning
   Monti, F., Frasca, F., Eynard, D., Mannion, D. and Bronstein, M.M., 2019.
6. Traffic prediction with advanced Graph Neural Networks
   *, O.L. and Perez, L…
7. Pixie: A System for Recommending 3+ Billion Items to 200+ Million Users in {Real-Time}
   Eksombatchai, C., Jindal, P., Liu, J.Z., Liu, Y., Sharma, R., Sugnet, C., Ulrich, M. and Leskovec, J., 2017.
8. Convolutional Networks on Graphs for Learning Molecular Fingerprints
   Duvenaud, D., Maclaurin, D., Aguilera-Iparraguirre, J., Gomez-Bombarelli, R., Hirzel, T., Aspuru-Guzik, A. and Adams, R.P., 2015.
9. Distributed Representations of Words and Phrases and their Compositionality
   Mikolov, T., Sutskever, I., Chen, K., Corrado, G. and Dean, J., 2013.
10. BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding
    Devlin, J., Chang, M., Lee, K. and Toutanova, K., 2018.
11. Glove: Global Vectors for Word Representation
    Pennington, J., Socher, R. and Manning, C., 2014. Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP).
12. Learning to Represent Programs with Graphs
    Allamanis, M., Brockschmidt, M. and Khademi, M., 2017.
13. Deep Learning for Symbolic Mathematics
    Lample, G. and Charton, F., 2019.
14. KONECT
    Kunegis, J., 2013. Proceedings of the 22nd International Conference on World Wide Web - WWW '13 Companion.
15. An Information Flow Model for Conflict and Fission in Small Groups
    Zachary, W.W., 1977. J. Anthropol. Res., Vol 33(4), pp. 452–473. The University of Chicago Press.
16. Learning Latent Permutations with Gumbel-Sinkhorn Networks
    Mena, G., Belanger, D., Linderman, S. and Snoek, J., 2018.
17. Janossy Pooling: Learning Deep Permutation-Invariant Functions for Variable-Size Inputs
    Murphy, R.L., Srinivasan, B., Rao, V. and Ribeiro, B., 2018.
18. Neural Message Passing for Quantum Chemistry
    Gilmer, J., Schoenholz, S.S., Riley, P.F., Vinyals, O. and Dahl, G.E., 2017. Proceedings of the 34th International Conference on Machine Learning, Vol 70, pp. 1263–1272. PMLR.
19. Relational inductive biases, deep learning, and graph networks
    Battaglia, P.W., Hamrick, J.B., Bapst, V., Sanchez-Gonzalez, A., Zambaldi, V., Malinowski, M., Tacchetti, A., Raposo, D., Santoro, A., Faulkner, R., Gulcehre, C., Song, F., Ballard, A., Gilmer, J., Dahl, G., Vaswani, A., Allen, K., Nash, C., Langston, V., Dyer, C., Heess, N., Wierstra, D., Kohli, P., Botvinick, M., Vinyals, O., Li, Y. and Pascanu, R., 2018.
20. Deep Sets
    Zaheer, M., Kottur, S., Ravanbakhsh, S., Poczos, B., Salakhutdinov, R. and Smola, A., 2017.
21. Molecular graph convolutions: moving beyond fingerprints
    Kearnes, S., McCloskey, K., Berndl, M., Pande, V. and Riley, P., 2016. J. Comput. Aided Mol. Des., Vol 30(8), pp. 595–608.
22. Feature-wise transformations
    Dumoulin, V., Perez, E., Schucher, N., Strub, F., Vries, H.d., Courville, A. and Bengio, Y., 2018. Distill, Vol 3(7), pp. e11.
23. Leffingwell Odor Dataset
    Sanchez-Lengeling, B., Wei, J.N., Lee, B.K., Gerkin, R.C., Aspuru-Guzik, A. and Wiltschko, A.B., 2020.
24. Machine Learning for Scent: Learning Generalizable Perceptual Representations of Small Molecules
    Sanchez-Lengeling, B., Wei, J.N., Lee, B.K., Gerkin, R.C., Aspuru-Guzik, A. and Wiltschko, A.B., 2019.
25. Benchmarking Graph Neural Networks
    Dwivedi, V.P., Joshi, C.K., Laurent, T., Bengio, Y. and Bresson, X., 2020.
26. Design Space for Graph Neural Networks
    You, J., Ying, R. and Leskovec, J., 2020.
27. Principal Neighbourhood Aggregation for Graph Nets
    Corso, G., Cavalleri, L., Beaini, D., Lio, P. and Velickovic, P., 2020.
28. Graph Traversal with Tensor Functionals: A Meta-Algorithm for Scalable Learning
    Markowitz, E., Balasubramanian, K., Mirtaheri, M., Abu-El-Haija, S., Perozzi, B., Ver Steeg, G. and Galstyan, A., 2021.
29. Graph Neural Tangent Kernel: Fusing Graph Neural Networks with Graph Kernels
    Du, S.S., Hou, K., Poczos, B., Salakhutdinov, R., Wang, R. and Xu, K., 2019.
30. Representation Learning on Graphs with Jumping Knowledge Networks
    Xu, K., Li, C., Tian, Y., Sonobe, T., Kawarabayashi, K. and Jegelka, S., 2018.
31. Neural Execution of Graph Algorithms
    Velickovic, P., Ying, R., Padovano, M., Hadsell, R. and Blundell, C., 2019.
32. Graph Theory
    Harary, F., 1969.
33. A nested-graph model for the representation and manipulation of complex objects
    Poulovassilis, A. and Levene, M., 1994. ACM Transactions on Information Systems, Vol 12(1), pp. 35–68.
34. Modeling polypharmacy side effects with graph convolutional networks
    Zitnik, M., Agrawal, M. and Leskovec, J., 2018. Bioinformatics, Vol 34(13), pp. i457–i466.
35. Machine learning in chemical reaction space
    Stocker, S., Csanyi, G., Reuter, K. and Margraf, J.T., 2020. Nat. Commun., Vol 11(1), pp. 5505.
36. Graphs and Hypergraphs
    Berge, C., 1976. Elsevier.
37. HyperGCN: A New Method of Training Graph Convolutional Networks on Hypergraphs
    Yadati, N., Nimishakavi, M., Yadav, P., Nitin, V., Louis, A. and Talukdar, P., 2018.
38. Hierarchical Message-Passing Graph Neural Networks
    Zhong, Z., Li, C. and Pang, J., 2020.
39. Little Ball of Fur
    Rozemberczki, B., Kiss, O. and Sarkar, R., 2020. Proceedings of the 29th ACM International Conference on Information & Knowledge Management.
40. Sampling from large graphs
    Leskovec, J. and Faloutsos, C., 2006. Proceedings of the 12th ACM SIGKDD international conference on Knowledge discovery and data mining - KDD '06.
41. Metropolis Algorithms for Representative Subgraph Sampling
    Hubler, C., Kriegel, H., Borgwardt, K. and Ghahramani, Z., 2008. 2008 Eighth IEEE International Conference on Data Mining.