本文主要是介绍最短路径(dijstra算法,链式前向星,堆优化),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
【模板】单源最短路径(弱化版)

对于这题我们使用邻接矩阵的话会导致弓箭复杂度会大大提升,所以我们就需要学习一种新的数据结构,名叫链式前向星,在链式前向星中,我们需要定义一个结构体数组,其中有成员to,w,next;
struct EGDE
{int to;//终点,仅仅是指两个点之间int w;//权值,路径长度int next;//指向前一个点
}edge[maxn];
int first[maxn];接下来构造存放边的函数,姑且叫做cinn函数
请大家将first数组想象成一个一个鞭子的把,next想象成鞭子的每一节,那么这个数组就可以按照鞭子的样子将所有边的信息存起来了。其实这个就是邻接表的升级版
void cinn(int u,int w,int v)//w代表着权值,u代表着first数组的下标,v代表着终点
{cnt++;//代表着下标,这个下标指的是边的下标edge[cnt].to=v;edge[cnt].w=w;edge[cnt].next=first[u];first[u]=cnt;
}接下来就是在主函数的输入的问题
cin>>n>>m;//n代表着节点数,m代表着边数for(int i=1;i<=m;i++){int u,v,w;cin>>u>>v>>w;//u代表着fisrt数组的下标,其中存放的值就是相当于这个鞭子的把,同时也是代表着起点cinn(u,v,w);//v代表着终点,w代表着权值cinn(v,u,w);//如果是有向边则只需要一个这样的函数,如果是无向边那么就需要写两个这样的函数}如何遍历这个鞭子呢,我们设计一个vis函数用于遍历,优势链式储存所以就需要将把拿到手,那么这个把就是出差呢在first数组里面,我们只需要将我们需要查找的链子的下标输进去即可
void vis(u)
{for(int i=first[u];i!=0;i=edge[i].next)//i的变化里面的i就是相当于first[u]{printf("%d--%d:%d\n",u,edge[i].to,edge[i].w);}
}前向链式星结构的最终代码
#include<iostream>
#define N 10000
using namespace std;
int cnt = 0;
struct EGDE
{int to;//终点,仅仅是指两个点之间int w;//权值,路径长度int next;//指向前一个点
}edge[N];
int first[N];
int n, m;
void cinn(int u, int v, int w)//w代表着权值,u代表着first数组的下标,v代表着终点
{cnt++;//代表着下标,这个下标指的是边的下标edge[cnt].to = v;edge[cnt].w = w;edge[cnt].next = first[u];first[u] = cnt;
}
void vis(int u)
{for (int i = first[u]; i != 0; i = edge[i].next)//i的变化里面的i就是相当于first[u]{printf("%d--%d:%d\n", u, edge[i].to, edge[i].w);}
}
int main()
{cin >> n >> m;//n代表着节点数,m代表着边数int s;cin>>s;for (int i = 1; i <= m; i++){int u, v, w;cin >> u >> v >> w;//u代表着fisrt数组的下标,其中存放的值就是相当于这个鞭子的把,同时也是代表着起点cinn(u, v, w);//v代表着终点,w代表着权值}vis(s);return 0;
}最后我们按照dijkstra算法的思路走一遍代码就可以出来了
#include<iostream>
#define N 1000000
using namespace std;
int cnt = 0;
long long ans[N];
bool book[N];
int first[100000];
int n,m,s;
struct EGDE
{int to;//终点,仅仅是指两个点之间int w;//权值,路径长度int next;//指向前一个点
}edge[N];
void cinm(int u, int v, int w)//w代表着权值,u代表着first数组的下标,v代表着终点
{//代表着下标,这个下标指的是边的下标edge[++cnt].to = v;edge[cnt].w = w;edge[cnt].next = first[u];first[u] = cnt;
}
int main()
{cin >> n >> m>>s;//n代表着节点数,m代表着边数for(int i=1;i<=m;i++)//将每一条边都设置为是最大值{ans[i]=2147483647;}ans[s]=0;//由于是从s开始所以要将着一条边设置为0方便结束for (int i = 1; i <= m; i++){int u, v, w;cin >> u >> v >> w;//u代表着fisrt数组的下标,其中存放的值就是相当于这个鞭子的把,同时也是代表着起点cinm(u, v, w);//v代表着终点,w代表着权值}int tmp=s;while(book[tmp]==0){long long minn=2147483647;book[tmp]=1;//将已经收录过的边进行标记//Dijkstra算法的核心部分for(int i=first[tmp];i!=0;i=edge[i].next)//这个就相当于遍历已经理解起来的点{if(!book[edge[i].to]&&ans[edge[i].to]>ans[tmp]+edge[i].w)//如果没有被标记且直接的两点距离大于通过某点的距离{ans[edge[i].to]=ans[tmp]+edge[i].w;//ans数组存放的是s点到ans下标编号的这个点的最短距离,其实这里优点像动态规划}}for(int i=1;i<=n;i++)//重新遍历全部点,找到没有被标记且最小的边{if(book[i]==0&&ans[i]<minn){minn=ans[i];//这个是为找到目前情况的最小值(每次寻找都有可能找到不同的最小边)tmp=i;//这个算法下一次就从这个最小边开始(由于这个是最小便已经确定,所以可以依赖这个节点进行下移的寻找)}}}for(int i=1;i<=n;i++){cout<<ans[i]<<" ";}return 0;
}dijkstra算法的核心两步:第一找出里目的地的最近的点(没有被收录的点之中),并将该点收录,下一次循环就从这个点开始。
第二判断这个点的距离是比从前面那个点加上前面那个点到这个点的距离谁大谁小,将小的距离重新赋给该值(动态规划的思路)。
【模板】单源最短路径(标准版)
这一题还得是用堆优化
1.这里要用到一个优先队列(stl),其本质就是用一个数组模拟的一个完全二叉树。
2.功能:拿出优先级最大的元素,这个优先级可以自己定义。
3.这个包括在头文件#include<queue>之中。
4.定义方式:priority_queue<int> que 尖括号说明里面存放的数是整型(这样定义就是大顶堆 值越大优先级越高)
5.关于优先队列的几种操作:1.que.size() 得到这个队列的元素数量
2.que.push(x) 插入
3.que.pop() 删除优先级最高的元素(弹出堆顶元素)
4.que.top()访问优先级最高的元素(访问堆顶元素)
5.que.empty()判断堆是否为空
插入删除的时间复杂空间度都是为对数级,访问堆顶元素的时间复杂度为常数级别。
接下俩是堆优先队列的一些基础操作
#include<iostream>
#include<queue>
#include<algorithm>
using namespace std;
int main()
{priority_queue<int> que;que.push(7);que.push(1);que.push(12);printf("nmber:");cout<<que.size()<<endl;while(!que.empty()){cout<<que.top()<<endl;que.pop();}cout<<endl;return 0;
}输出数据如下(这样就可以使用堆排序)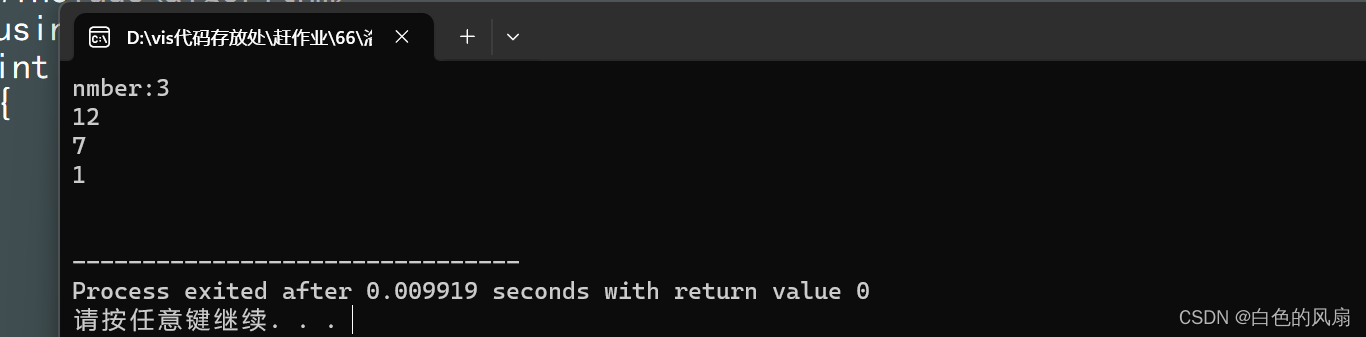
在优先队列中其实有三个参量,第一是选择的类型,第二就是我们可以选择的容器,我们课以放一个vector<int>来表示一维数组,第三个参数就是我们的自定义如less<int>就表示大顶,greater<int>就表示小顶对(我没想到这个竟然是反着来的)
priority_queue<int,vector<int>,greater<int>>//从小到大对于我们自定义
#include<iostream>
#include<queue>
#include<algorithm>
using namespace std;
struct node
{int x,y;bool operator< (const node &b) const{//运算符重新定义,注意这个运算符只能定义小于号return this->x>b.x;//从大到小}
};int main()
{priority_queue<node> que;que.push((node){5,2});que.push((node){2,4});while(!que.empty()){cout<<que.top().x<<endl;que.pop();}return 0;
}输出结果: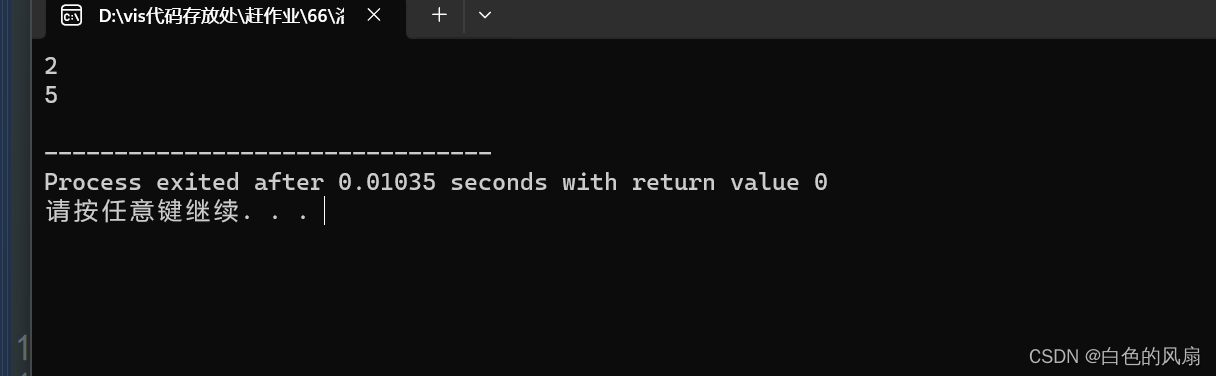
在我们用基础的模板时,都会用到for循环来找到最小值(也就是打擂台的方法),但是这样就会导致时间超限,而堆每次的堆顶都是小顶堆,这样就免去了找到最小值的步骤从而减少对时间的开销。

那么有关最短路径问题我们以后就需要知道以下三点:1.对于最短路径问题我们需要使用dijstra算法 2.在dijstra算法中我们需要用到小顶堆来存放每一次的最小值。 3.我们需要使用链式前向星来存放边的信息。
对于dijstra算法核心步骤:1.遍历与目标点相连的所有点,将其举止都更新。2.找出最小值并将其标记为以收入状态,直到所有点都已经全部标记。
代码如下:
#include<iostream>
#include<queue>
using namespace std;
const int maxN = 100010;
const int maxM = 500010;
int n, m, s, cnt;
struct node
{int id;int dis;bool operator< (const node& x) const {return x.dis < dis;}
};
priority_queue<node> q;
struct EDGE
{int to;int w;int next;
}edge[maxM];
int head[maxM];
bool vis[maxM];
int ans[maxM];
void add(int u, int v, int w)
{cnt++;edge[cnt].to = v;edge[cnt].w = w;edge[cnt].next = head[u];head[u] = cnt;
}
int main()
{cin >> n >> m >> s;for (int i = 1; i <= m; i++){int u, v, w;cin >> u >> v >> w;add(u, v, w);}for (int i = 1; i <= maxM; i++){ans[i] = 0x7fffffff;}ans[s]=0;q.push(node{s,0});while(!q.empty()){node tmp=q.top();q.pop();int k=tmp.id;if(vis[k])continue;vis[k]=true;for(int i=head[k];i!=0;i=edge[i].next){int to=edge[i].to;if(!vis[to]&&ans[to]>ans[k]+edge[i].w){ans[to]=ans[k]+edge[i].w;q.push(node{to,ans[to]});}}}for (int i = 1; i <= n; i++){cout << ans[i] << " ";}return 0;
}这篇关于最短路径(dijstra算法,链式前向星,堆优化)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






