1.合唱队形

本文主要是介绍1.合唱队形，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

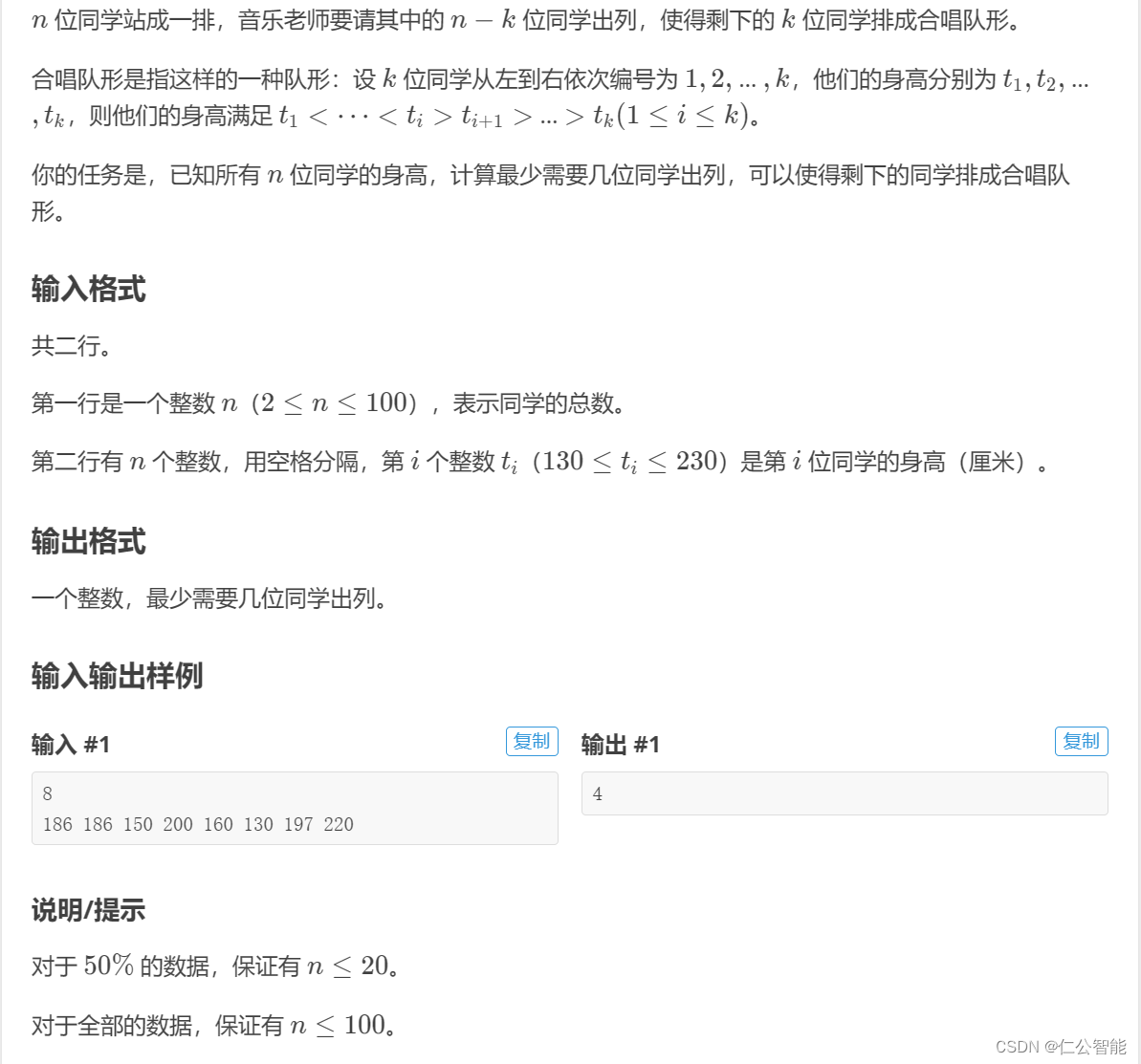
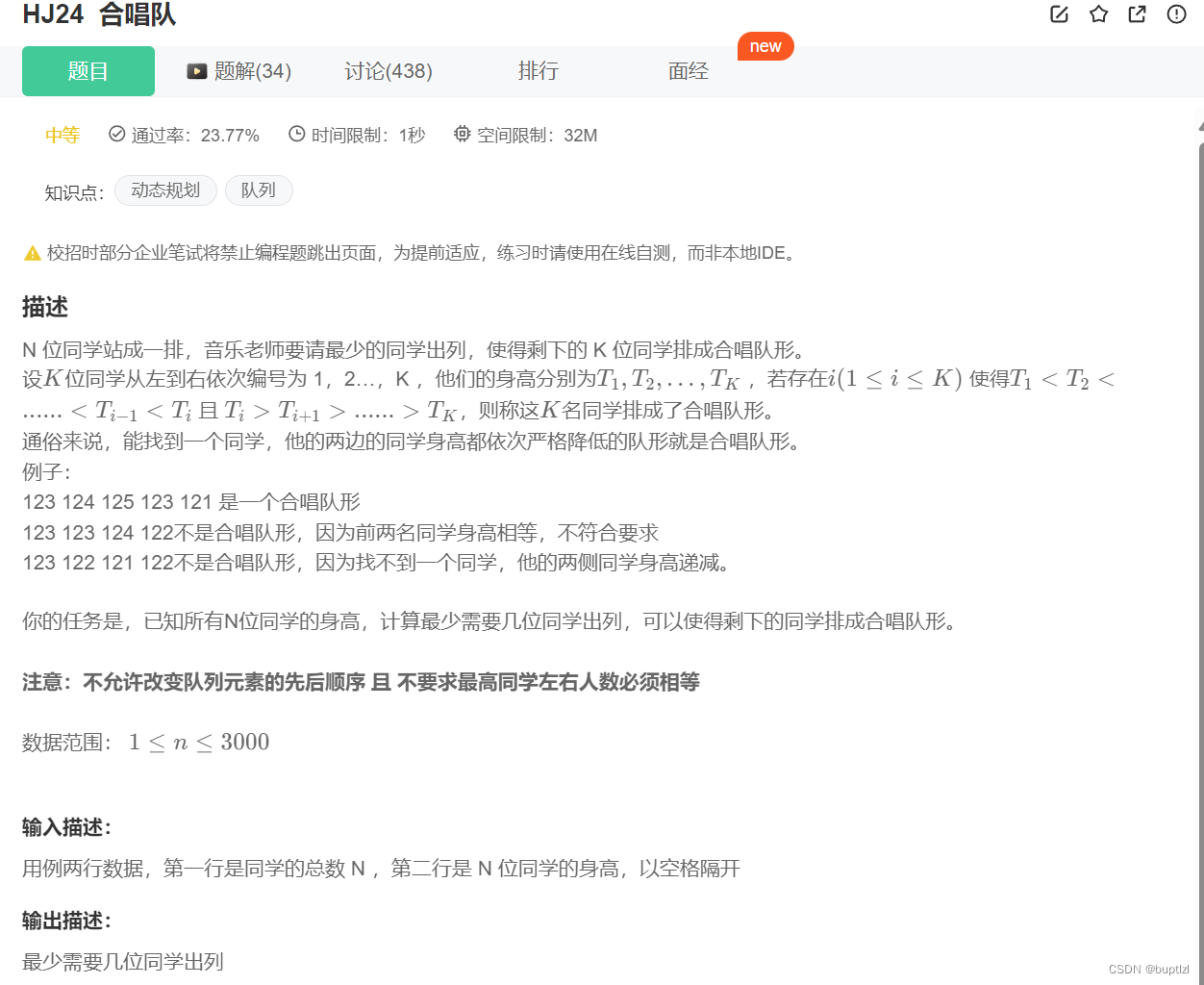
Problem: 1.合唱队形

思路

这是一个动态规划问题。我们可以通过两次动态规划来解决这个问题。首先，我们从左到右进行动态规划，计算出每个位置的最长递增子序列长度。然后，我们从右到左进行动态规划，计算出每个位置的最长递减子序列长度。最后，我们遍历每个位置，找出最长递增子序列长度和最长递减子序列长度之和最大的位置，这个位置就是合唱队形的中心位置。然后，我们计算出需要出列的同学数量，即总人数减去最长递增子序列长度和最长递减子序列长度之和再加一。

解题方法

1、初始化两个数组，一个用来存储从左到右的最长递增子序列长度，一个用来存储从右到左的最长递减子序列长度。
2、从左到右进行动态规划，计算出每个位置的最长递增子序列长度。
3、从右到左进行动态规划，计算出每个位置的最长递减子序列长度。
4、遍历每个位置，找出最长递增子序列长度和最长递减子序列长度之和最大的位置。
5、计算出需要出列的同学数量，即总人数减去最长递增子序列长度和最长递减子序列长度之和再加一。

复杂度

时间复杂度:

这个算法的时间复杂度是$O(n^2)$，因为我们需要进行两次动态规划，每次动态规划的时间复杂度都是$O(n^2)$。

空间复杂度:

这个算法的空间复杂度是$O(n)$，因为我们需要存储两个长度为n的数组。

Code

import java.util.*;
import java.io.*;
// 1:无需package
// 2: 类名必须Main, 不可修改public class Main {static BufferedReader in = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static StreamTokenizer sr = new StreamTokenizer(in);static int n;static int MAXN = 110;static int[] arr = new int[MAXN];static int[] dpl = new int[MAXN];static int[] dpr = new int[MAXN];public static void main(String[] args) throws IOException {n = nextInt();for(int i = 1; i <= n; i++) {arr[i] = nextInt();}for(int i = 1; i <= n; i++) {dpl[i] = 1;for(int j = 1; j < i; j++) {if(arr[i] > arr[j]) dpl[i] = Math.max(dpl[i], dpl[j] + 1);}}for(int i = n; i >= 1; i--) {dpr[i] = 1;for(int j = i + 1; j <= n; j++) {if(arr[i] > arr[j]) dpr[i] = Math.max(dpr[i], dpr[j] + 1);}}int ans = n;for(int i = 1; i <= n; i++) {ans = Math.min(ans, n - (dpl[i] + dpr[i] - 1));}out.println(ans);out.flush();}static int nextInt() throws IOException {sr.nextToken();return (int)sr.nval;}
}

这篇关于1.合唱队形的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---