本文主要是介绍线性代数笔记9——消元矩阵与置换矩阵,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
消元矩阵
如果用矩阵表示一个有解的方程组,那么矩阵经过消元后,最终能变成一个上三角矩阵U。用一个三元一次方程组举例:

A经过一些列变换,最终得到了一个上三角矩阵U:
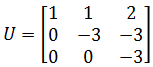
回代到方程组后可以直接求解:
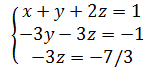
如果上面的变换去掉增广矩阵,可以简写为:
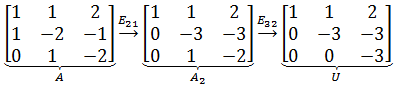
矩阵的初等变换可以用矩阵乘法实现,现在的问题是,我们能否得到一个可以表示整个消元过程的矩阵E,使得E与A相乘能够直接得到U?还是以上面的矩阵为例,第一次变换是用第二行加上第一行的-1倍,所以只需将A的左边乘以E21就可以:
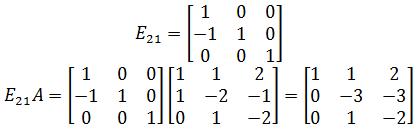
这里的矩阵E21又是怎么来的呢?这需要回归一下消元的过程:
首先,A的第一行不变,因此我们需要拿出A的1个第一行,0个第二行,0个第三行,于是(1 ,0, 0)组成了E21的第一行;
然后,我们需要-1个A的第一行,1个第二行,0个第三行进行线性组合,所以(-1, 1, 0)组成了E21的第二行;
最后,因为A的第三行不变,因此需要0个第一行,0个第二行,1个第三行,所以E21的第三行是(0, 0, 1)。
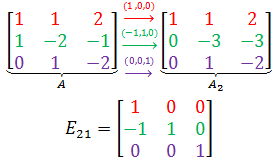
经过变换,得到了A2,可以用E21A = A2表示。A2继续变换:
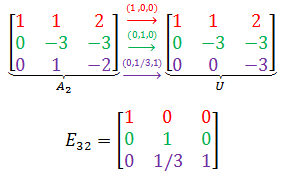
最终,E32(E21A ) = (E32E21)A = U,E = E32E21
置换矩阵
同样可以使用矩阵相乘来完成行交换和列交换。
首先是行交换,对矩阵进行如下变换:

对于A2的第一行,相当于从A中拿出了0个第一行,1个第二行,0个第三行;
对于A2的第二行,相当于从A中拿出了1个第一行,0个第二行,0个第三行;
对于A2的第三行,相当于从A中拿出了0个第一行,0个第二行,1个第三行。

上面的P12称为行置换矩阵。可以看出置换矩阵是一个每行只有一个维度是1的满秩矩阵,或者说是行重新排列了的单位矩阵,它的一个特性是 P-1 = PT
行交换与行交换类似,但是需要将左乘变为右乘。
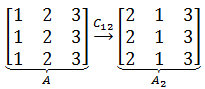
对于A2的第一列,相当于从A中拿出了0个第一列,1个第二列,0个第三列;
对于A2的第二列,相当于从A中拿出了1个第一列,0个第二列,0个第三列;
对于A2的第三列,相当于从A中拿出了0个第一列,0个第二列,1个第三列。

C12称为列置换矩阵。注意列置换矩阵的结果,是按照列构成的。
作者:我是8位的
出处:http://www.cnblogs.com/bigmonkey
本文以学习、研究和分享为主,如需转载,请联系本人,标明作者和出处,非商业用途!
扫描二维码关注公众号“我是8位的”

这篇关于线性代数笔记9——消元矩阵与置换矩阵的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





