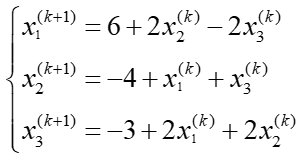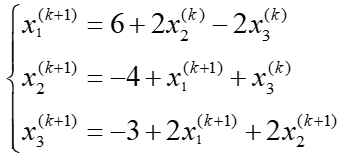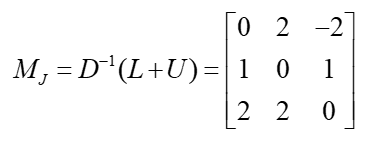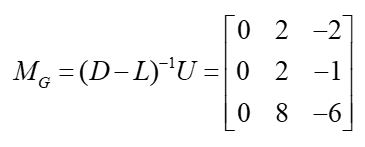计算方法（二）线性代数方程组的数值解

1. 高斯消元法

线性代数的知识，过于基础

2. 矩阵的三角分解

2.1 LU分解

主要记住，如何通过LU分解（包括接下来的杜利特尔分解也属于其中一种）来计算A$x$=b

四步法：
最初：A$x$=b
LU分解：LU$x$=b（这里分解方法看2.2）
求y：Ly=b
求x：Ux=y

2.2 杜利特尔分解

就是高斯消元的过程，每次消元的乘积数写在对应位置上得到L，高斯消元的结果是U，必考。题目一般要结合上述通过分解计算A$x$=b的方法。
下图第一行为LDU分解，第二行为克洛特分解。
挺简单的，稍微看一下就好。

LDU即在杜利特尔分解的基础上将按列再进行一次高斯消元得到D和U；克洛特分解即是在最初的矩阵按列进行一次高斯消元。

所以也可以说，杜利特尔分解是L(DU)，克洛特分解是(LD)U

3. 消元法在计算机上的实现

3.1选主元的必要性

看下书即可，大概写的是，主要是怕主元过小，放大倍数过高，误差一下就起来了。

3.2 选主元的方法

列主元：每次从主元所在的列里选最大的，然后将最大的这一行和本来主元所在行交换。

全主元：不考

4. 向量和矩阵范数

这一节一下子背的东西多起来了。

4.1 向量范数

定义

定义我扒百度了，注意其中||$x$||=0当且仅当$x$=0很重要，是判断一个函数是否可以是一个范数的充分条件。

性质

1. ||0||=0
2. ||-x||=|-1|*||x||=||x||
3. ||x-y||≥||x||-||y||

常见三种向量范数：1，2，∞

等价性

如果你愿意看，还可以看一下向量范数的等价性。

||$x$||${}_{\infty }$ ≤ ||$x$||${}_2$ ≤ $\sqrt{n}$*||$x$||${}_{\infty }$

||$x$||${}_{\infty }$ ≤ ||$x$||${}_1$ ≤ $n$*||$x$||${}_{\infty }$

我是觉得看不看都ok了

收敛性

划重点的时候强调了，收敛性也要会

收敛的充分条件：

收敛的充要条件：

4.2 矩阵范数

同样也是，正定性、齐次性、三角不等式三个性质，只不过矩阵用AB，向量用xy而已。

题里出过求矩阵范数，所以还是要记一下这些常见的矩阵范数。

4.3 谱半径

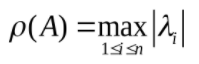
λ是A的特征值，谱半径就是求按模最大的特征值

P.S. 特征值概念来自线性代数，可以随便找个b站视频看一下特征值和特征向量，学习通资料里的视频有点抽象，适合理解数学，不太适合背计算。

重点： 对称矩阵的谱半径和其2范数相等

5.条件数

只需要知道条件数的定义：

cond(A)=||A||*||A${}^{-1}$||

（||是上面刚讲的范数）

6.迭代法

6.1 迭代法的一般形式

$x^{\ast }$ = M$x^{\ast }$ + g

从这个式子看起，我们要知道，迭代法里面所有公式，左面的x和右面的x不是一个x，左面的相当于$x^{(k+1)}$，右面的相当于$x^{(k)}$
我们不停的带入$x^{(k)}$求得$x^{(k+1)}$，使x越趋向于真实解，所以，我们需要找到一个收敛的迭代格式。

6.2 迭代法的收敛性

这两个定义还是挺重要的，划重点的时候特意说了一下。

定理2.7 迭代格式对任何初始近似值$x^{(0)}$均收敛的充要条件是迭代矩阵M得谱半径ρ(M)<1

推论2.1 若||M||<1（可以是任何一种相容范数），则迭代格式收敛。

6.3 雅各比迭代法

6.4 高斯-赛德尔迭代法

这两个一起说了，根据P49页例题讲。

分别用其他变量表示x,y,z（各个不同的变量），根据各个迭代法得分量形式用于计算。

雅各比：左侧为第(k+1)代，右侧为第(k)代。

高斯：左侧为第(k+1)代，右侧若已经算出，则用刚刚算出的第(k+1)代，否则为第(k)代。

迭代法的矩阵形式判断迭代法是否收敛：

首先要记住三个变量，虽然与之前矩阵分解的变量同名，但是不同含义，首先，最基础的矩阵（根据题中得到的）定义为A。

D：A的对角线构成的对角矩阵
-L：A的严格下三角部分构成的下三角矩阵
-U：A的严格上三角部分构成的上三角矩阵

什么叫严格：就是主对角线全是0

然后要记住分别的迭代矩阵：

雅各比：

高斯：

求M矩阵的特征值（线代），按模（实数就是绝对值）最大的特征值是谱半径（上文4.3），谱半径<1就收敛（上文6.2）。

这道题还是挺重要的，相当于把之前的知识点都套进来了，而且考试也有只改个数的一样的题。