本文主要是介绍C#,最大公共子序列(LCS,Longest Common Subsequences)的算法与源代码,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
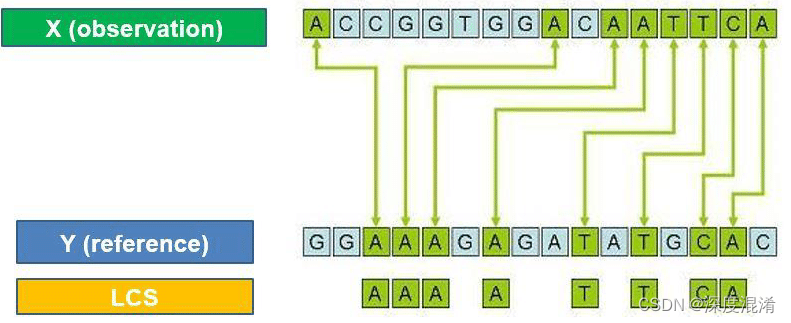
1 最大公共子序列
最长的常见子序列问题是寻找两个给定字符串中存在的最长序列。
最大公共子序列算法,常用于犯罪鉴定、亲子鉴定等等的 DNA 比对。
1.1 子序列
让我们考虑一个序列S=<s1,s2,s3,s4,…,sn>。
一个序列Z=<z1,z2,z3,z4,…,zm>在S上被称为S的子序列,当且仅当它可以从某些元素的S删除中派生出来时。
1.2 公共子序列
假设X和Y是有限元素集上的两个序列。如果Z是X和Y的子序列,我们可以说Z是X和Y的公共子序列。
1.3 最长公共子序列
如果给定一组序列,则最长公共子序列问题是找到所有序列中具有最大长度的公共子序列。
最长的常见子序列问题是一个经典的计算机科学问题,是diff实用程序等数据比较程序的基础,在生物信息学中有应用。它还被SVN和Git等版本控制系统广泛用于协调对受版本控制的文件集合所做的多个更改。
2 递归算法源程序
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class StringSearch
{
/// <summary>
/// 两个字符串的最大公共子字符串
/// </summary>
/// <param name="X"></param>
/// <param name="Y"></param>
/// <param name="m"></param>
/// <param name="n"></param>
/// <returns></returns>
public static int LCS_Solve(string X, string Y, int m, int n)
{
if (m == 0 || n == 0)
{
return 0;
}
if (X[m - 1] == Y[n - 1])
{
return 1 + LCS_Solve(X, Y, m - 1, n - 1);
}
else
{
return Math.Max(LCS_Solve(X, Y, m, n - 1), LCS_Solve(X, Y, m - 1, n));
}
}
}
}
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;namespace Legalsoft.Truffer.Algorithm
{public static partial class StringSearch{/// <summary>/// 两个字符串的最大公共子字符串/// </summary>/// <param name="X"></param>/// <param name="Y"></param>/// <param name="m"></param>/// <param name="n"></param>/// <returns></returns>public static int LCS_Solve(string X, string Y, int m, int n){if (m == 0 || n == 0){return 0;}if (X[m - 1] == Y[n - 1]){return 1 + LCS_Solve(X, Y, m - 1, n - 1);}else{return Math.Max(LCS_Solve(X, Y, m, n - 1), LCS_Solve(X, Y, m - 1, n));}}}
}3 非递归算法源程序
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
public static partial class StringSearch
{
/// <summary>
/// 计算两个字符串的最大公共子字符串
/// </summary>
/// <param name="X"></param>
/// <param name="Y"></param>
/// <returns></returns>
public static int LCS_Solve(string X, string Y)
{
int m = X.Length;
int n = Y.Length;
int[,] LengthArray = new int[m + 1, n + 1];
for (int i = 0; i <= m; i++)
{
for (int j = 0; j <= n; j++)
{
if (i == 0 || j == 0)
{
LengthArray[i, j] = 0;
}
else if (X[i - 1] == Y[j - 1])
{
LengthArray[i, j] = LengthArray[i - 1, j - 1] + 1;
}
else
{
LengthArray[i, j] = Math.Max(LengthArray[i - 1, j], LengthArray[i, j - 1]);
}
}
}
return LengthArray[m, n];
}
}
}
——————————————————————————
POWER BY TRUFFER.CN 50018.COM
using System;
using System.Text;
using System.Collections;
using System.Collections.Generic;namespace Legalsoft.Truffer.Algorithm
{public static partial class StringSearch{/// <summary>/// 计算两个字符串的最大公共子字符串/// </summary>/// <param name="X"></param>/// <param name="Y"></param>/// <returns></returns>public static int LCS_Solve(string X, string Y){int m = X.Length;int n = Y.Length;int[,] LengthArray = new int[m + 1, n + 1];for (int i = 0; i <= m; i++){for (int j = 0; j <= n; j++){if (i == 0 || j == 0){LengthArray[i, j] = 0;}else if (X[i - 1] == Y[j - 1]){LengthArray[i, j] = LengthArray[i - 1, j - 1] + 1;}else{LengthArray[i, j] = Math.Max(LengthArray[i - 1, j], LengthArray[i, j - 1]);}}}return LengthArray[m, n];}}
}这篇关于C#,最大公共子序列(LCS,Longest Common Subsequences)的算法与源代码的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








