本文主要是介绍伯恩赛德定理(集合S的 置换群 诱导出来的等价关系 对集合S 划分 得到的 等价类个数),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言:仅个人小记。这个定理就是用来计数的,用来数一数等价类的个数,而等价类本质上是一种降维表示,即把同种东西归类,进而达到简化的目的,进而更能凸现事物的本质。等价类的个数类似于线性代数里面 “秩” 这个概念,而不同的等价类则类似于不同的 “基向量” 。
前要知识和规定
1.由集合 S 上的一个置换群 < G , ∗ > <G,*> <G,∗>诱导的二元关系 R是一个等价关系 。证明参看 https://blog.csdn.net/qq_25847123/article/details/100253596
2. X a b X_{ab} Xab 表示所有将 a 置换成 b 的置换的集合。
伯恩赛德(Burnside)定理内容
由集合 S 上的一个置换群 < G , ∗ > <G,*> <G,∗>诱导的等价关系 R 将集合 S 划分所得到的等价类数目等于
1 ∣ G ∣ ∑ π ∈ G ψ ( π ) \frac{1}{|G|}\sum_{\pi\in G}\psi(\pi) ∣G∣1π∈G∑ψ(π) ψ ( π ) \psi(\pi) ψ(π)表示 在置换 π \pi π 作用下不变元个数。不变元指的是满足 π ( a ) = a \pi(a)=a π(a)=a 的元素 a 。
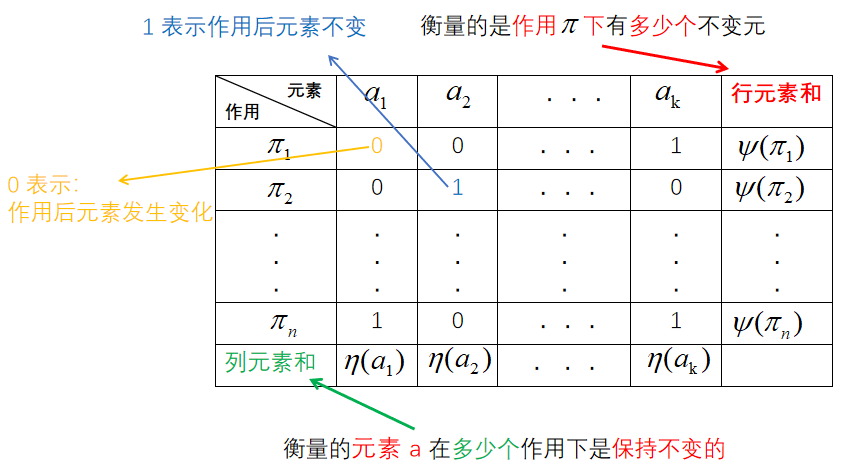
引入 η ( a ) \eta(a) η(a) 表示元素 a 在多少个作用下是保持不变的,由上图,显然有 ∑ π ∈ G ψ ( π ) = ∑ s ∈ S η ( s ) \sum_{\pi\in G}\psi(\pi)=\sum_{s\in S}\eta (s) π∈G∑ψ(π)=s∈S∑η(s) 所 有 行 和 的 总 和 = 所 有 列 和 的 总 和 所有行和的总和=所有列和的总和 所有行和的总和=所有列和的总和
故而, 想要求解等价类个数,只要数一数 G 中各个元素 π \pi π分别有多少个不变元,然后加起来,再除以置换群 G 的阶,就得到等价类的个数了。
定理证明
显然,证明 等 价 类 的 个 数 = 1 ∣ G ∣ ∑ π ∈ G ψ ( π ) 等价类的个数=\frac{1}{|G|}\sum_{\pi\in G}\psi(\pi) 等价类的个数=∣G∣1π∈G∑ψ(π)就等价于证明 等 价 类 的 个 数 = 1 ∣ G ∣ ∑ s ∈ S η ( s ) 等价类的个数=\frac{1}{|G|}\sum_{s\in S}\eta (s) 等价类的个数=∣G∣1s∈S∑η(s)
前要证明(1)
证明: 如果 a, b 同属一个等价类,则必然有且仅有 η ( a ) \eta(a) η(a) 个作用,使得 a 置换成 b。
记所有作用于 a 结果仍为 a 的作用为集合 X a a X_{aa} Xaa,该集合元素个数为 ∣ X a a ∣ = η ( a ) |X_{aa}|=\eta(a) ∣Xaa∣=η(a)。
因为 a, b 同属一个等价类,所以必然存在 π t \pi_t πt ,有 π t ( a ) = b \pi_t(a)=b πt(a)=b。用 π t \pi_t πt和集合 X a X_a Xa中的每个元素相乘,容易证明
π t ∗ π i = ̸ π t ∗ π j , i = ̸ j , π i , π j ∈ X a a \pi_t*\pi_i=\not\pi_t*\pi_j,i=\not j,\pi_i,\pi_j\in X_{aa} πt∗πi≠πt∗πj,i≠j,πi,πj∈Xaa故而, π t \pi_t πt和集合 X a a X_{aa} Xaa中的每个元素相乘结果互不相同,故而可以记为集合 X a b X_{ab} Xab,显然该集合元素个数为 ∣ X a b ∣ = ∣ X a a ∣ = η ( a ) |X_{ab}|=|X_{aa}|=\eta(a) ∣Xab∣=∣Xaa∣=η(a)。
X a b = { π ∣ π ( a ) = b , ∀ π ∈ X a a } X_{ab}=\{\pi|\pi(a)=b, \forall \pi \in X_{aa}\} Xab={π∣π(a)=b,∀π∈Xaa}显然,集合 X a b X_{ab} Xab中的每个元素都满足 π ( a ) = b , ∀ π ∈ X a b \pi(a)=b,\forall \pi\in X_{ab} π(a)=b,∀π∈Xab我们认为不可能再有其他的不属于集合 X a b X_{ab} Xab的作用 π k \pi_k πk 能够 π k ( a ) = b \pi_k(a)=b πk(a)=b。反证法如下:
假定
∃ π k ∈ ̸ X a b , 使 得 π k ( a ) = b \exist\pi_k\in\not X_{ab},使得\pi_k(a)=b ∃πk∉Xab,使得πk(a)=b则,因为这些元素都来自置换群 G,所以这些元素都可逆。进而取集合 X a b X_{ab} Xab中任一元素 π t \pi_t πt,则其逆元为
π t − 1 , 有 π t − 1 ( b ) = a {\pi_t}^{-1},有{\pi_t}^{-1}(b)=a πt−1,有πt−1(b)=a进而显然 π t − 1 ∗ π k ( a ) = π t − 1 ( b ) = a {\pi_t}^{-1}*\pi_k(a)={\pi_t}^{-1}(b)=a πt−1∗πk(a)=πt−1(b)=a又因为封闭性,所以
π t − 1 ∗ π k ∈ G {\pi_t}^{-1}*\pi_k\in G πt−1∗πk∈G又因为所有能够是的 a 仍作用为 a 的作用都在集合 X a a X_{aa} Xaa中,所以必然
π t − 1 ∗ π k ∈ X a {\pi_t}^{-1}*\pi_k\in X_a πt−1∗πk∈Xa进而 π k = π t ∗ ( π t − 1 ∗ π k ) ∈ X a b \pi_k=\pi_t*({\pi_t}^{-1}*\pi_k)\in X_{ab} πk=πt∗(πt−1∗πk)∈Xab与上述 π k ∈ ̸ X a b \pi_k\in\not X_{ab} πk∉Xab矛盾。故而不存在其他的作用能够使得 a 作用成 b,所以,所有的能够使得 a 作用成 b 的作用都在集合 X a b X_{ab} Xab中,故而,当 a, b 同属一个等价类时,必然有且仅有 η ( a ) \eta(a) η(a)个作用,使得 a 作用成 b。证毕!
正式证明
对于任意一个置换,必然将元素 a 置换成 a 所在等价类中的某个元素,假设 a 的等价类为 [a]={a,b,…,k},则
∣ X a a ∣ + ∣ X a b ∣ + . . . + ∣ X a k ∣ = ∣ G ∣ |X_{aa}|+|X_{ab}|+...+|X_{ak}|=|G| ∣Xaa∣+∣Xab∣+...+∣Xak∣=∣G∣又根据前要证明(1),知
η ( a ) = ∣ X a a ∣ = ∣ X a b ∣ = . . . = ∣ X a k ∣ \eta(a)=|X_{aa}|=|X_{ab}|=...=|X_{ak}| η(a)=∣Xaa∣=∣Xab∣=...=∣Xak∣进而
η ( a ) = η ( b ) = . . . = η ( k ) = ∣ G ∣ k \eta(a)=\eta(b)=...=\eta(k)=\frac{|G|}{k} η(a)=η(b)=...=η(k)=k∣G∣由于 a 是从 S 中任意选取的,根据上面知道, ∀ 等 价 类 [ a ] , ∑ s ∈ [ a ] η ( s ) = ∣ G ∣ \forall 等价类[a],\sum_{s\in[a]}\eta(s)=|G| ∀等价类[a],s∈[a]∑η(s)=∣G∣进而,如果有 p 个等价类,则
∑ s ∈ S η ( s ) = p ∣ G ∣ \sum_{s\in S}\eta(s)=p|G| s∈S∑η(s)=p∣G∣故而等价类数目为
p = 1 ∣ G ∣ ∑ s ∈ S η ( s ) = 1 ∣ G ∣ ∑ π ∈ G ψ ( π ) p=\frac{1}{|G|}\sum_{s\in S}\eta(s)=\frac{1}{|G|}\sum_{\pi\in G}\psi(\pi) p=∣G∣1s∈S∑η(s)=∣G∣1π∈G∑ψ(π)证毕!
这篇关于伯恩赛德定理(集合S的 置换群 诱导出来的等价关系 对集合S 划分 得到的 等价类个数)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





