等价关系专题
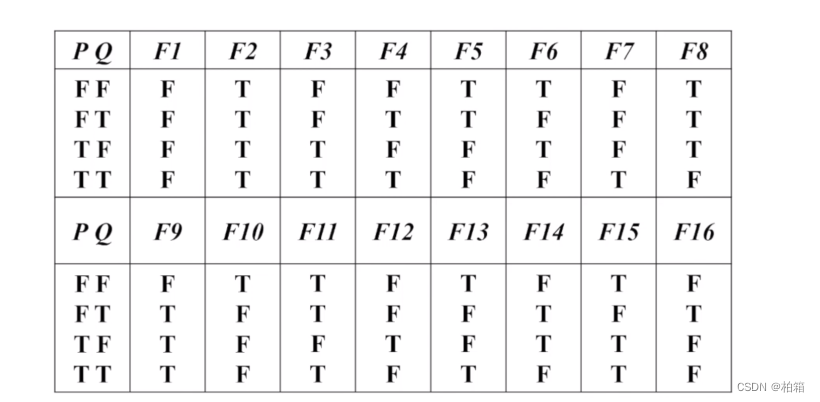
离散数学——(2)真值表,等价关系,等价置换定理,重言式与蕴含式,重言式与蕴含式,其他联结词,或非,其他联结词真值表
目录 1.真值表 1.真值表的构造编辑 2.真值表的性质 3.成真和成假指派 2.等价关系 1.基本等价关系 3.等价置换定理 4.重言式与蕴含式 1.可满足式 2.蕴含式 3.基本的蕴含式 5.其他联结词 1.异或 2.条件否定 3.与非 6.或非 7.其他联结词真值表 1.真值表 1.真值表的构造 2.真值表的性质
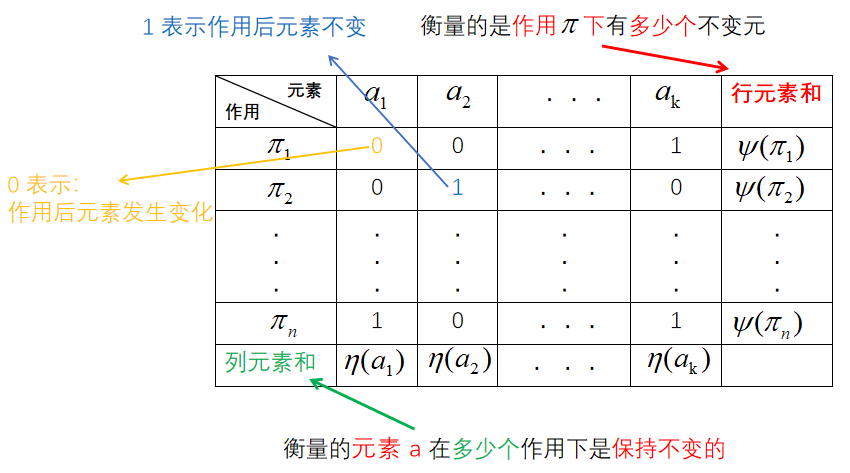
伯恩赛德定理(集合S的 置换群 诱导出来的等价关系 对集合S 划分 得到的 等价类个数)
前言:仅个人小记。这个定理就是用来计数的,用来数一数等价类的个数,而等价类本质上是一种降维表示,即把同种东西归类,进而达到简化的目的,进而更能凸现事物的本质。等价类的个数类似于线性代数里面 “秩” 这个概念,而不同的等价类则类似于不同的 “基向量” 。 前要知识和规定 1.由集合 S 上的一个置换群 < G , ∗ > <G,*> <G,∗>诱导的二元关系 R是一个等
基于模糊等价关系的模糊聚类分析
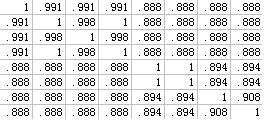
假设R是X上的模糊等价关系,则对任意的a,R的a-截集是X上的普通等价关系,因此,可以根据X上的模糊关系,对X进行模糊分类。当取不同的a值,则可以得到不同的分类结果,即分类是动态的。 实际操作中,一般情况下,我们所获得是一系列样本,假设有N个,每个样本可以看作是M维空间中的一个点。可以表示如下,论域: , 对第i个元素有 1.数据预处理
集合A(|A|=n)上可以定义多少种不同的等价关系
离散笔记 集合A(|A|=n)上可以定义多少种不同的等价关系?看个栗子再看一个例子一个直观的递归想法代入递归思想一般规律拓展思考 集合A(|A|=n)上可以定义多少种不同的等价关系? 一个包含n元素的集合A,有 2 n 2^{n} 2n个子集, A × A A \times A A×A笛卡尔积集合中有 n 2 n^2 n2个元素,对应的不同的二元关系(子集)有 2 n × n
【离散数学】——期末刷题题库(等价关系与划分)
🎃个人专栏: 🐬 算法设计与分析:算法设计与分析_IT闫的博客-CSDN博客 🐳Java基础:Java基础_IT闫的博客-CSDN博客 🐋c语言:c语言_IT闫的博客-CSDN博客 🐟MySQL:数据结构_IT闫的博客-CSDN博客 🐠数据结构:数据结构_IT闫的博客-CSDN博客 💎C++:C++_IT闫的博客-CSDN博客 🥽C51单片机:C51单片机(STC89
高数 | 【无穷级数】等价无穷小(Talor展开)判敛法 交错级数不能用通项等价关系审敛
一、引例 我们知道,对于正项级数可以利用所谓的通项等价关系进行审敛,即 废话不多说,看例题 : 二、经错标零 例题你觉得简单?下面这坑你必踩~ 经典的错误,标准的零分~ 关注A选项~ 你的做法: 应用性质:在级数中加上或减去有限项后级数的敛散性不变 设从某一项 N 之后, 运用等价无穷小 如果按照交错级数审敛法(莱布