基于模糊等价关系的模糊聚类分析

本文主要是介绍基于模糊等价关系的模糊聚类分析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

假设R是X上的模糊等价关系，则对任意的a,R的a-截集是X上的普通等价关系，因此，可以根据X上的模糊关系，对X进行模糊分类。当取不同的a值，则可以得到不同的分类结果，即分类是动态的。

实际操作中，一般情况下，我们所获得是一系列样本，假设有N个，每个样本可以看作是M维空间中的一个点。可以表示如下，论域：，对第i个元素有

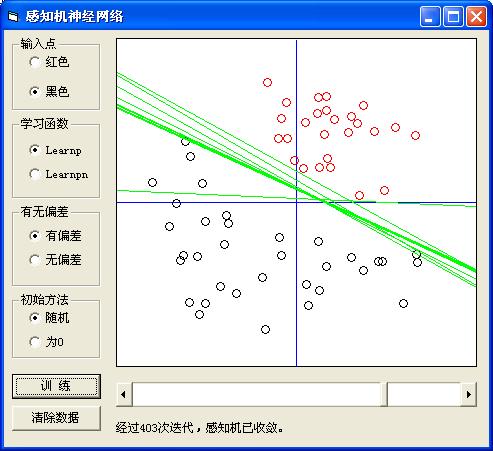
1.数据预处理

考虑到不同的数据可能有不同的量纲，因此，再处理之前，有必要对数据进行相当的变换。常用的变换标准差变换和极差变换：

标准差变换：

经过变换后，每个变量的均值为0，标准差为1，并可以消除量纲的影响，但值不一定在0和1之间。

极差变换：

经过变换后，消除了量纲的影响，并且值在0和1之间。

2 模糊相似矩阵的建立

由已知的数据，可以建立论域上的模糊关系矩阵，其目的是为构造模糊等价矩阵提供数据。

计算模糊关系矩阵由很多方法，如夹角余弦法，相关系数法，算术平均法，几何平均法，最大最小法，以夹角余弦为例，可用下述公式计算：

3 用传递闭包法求模糊等价矩阵

由以上过程所建立的矩阵一般仅具有自反性和对称性，不满度传递性，必须进行变换转换为模糊等价矩阵。常采用传递闭包法，即从上述R矩阵出发，求R^2-->R^4-->R^8...，直到第一次出现R^k × R^k＝R^k，这时表明R以具有传递性。

4 根据模糊等价矩阵和某以a得到分类结果。

部分代码实现：

'**********************************数据的标准差变化****************************
'
'过程名：   Norm_Diff
'参    数：   Data()   - Double ,待变换的二维数组
'说    明：   执行改函数后数组中了保存变换的数据
'作    者：
'修改者：   laviepbt
'修改日期：   2006-11-1
'
'**********************************数据的标准差变化****************************

Public Sub Norm_Diff(ByRef Data() As Double)
    Dim m As Integer, N As Integer, i As Integer, j As Integer
    Dim Ave As Double, s As Double
    N = UBound(Data, 1): m = UBound(Data, 2)      'n样品数，m变量数
    For j = 1 To m
        Ave = 0
        For i = 1 To N
            Ave = Ave + Data(i, j)
        Next
        Ave = Ave / N                       'ave是平均值
        s = 0
        For i = 1 To N
            s = s + (Data(i, j) - Ave) ^ 2     's是标准差
        Next
        s = Sqr(s / N)
        For i = 1 To N
            Data(i, j) = (Data(i, j) - Ave) / s
        Next
    Next
End Sub

'**********************************数据的极差变换****************************
'
'过程名：   Extre_Diff
'参    数：   Data()   - Double ,待变换的二维数组
'说    明：   执行改函数后数组中了保存变换的数据
'作    者：
'修改者：   laviepbt
'修改日期：   2006-11-1
'
'**********************************数据的极差变换****************************

Public Sub Extre_Diff(ByRef Data() As Double)
    Dim m As Integer, N As Integer, i As Integer, j As Integer
    Dim Max As Double, Min As Double, d As Double
    N = UBound(Data, 1): m = UBound(Data, 2)      'N样品数，M变量数
    For j = 1 To m
        Max = -10000000000#: Min = 10000000000#
        For i = 1 To N
            If Data(i, j) > Max Then Max = Data(i, j)
            If Data(i, j) < Min Then Min = Data(i, j)
        Next
        d = Max - Min                   'd是极差
        For i = 1 To N
            Data(i, j) = (Data(i, j) - Min) / d   '极差标准化变换
        Next
    Next
End Sub

'**********************************夹角余弦法****************************
'
'过程名：   Angle_Cos
'参    数：   Data() - Double ,二维数组数据
'             R() - Double, 相似矩阵
'说    明：
'作    者：
'修改者：   laviepbt
'修改日期：   2006-11-1
'
'**********************************夹角余弦法****************************

Public Sub Angle_Cos(ByRef Data() As Double, ByRef R() As Double)
    Dim m As Integer, N As Integer, i As Integer, j As Integer, k As Integer
    Dim S1 As Double, Si2 As Double, Sj2 As Double
    N = UBound(Data, 1): m = UBound(Data, 2)      'N样品数，M变量数
    For i = 1 To N
        For j = 1 To N
            If i = j Then
                R(i, j) = 1
            Else
                S1 = 0: Si2 = 0: Sj2 = 0
                For k = 1 To m
                    S1 = S1 + Data(i, k) * Data(j, k)
                    Si2 = Si2 + Data(i, k) ^ 2
                    Sj2 = Sj2 + Data(j, k) ^ 2
                Next
                R(i, j) = Int((S1 / Sqr(Si2 * Sj2)) * 1000 + 0.5) / 1000
            End If
        Next
    Next

End Sub

'**********************************相关系数法****************************
'
'过程名：   Correlation
'参    数：   Data() - Double ,二维数组数据
'             R() - Double, 相似矩阵
'说    明：
'作    者：
'修改者：   laviepbt
'修改日期：   2006-11-1
'
'**********************************相关系数法****************************

Public Sub Correlation(ByRef Data() As Double, ByRef R() As Double)
    Dim m As Integer, N As Integer, i As Integer, j As Integer, k As Integer
    Dim Xia As Double, Xja As Double
    Dim S1 As Double, Si2 As Double, Sj2 As Double
    N = UBound(Data, 1): m = UBound(Data, 2)      'N样品数，M变量数
    For i = 1 To N
        For j = 1 To N
            If i = j Then
                R(i, j) = 1
            Else
                Xia = 0: Xja = 0
                For k = 1 To m
                    Xia = Xia + Data(i, k)
                    Xja = Xja + Data(j, k)
                Next
                Xia = Xia / m
                Xja = Xja / m

                S1 = 0: Si2 = 0: Sj2 = 0
                For k = 1 To m
                    S1 = S1 + Abs((Data(i, k) - Xia) * (Data(j, k) - Xja))
                    Si2 = Si2 + (Data(i, k) - Xia) ^ 2
                    Sj2 = Sj2 + (Data(j, k) - Xja) ^ 2
                Next
                R(i, j) = Int((S1 / Sqr(Si2 * Sj2)) * 1000 + 0.5) / 1000
            End If
        Next
    Next
End Sub

'**********************************传递闭包法****************************
'
'过程名：   TR
'参    数：   R() - Double ,相似矩阵
'             RR() - Double, 模糊乘积矩阵
'说    明：
'作    者：
'修改者：   laviepbt
'修改日期：   2006-11-1
'
'**********************************传递闭包法****************************

Public Sub TR(ByRef R() As Double, ByRef RR() As Double)
    Dim N As Integer, l As Integer
    Dim i As Integer, j As Integer, k As Integer
    Dim i1 As Integer, j1 As Integer
    Dim dMax As Double
    N = UBound(R, 1)
    ReDim dMin(1 To N) As Double
    l = 0
100:
    l = l + 1
    If l > 100 Then
        MsgBox "已进行100次自乘，仍然没有获得传递性", vbCritical, "错误"
        Exit Sub
    End If
    For i = 1 To N
        For j = 1 To N
            For k = 1 To N
                If R(i, k) <= R(k, j) Then
                    dMin(k) = R(i, k)
                Else
                    dMin(k) = R(k, j)
                End If
            Next
            dMax = dMin(1)              '模糊矩阵的乘法，取小取大
            For k = 1 To N
                If dMin(k) > dMax Then dMax = dMin(k)
            Next
            RR(i, j) = dMax
        Next
    Next
    For i = 1 To N
        For j = 1 To N
            '判断是否式模糊等价矩阵，若非则继续做
            If R(i, j) <> RR(i, j) Then
                For i1 = 1 To N
                    For j1 = 1 To N
                        R(i1, j1) = RR(i1, j1)
                    Next
                Next
                GoTo 100
            End If
        Next
    Next
End Sub

全部代码可参考《模糊数学基础及实用算法》一书。

处理结果：以一下数据为例：选用极差法预处理数据，夹角余弦法计算相似矩阵

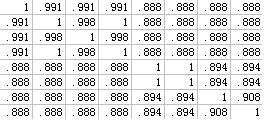
数据模糊等价矩阵

部分分析结果：

********************************
入值:0.908
第1类:U1 U2 U3 U4
第2类:U5 U6
第3类:U7 U8
F效验值: 6.099
显著性为.2的临界值：2.259
显著性为.1的临界值：3.78
结论：在给定的临界值下，该分类效果特别显著.^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
********************************
入值:0.894
第1类:U1 U2 U3 U4
第2类:U5 U6 U7 U8
F效验值: 7.634
显著性为.2的临界值：2.073
显著性为.1的临界值：3.776
结论：在给定的临界值下，该分类效果特别显著.^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
********************************
入值:0.888
第1类:U1 U2 U3 U4 U5 U6 U7 U8
F效验值: ********
显著性为.2的临界值：********
显著性为.1的临界值：********
结论：在给定的临界值下，该分类效果不显著.
********************************