D. Valera and Swaps time limit per test 1 second memory limit per test 256 megabytes input standard input output standard output A permutation p of length n is a sequence of distinc

poj1721  题意：给出一个由n个数组成的经过m次置换（即把a[i]=a[a[i]]）后的群，求原来的那个群。  找出循环节  -----  直接模拟！！   如 案列：n=7,m=4;     6 3 1 2 4 7 5                       一次变化 7 1 6 3 2 5 4                       二次变化 4 7 5 6 1 2 3

题目链接： http://poj.org/problem?id=3128 题目大意： 给你一行共 26 个字母，代表一个置换。问：这个置换能否为某个置换平方的结果。 解题思路： 这道题可参考《置换群快速幂运算研究与探讨》，里边有详解。这里放上结论。 结论一： 一个长度为 l 的循环 T，l 是 k 的倍数，则 T^k 是 k 个循环的乘积，每个 循环分别是循环 T 中下

题意：有一个序列，你需要将通过交换使得序列最后单调增。每次交换的代价为交换的两个数的和，求将序列变成单调增地最小代价 和。 思路：如果有一个序列：8 4 5 3 2 7 ，那么最终的序列为：2 3 4 5 7 8 。如果视作是一个置换群的作用，那么可以写出循环之积： （8 2 7）（4 3 5）。对于每个循环，每个数都至少被交换一次，所以我们应该用循环中的最小值和每个数交换，设循环数的最小值

UVA 12103 - Leonardo's Notebook 题目链接 题意：给定一个字母置换B，求是否存在A使得A^2=B 思路：任意一个长为 L 的置换的k次幂，会把自己分裂成gcd(L,k) 分， 并且每一份的长度都为 L / gcd(l,k)，因此平方对于奇数长度不变，偶数则会分裂成两份长度相同的循环，因此如果B中偶数长度的循环个数不为偶数必然不存在A了 代码：

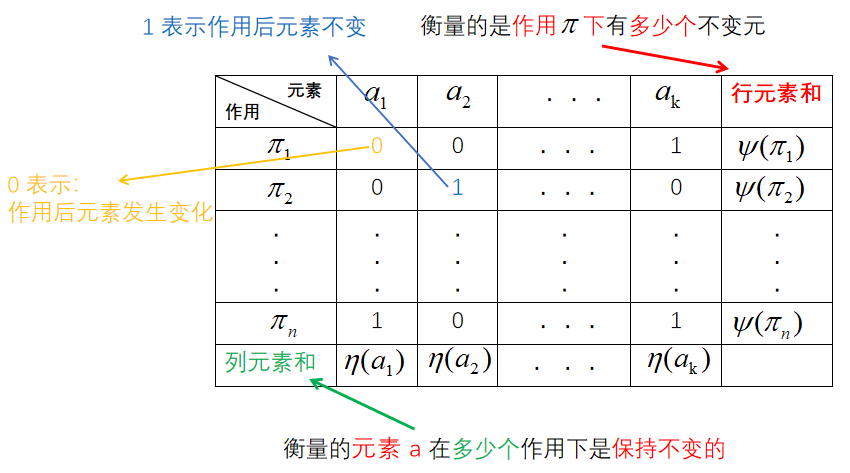
前言：仅个人小记。这个定理就是用来计数的，用来数一数等价类的个数，而等价类本质上是一种降维表示，即把同种东西归类，进而达到简化的目的，进而更能凸现事物的本质。等价类的个数类似于线性代数里面 “秩” 这个概念，而不同的等价类则类似于不同的 “基向量” 。 前要知识和规定 1.由集合 S 上的一个置换群 &lt; G , ∗ &gt; &lt;G,*&gt; <G,∗>诱导的二元关系 R是一个等

点击转到 1.   4,1,5,2,3->2,4,3,1,5->1,2,5,4,3->4,1,3,2,5->2,4,5,1,3->1,2,3,4,5->4,1,5,2,3 　　要经过6次映射能变回4,1,5,2,3（循环节的最小公倍数） #include<iostream>#include<cstdio> #include<algorithm>using namespace std;

题目 给出一个置换，写出该置换的轮换表示。比如 表示为(1 3 6 7 8 4 2)(5 9) 输入： 置换后的序列 输出： 不相杂的轮换乘积，每行表示一个轮换（轮换的起始数字最小，每个轮换的起始数字递增排序，单轮换省略） 例如： 样例1： 输入：（空格分隔） 3 1 6 2 9 7 8 4 5 输出： 1 3 6 7 8 4 2（空格分隔） 5 9（空格分隔） 样

相关群的概念： 对称群（symmetric group），设X是一个集合（可以是无限集），X上的一个双射：a:X→X（即是置换）。集合X上的所有置换构成的族记为S(x)，S(x)关于映射的复合运算构成了一个群，当X是有限集时，设X中的元素个数为n，则称群S(x)为n次对称群。 将S(x)的子群统称为变换群（transformation group）。 置换群 一类具体的有限群。有限集合到自