《零基础实践深度学习》基于线性回归实现波士顿房价预测任务1.3.3

本文主要是介绍《零基础实践深度学习》基于线性回归实现波士顿房价预测任务1.3.3，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1.3.3 基于线性回归实现波士顿房价预测任务

深度学习不仅实现了模型的端到端学习，还推动了人工智能进入工业大生产阶段，产生了标准化、自动化和模块化的通用框架。不同场景的深度学习模型具备一定的通用性，五个步骤即可完成模型的构建和训练，如图3所示。

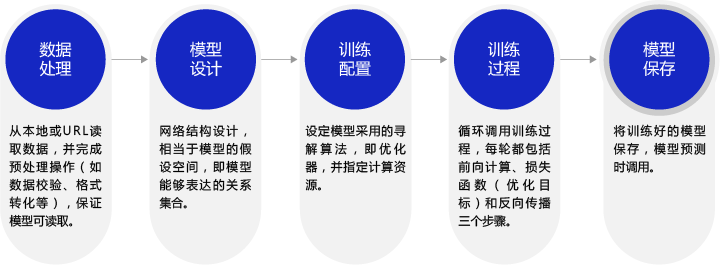
图3：构建神经网络/深度学习模型的基本步骤

正是由于深度学习的建模和训练的过程存在通用性，即在构建不同的模型时，只有模型三要素不同，其它步骤基本一致，才产生了深度学习框架来加速建模。

1.3.3.1 数据处理

数据处理包含五个部分：数据导入、数据形状变换、数据集划分、数据归一化处理和封装load data函数。数据预处理后，才能被模型调用。

说明：

本教程中的代码都可以在AI Studio上直接运行，Print结果都是基于程序真实运行的结果。
由于是真实案例，代码之间存在依赖关系，因此需要读者逐条、全部运行，否则会导致命令执行报错。

（1）数据读取

通过如下代码读入数据，了解下波士顿房价的数据集结构，数据存放在本地目录下housing.data文件中。

In [1]

# 导入需要用到的package
import numpy as np
import json
# 读入训练数据
datafile = './work/housing.data'
data = np.fromfile(datafile, sep=' ')
data

array([6.320e-03, 1.800e+01, 2.310e+00, ..., 3.969e+02, 7.880e+00,1.190e+01])

（2）数据形状变换

由于读入的原始数据是1维的，所有数据都连在一起。因此需要我们将数据的形状进行变换，形成一个2维的矩阵，每行为一个数据样本（14个值），每个数据样本包含13个x（影响房价的特征）和一个y（该类型房屋的均价）。

In [2]

# 读入之后的数据被转化成1维array，其中array的第0-13项是第一条数据，第14-27项是第二条数据，以此类推.... 
# 这里对原始数据做reshape，变成N x 14的形式
feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE','DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]
feature_num = len(feature_names)
data = data.reshape([data.shape[0] // feature_num, feature_num])

In [3]

# 查看数据
x = data[0]
print(x.shape)
print(x)

(14,)

[6.320e-03 1.800e+01 2.310e+00 0.000e+00 5.380e-01 6.575e+00 6.520e+01 4.090e+00 1.000e+00 2.960e+02 1.530e+01 3.969e+02 4.980e+00 2.400e+01]

（3）数据集划分

将数据集划分成训练集和测试集，其中训练集用于确定模型的参数，测试集用于评判模型的效果。为什么要对数据集进行拆分，而不能直接应用于模型训练呢？这与学生时代的授课和考试关系比较类似，如图4所示。

图4：训练集和测试集拆分的意义

上学时总有同学，平时不认真学习，将习题死记硬背下来，但是成绩往往并不好。因为学校期望学生掌握的是知识，而不仅仅是习题本身。另出新的考题，才能鼓励学生努力去掌握习题背后的原理。同样我们期望模型学习的是任务的本质规律，而不是训练数据本身，模型训练未使用的数据，才能更真实的评估模型的效果。

在本案例中，我们将80%的数据用作训练集，20%用作测试集，实现代码如下。通过打印训练集的形状，可以发现共有404个样本，每个样本含有13个特征和1个预测值。

In [4]

ratio = 0.8
offset = int(data.shape[0] * ratio)
training_data = data[:offset]
training_data.shape

(404, 14)

（4）数据归一化处理

对每个特征进行归一化处理，使得每个特征的取值缩放到0~1之间。这样做有两个好处：一是模型训练更高效；二是特征前的权重大小可以代表该变量对预测结果的贡献度（因为每个特征值本身的范围相同）。

In [5]

# 计算train数据集的最大值，最小值
maximums, minimums = \training_data.max(axis=0), \training_data.min(axis=0), 
# 对数据进行归一化处理
for i in range(feature_num):data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])

使得前面的系数更有意义

（5）封装成load data函数

将上述几个数据处理操作封装成load data函数，以便下一步模型的调用，实现方法如下。

In [6]

def load_data():# 从文件导入数据datafile = './work/housing.data'data = np.fromfile(datafile, sep=' ')# 每条数据包括14项，其中前面13项是影响因素，第14项是相应的房屋价格中位数feature_names = [ 'CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', \'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV' ]feature_num = len(feature_names)# 将原始数据进行Reshape，变成[N, 14]这样的形状data = data.reshape([data.shape[0] // feature_num, feature_num])# 将原数据集拆分成训练集和测试集# 这里使用80%的数据做训练，20%的数据做测试# 测试集和训练集必须是没有交集的ratio = 0.8offset = int(data.shape[0] * ratio)training_data = data[:offset]# 计算训练集的最大值，最小值maximums, minimums = training_data.max(axis=0), \training_data.min(axis=0)# 对数据进行归一化处理for i in range(feature_num):data[:, i] = (data[:, i] - minimums[i]) / (maximums[i] - minimums[i])# 训练集和测试集的划分比例training_data = data[:offset]test_data = data[offset:]return training_data, test_data

In [7]

# 获取数据
training_data, test_data = load_data()
x = training_data[:, :-1]
y = training_data[:, -1:]

In [8]

# 查看数据
print(x[0])
print(y[0])

[0. 0.18 0.07344184 0. 0.31481481 0.57750527

0.64160659 0.26920314 0. 0.22755741 0.28723404 1.

0.08967991]

[0.42222222]

1.3.3.2 模型设计

模型设计是深度学习模型关键要素之一，也称为网络结构设计，相当于模型的假设空间，即实现模型“前向计算”（从输入到输出）的过程。

如果将输入特征和输出预测值均以向量表示，输入特征x有13个向量，y有1个向量，那么参数权重的形状是13×1。假设我们以如下任意数字赋值参数做初始化：

w=[0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, -0.1, -0.2, -0.3, -0.4, 0.0]

In [9]

w = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, -0.1, -0.2, -0.3, -0.4, 0.0]
w = np.array(w).reshape([13, 1])

取出第1条样本数据，观察样本的特征向量与参数向量相乘的结果。

In [10]

x1=x[0]
t = np.dot(x1, w)
print(t)

[0.69474855]

完整的线性回归公式，还需要初始化偏移量b，同样随意赋初值-0.2。那么，线性回归模型的完整输出是z=t+b，这个从特征和参数计算输出值的过程称为“前向计算”。

In [11]

b = -0.2
z = t + b
print(z)

[0.49474855]

将上述计算预测输出的过程以“类和对象”的方式来描述，类成员变量有参数w和b。通过写一个forward函数（代表“前向计算”）完成上述从特征和参数到输出预测值的计算过程，代码实现如下。

In [12]

class Network(object):def __init__(self, num_of_weights):# 随机产生w的初始值# 为了保持程序每次运行结果的一致性，# 此处设置固定的随机数种子np.random.seed(0)self.w = np.random.randn(num_of_weights, 1)self.b = 0.def forward(self, x):z = np.dot(x, self.w) + self.breturn z

基于Network类的定义，模型的计算过程如下所示。

In [13]

net = Network(13)
x1 = x[0]
y1 = y[0]
z = net.forward(x1)
print(z)

[2.39362982]

1.3.3.3 训练配置（模型的损失与优化）

模型设计完成后，需要通过训练配置寻找模型的最优值，即通过损失函数来衡量模型的好坏。训练配置也是深度学习模型关键要素之一。

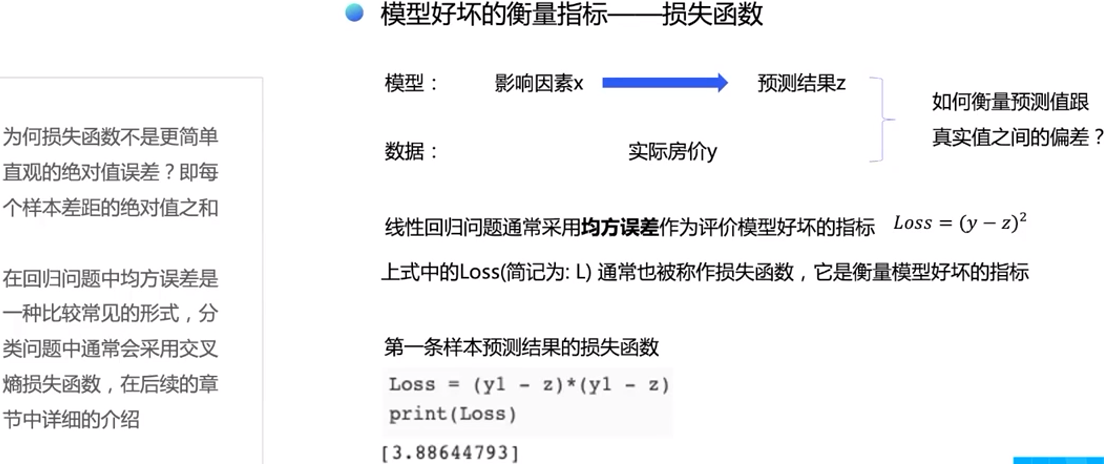
通过模型计算x1表示的影响因素所对应的房价应该是z, 但实际数据告诉我们房价是y。这时我们需要有某种指标来衡量预测值z跟真实房价值y之间的差距。对于回归问题，最常采用的衡量方法是使用均方误差作为评价模型好坏的指标，公式为

Loss=(y−z)^2

上式中的Loss通常也被称作损失函数，它是衡量模型好坏的指标。在回归问题中常用均方误差作为损失函数，而在分类问题中常用采用交叉熵（Cross-Entropy）作为损失函数，在后续的章节中会更详细的介绍。对其中任意一个样本计算损失函数值的代码实现如下：

选取损失函数的合理性：

1. 比较现实的物理含义；
2. 最好在整个优化的过程中，是比较好求解和优化的

In [14]

Loss = (y1 - z)*(y1 - z)
print(Loss)

[3.88644793]

因为计算损失函数时需要把每个样本的损失函数值都考虑到，所以我们需要对单个样本的损失函数进行求和，并除以样本总数N。公式为

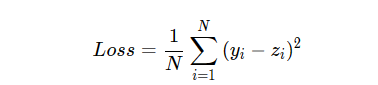
在Network类下面添加损失函数的代码实现如下：

In [15]

class Network(object):def __init__(self, num_of_weights):# 随机产生w的初始值# 为了保持程序每次运行结果的一致性，此处设置固定的随机数种子np.random.seed(0)self.w = np.random.randn(num_of_weights, 1)self.b = 0.def forward(self, x):z = np.dot(x, self.w) + self.breturn zdef loss(self, z, y):error = z - ycost = error * errorcost = np.mean(cost)return cost

使用定义的Network类，可以方便的计算预测值和损失函数。需要注意的是，类中的变量x,w，b,z,error等均是向量。以变量x为例，共有两个维度，一个代表特征数量（值为13），一个代表样本数量，代码如下所示。

In [16]

net = Network(13)
# 此处可以一次性计算多个样本的预测值和损失函数
x1 = x[0:3]
y1 = y[0:3]
z = net.forward(x1)
print('predict: ', z)
loss = net.loss(z, y1)
print('loss:', loss)

predict: [[2.39362982]

[2.46752393]

[2.02483479]]

loss: 3.384496992612791

这篇关于《零基础实践深度学习》基于线性回归实现波士顿房价预测任务1.3.3的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！