Acwing---838. 堆排序

2024-02-11 14:52

文章标签 堆排序 acwing 838

本文主要是介绍Acwing---838. 堆排序，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

堆排序

1.题目
2.基本思想
3.代码实现

1.题目

输入一个长度为 n的整数数列，从小到大输出前 m 小的数。

输入格式
输入一个长度为 n 的整数数列，从小到大输出前 m 小的数。

输出格式
共一行，包含 m 个整数，表示整数数列中前 m 小的数。

数据范围
$1≤m≤n≤10^5，$

$1≤数列中元素≤10^9$

输入样例：

5 3
4 5 1 3 2

输出样例：

1 2 3

2.基本思想

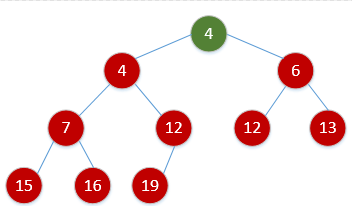
如何手写一个堆？完全二叉树 5个操作

插入一个数 heap[ ++ size] = x; up(size);
求集合中的最小值 heap[1]
删除最小值 heap[1] = heap[size]; size -- ;down(1);
删除任意一个元素 heap[k] = heap[size]; size -- ;up(k); down(k);
修改任意一个元素 heap[k] = x; up(k); down(k);

3.代码实现

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Scanner;public class Main {static int N = 100010;static int[] h = new int[N];static int size;public static void main(String[] args) throws IOException {Scanner sc = new Scanner(System.in);int n = sc.nextInt(), m = sc.nextInt();for (int i = 1; i <= n; i++) h[i] = sc.nextInt();size = n;//初始化size,表示堆里有n 个元素for (int i = n / 2; i > 0; i--) down(i);//把堆初始化成小根堆，从二叉树的倒数第二行开始，把数字大的下沉while (m-- > 0) {System.out.print(h[1] + " ");//小顶堆 最小就是第一个h[1] = h[size];//末尾元素上移size--;down(1);}}private static void down(int u) {int min = u;//存储三个结点中存在的最小的结点的下标，初始化为当前结点minif (u * 2 <= size && h[u * 2] < h[min]) min = u * 2;//左子节点存在并且小于当前结点，更新min的下标if (u * 2 + 1 <= size && h[u * 2 + 1] < h[min]) min = u * 2 + 1;//右子节点存在并且小于当前结点，更新min的下标if (min != u) {//如果min==u意味着不用变动，u就是三个结点中拥有最小值的结点下标，否则交换数值int temp = h[min];h[min] = h[u];h[u] = temp;down(min);//交换数值后，min这个结点存储原本u的值，u存储存储min的值（三个数中的最小值）。u不用调整了，但min情况不明，可能需要调整。直到它比左右子节点都小}}
}