本文主要是介绍代码随想录算法训练营第四十七天(动态规划篇)| 416. 分割等和子集,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
416. 分割等和子集
题目链接:416. 分割等和子集 - 力扣(LeetCode)
思路
回溯——超时
首先想到之前的回溯算法,寻找数组中加和等于sum(nums)/2的子集,但对于大数组超时了:
class Solution(object):def backtracking(self, nums, startIdx, curSum):if curSum > sum(nums)/2:return if curSum == sum(nums)/2 and sum(nums)%2 == 0:return Truefor i in range(startIdx, len(nums)):curSum += nums[i]if self.backtracking(nums, i+1, curSum) == True:return TruecurSum -= nums[i]return Falsedef canPartition(self, nums):return self.backtracking(nums, 0, 0)动态规划
可以把数组中的每个元素看作一个物体,那么寻找符合要求的子集相当于把将所选的物体装入一定容量的背包。根据之前的学习,我们知道如何求定容背包能装的最大价值,如果把每一个元素的数值同时当成该物体的重量和价值,就可以用01背包求解。
如果容量为sum/2的背包能装的最大价值为sum/2(即可以被装满),则说明这个数组可以被分割成两个子集。
e,g, 对于数组[1, 2, 5], 有三个物体,它们的重量和价值分别为1,2,5,那对于容量为sum/2 = 4的背包,最多只能装1+2 = 3的价值,说明不能被分割。
1. dp数组定义
容量为j的背包,所背的物品价值最大可以为dp[j]。
若dp[j] == j 说明集合中的某子集总和正好可以凑成总和j;如果dp[sum/2] = sum/2,说明数组可以被分割成等和子集。
2. dp递推公式
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题,相当于背包里放入物品i的重量是nums[i],其价值也是nums[i]。
所以递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
3. 初始条件
当背包的容量为0时,能装的最大价值为0,所以dp[0]=0。如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,如果题目给的价值有负数,那么非0下标就要初始化为负无穷。
4. 遍历顺序
根据01背包的滚动数组的方法:
代码随想录算法训练营第四十六天(动态规划篇)|01背包(滚动数组方法)-CSDN博客
如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包容量的for循环放在内层,且内层for循环倒序遍历!
5. 举例推导dp数组
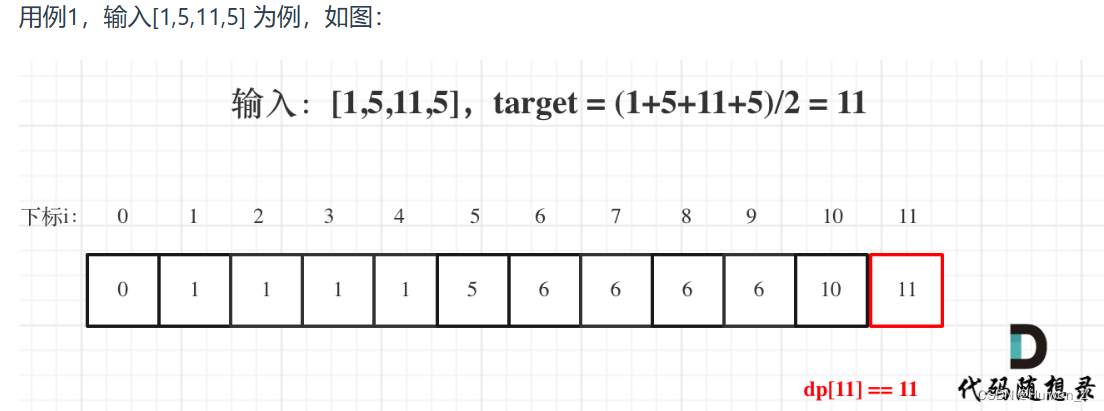
代码实现
class Solution(object):def canPartition(self, nums): # 剪枝:如果数组总和为奇数,则不能分割成等和子集if sum(nums)%2 == 1:return Falsetarget = sum(nums)/2dp = [0] * (target + 1)for num in nums:for j in range(target, num-1, -1): # 等于省略了之前if的条件之前的题需要trace weight[i]的值dp[j] = max(dp[j], dp[j-num] + num)return dp[target] == target
需要注意,在循环背包容量时,我们用
for j in range(target, num-1, -1):因为对于重量(价值)为num的物体只能放在容量大于他自身重量的包里。这一个条件在之前的01背包代码是由下面的if语句实现:
if weight[i] > j:dp[j] = dp[j]如果当前重量大于背包容量,就选择不装物品i,这相当于不考虑背包容量小于当前物体的值,即不在for循环中遍历。事实上之前的代码:
for i in range(objNum): # 遍历物体for j in range(bagWeight, 0, -1): #遍历背包容量if weight[i] > j:dp[j] = dp[j]else:dp[j] = max(dp[j], dp[j - weight[i]] + value[i])也可以改为:
for i in range(objNum): # 遍历物体for j in range(bagWeight, weight[i] - 1, -1): # 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i])这篇关于代码随想录算法训练营第四十七天(动态规划篇)| 416. 分割等和子集的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





