本文主要是介绍高级数据结构与算法 | 布谷鸟过滤器(Cuckoo Filter):原理、实现、LSM Tree 优化,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- Cuckoo Filter
- 基本介绍
- 布隆过滤器
- 局限
- 变体
- 布谷鸟哈希
- 布谷鸟过滤器
- 实现
- 数据结构
- 优化项
- Victim Cache
- 备用位置计算
- 半排序桶
- 插入
- 查找
- 删除
- 应用场景:LSM 优化
Cuckoo Filter
基本介绍
如果对布隆过滤器不太了解,可以看看往期博客:海量数据处理(一) :位图与布隆过滤器的概念以及实现
布隆过滤器
局限
对于需要处理海量数据的时候,如果我们需要快速判断一条记录是否,通常会使用过滤器来进行验证,而其中最常见的就是布隆过滤器(Bloom Filter)——其通过多个哈希函数,将同一个字符串映射到多个位置上,查询时一旦有任何一个位置为零,即可快速的判断出文件不存在。
基于以上特点,布隆过滤器存在一个严重问题,即假阳性。基于哈希的方式容易出现哈希碰撞,这就会导致某些数据可能不存在,但是其对应的位置已经被标记为 1。且由于布隆过滤器不支持删除(会导致其他元素被误删),随着过滤器中元素的增加,误报率也会指数级增加。
因此布隆过滤器通常会用于元素数量可预测的场景,否则一旦元素数量过多,就需要重建过滤器并 rehash。
变体
在海量数据处理的场景中,我们往往无法预测数据的规模,而重建过滤器的开销又过大,因此需要一个支持删除元素的过滤器,根据不同的实现方法,衍生出了以下变体:
- 计数布隆过滤器(Counting Bloom Filter):不再使用位来标记元素,而是使用一个计数器,删除一个元素时即将对应位置的计数减一,当计数为零时代表元素不存在。该方法虽然支持了删除,但是空间随着计数器大小成倍增加。
- 阻塞布隆过滤器(Blocked Bloom Filter):多层级的布隆过滤器(类似 CPU 的多级缓存),将集合分为多个布隆过滤器(每个过滤器相互独立,哈希函数也不同),首先决定哈希到哪个布隆过滤器,再在对应的布隆过滤器中使用对应的哈希函数进行插入。该方法的空间利用率高且假阳率低,但是实现较为复杂,且需要手动调整块大小和哈希函数,否则会因为某个小布隆过滤器负载不均导致假阳率增加。
- 动态左计数布隆过滤器(d-Left Counting Bloom Filter):该方法结合了上述两种方法的思想,将集合分为多个小布隆过滤器,并且每个块中的每一个位置都维护一个计数器。该方法比起计数布隆过滤器,空间利用率更高,但是在分布式场景下合并计数器的开销也会严重增加。
- 商过滤器(Quotient Filter):该方法将集合划分为多个桶,每个桶中保存一个元素和一个余数。首先对元素哈希得到一个整数值,整数值的高位为桶的下标,低位代表余数,通过对比对应下标的余数是否相同来判断元素存在。该方法的缺点在于需要使用额外的元数据来管理每个元素,并且桶数需要为 2 的幂次方。
在所有的变体中,应用最为广泛,效果最好的就是布谷鸟过滤器(Cuckoo Filter)。
布谷鸟哈希
在介绍布谷鸟过滤器之前,首先就要介绍其核心原理——布谷鸟哈希算法。
布谷鸟不会自己筑巢,下蛋后会将自己的蛋放入别的鸟类巢穴中,由其他鸟代为抚育,而幼鸟则会将其他未出生的鸟蛋推出鸟巢,自己独享食物。
布谷鸟哈希的原理就来源于上面的故事,他的核心在于哈希替换——布谷鸟哈希中每一个元素中有两个桶,分别使用了两种哈希函数存储两个下标,其中一个是主位置,另一个则是备用的位置。当主位置发生哈希冲突时,就会将元素存储到备用位置中,而如果备用位置也产生了冲突,就会将原有冲突的元素剔除,让其重复执行之前的流程,直到次数达到阈值时,才认为哈希表已满,进行 rehash。
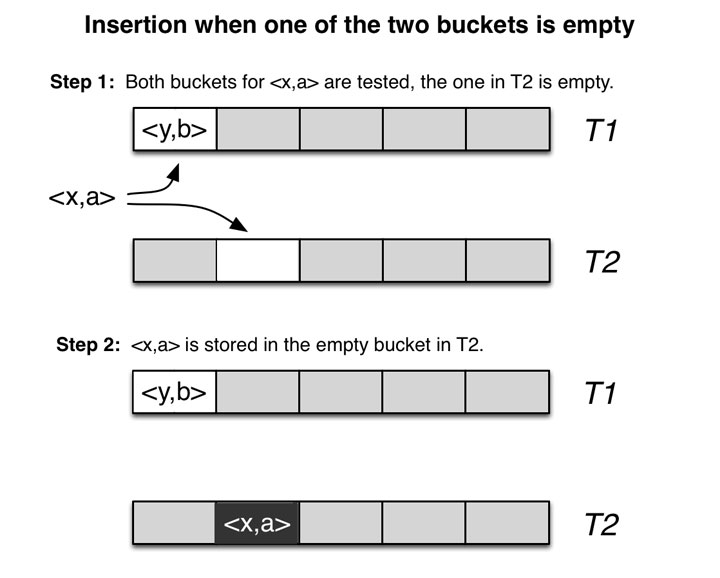
如上图,当 <x,a> 插入时,由于主位置已经存储有了 <y,b>,此时则将其插入到另一个表的备用位置中。
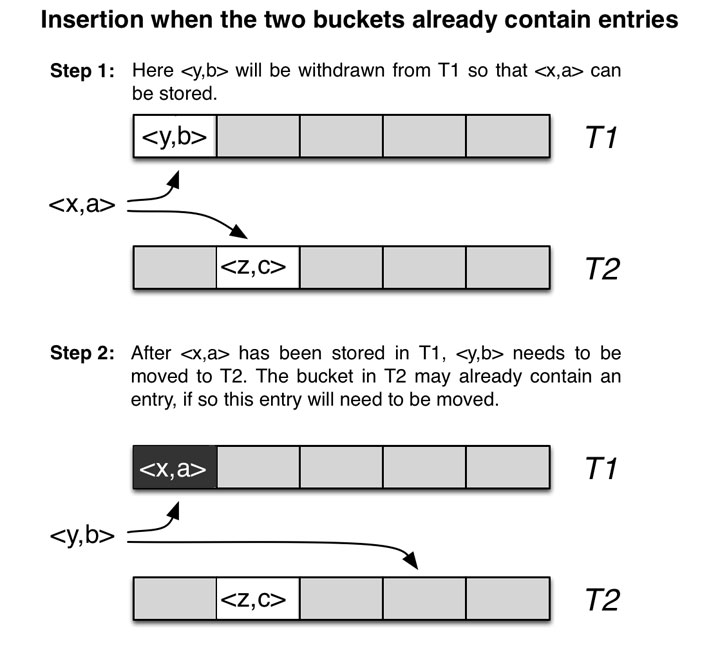
如上图,如果在插入时主位置和备用位置都被占用了,此时就会将主位置的 <y,b> 踢出来,将 <x,a> 插入进去,而 <y,b> 则需要去寻找其自己的备用位置进行插入。
删除的实现也非常简单,只需要将对应位置的元素给抹去即可。
布谷鸟过滤器
这里简单介绍核心思路,详细原理可以阅读论文 Cuckoo Filter: Practically Better Than Bloom
为了提高空间利用率,降低碰撞概率,布谷鸟过滤器在布谷鸟哈希上做了改进,将其从一维的结构变成了二维的结构(每个桶存储的元素从一个变为 n 个),且每个位置中只存储几个 bit 的指纹,而非完整的元素。
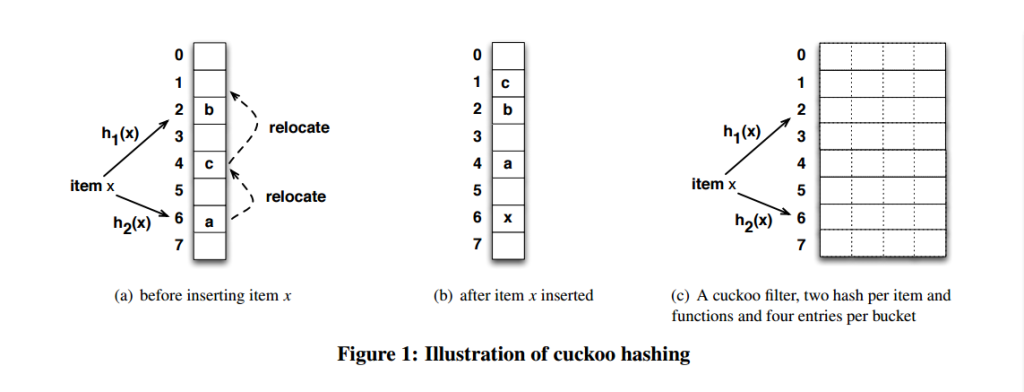
如上图,每个桶中存储了 4 个 slot,只有当一个桶中的所有 slot 都被填满的时候,才会使用替换的策略。这里的桶结构使用了一个二维数组来表示。
实现
这里以论文作者的源代码来分析如何实现一个布谷鸟过滤器,代码仓库:https://github.com/efficient/cuckoofilter
数据结构
// A cuckoo filter class exposes a Bloomier filter interface,
// providing methods of Add, Delete, Contain. It takes three
// template parameters:
// ItemType: the type of item you want to insert
// bits_per_item: how many bits each item is hashed into
// TableType: the storage of table, SingleTable by default, and
// PackedTable to enable semi-sorting
template <typename ItemType, size_t bits_per_item,template <size_t> class TableType = SingleTable,typename HashFamily = TwoIndependentMultiplyShift>
class CuckooFilter {// 底层存储元素的表TableType<bits_per_item> *table_;// 用于统计当前元素数量的计数器size_t num_items_;// 淘汰缓存VictimCache victim_;// 哈希函数族HashFamily hasher_;// 根据哈希值计算出indexinline size_t IndexHash(uint32_t hv) const;// 根据哈希值计算出taginline uint32_t TagHash(uint32_t hv) const;// 将上面两个函数抽象,对一个元素计算出index和taginline void GenerateIndexTagHash(const ItemType& item, size_t* index,uint32_t* tag) const;// 计算出元素的备用位置inline size_t AltIndex(const size_t index, const uint32_t tag) const;// 插入的实现逻辑Status AddImpl(const size_t i, const uint32_t tag);// 计算当前的负载因子double LoadFactor() const { return 1.0 * Size() / table_->SizeInTags(); }// 计算出当前过滤器每个元素占用的大小。随着该值升高,空间利用率、假阳率逐渐降低。double BitsPerItem() const { return 8.0 * table_->SizeInBytes() / Size(); }public:explicit CuckooFilter(const size_t max_num_keys) : num_items_(0), victim_(), hasher_();~CuckooFilter() { delete table_; }// 添加一个元素.Status Add(const ItemType &item);// 查找元素是否存在Status Contain(const ItemType &item) const;// 从过滤器中删除一个元素Status Delete(const ItemType &item);// 用于输出一些统计信息std::string Info() const;// 获取当前过滤器中元素数量size_t Size() const { return num_items_; }// 获取当前过滤器总大小size_t SizeInBytes() const { return table_->SizeInBytes(); }
};
优化项
Victim Cache
typedef struct {size_t index;uint32_t tag;bool used;
} VictimCache;
除了上面介绍中提到的内容,作者在这里还用到了一个小型的缓存 Victim Cache,用于存储在插入过程中被置换出去,但又无法被重新插入到其他位置的元素。通过这样一个单元素的 Cache 就可以提升插入成功率,并降低失败导致的 rehash 的开销。
备用位置计算
在 AltIndex 函数中,作者通过两个小技巧对 CuckooFilter 进行了优化。
inline size_t AltIndex(const size_t index, const uint32_t tag) const {return IndexHash((uint32_t)(index ^ (tag * 0x5bd1e995)));
}
- 异或计算:通过将主 index 和 tag 进行异或计算,得到备 index 的值。这样做的好处是,可以只存储一个 index 和一个 tag,通过将任意一个 index 和 tag 进行异或则可以得到另一个 index 的值。(三个值中的任意两个值进行异或计算,都可以得出第三个值)
- 负载均衡:从上面的代码可以看到,在进行异或计算之前,这里对 tag 还进行了乘法处理,这里使用了 0x5bd1e995,它是一个常用的乘法因子(如 MurmurHash),用于帮助哈希函数具有更好的分布,降低冲突。接着对异或完的结果再次进行一次哈希,这样可以尽可能的确保两个桶的位置随机且独立,达到负载均衡的目的。
半排序桶
除了默认的 SingleTable,作者还基于半排序桶对 tag 进行压缩,实现了 PackedTable 用于优化空间。
这里简单介绍下原理,详细实现可参考:https://github.com/efficient/cuckoofilter/blob/master/src/packedtable.h
其核心思路为将每个桶中的 tag 进行压缩。假设当前每个桶有 2 个 slot,每个 tag 用 4 bit 来表示(实际按 8 bit,即 1byte 分配)。在未进行压缩时,每个桶需要 16 bit 存储 tag 信息。假设数据为 1011 和 1000,此时可以简单的将数据组合为 10111000,此时只需要 8 bit 即可存储数据。
由于 PackedTable 中有大量位计算,为了方便讲解,这里以默认的 SingleTable 为例,分析关键步骤——插入、查找、删除。
插入
template <typename ItemType, size_t bits_per_item,template <size_t> class TableType, typename HashFamily>
Status CuckooFilter<ItemType, bits_per_item, TableType, HashFamily>::Add(const ItemType &item) {size_t i;uint32_t tag;if (victim_.used) {return NotEnoughSpace;}GenerateIndexTagHash(item, &i, &tag);return AddImpl(i, tag);
}template <typename ItemType, size_t bits_per_item,template <size_t> class TableType, typename HashFamily>
Status CuckooFilter<ItemType, bits_per_item, TableType, HashFamily>::AddImpl(const size_t i, const uint32_t tag) {size_t curindex = i;uint32_t curtag = tag;uint32_t oldtag;for (uint32_t count = 0; count < kMaxCuckooCount; count++) {bool kickout = count > 0;oldtag = 0;if (table_->InsertTagToBucket(curindex, curtag, kickout, oldtag)) {num_items_++;return Ok;}if (kickout) {curtag = oldtag;}curindex = AltIndex(curindex, curtag);}victim_.index = curindex;victim_.tag = curtag;victim_.used = true;return Ok;
}inline bool SingleTable::InsertTagToBucket(const size_t i, const uint32_t tag,const bool kickout, uint32_t &oldtag) {for (size_t j = 0; j < kTagsPerBucket; j++) {if (ReadTag(i, j) == 0) {WriteTag(i, j, tag);return true;}}if (kickout) {size_t r = rand() % kTagsPerBucket;oldtag = ReadTag(i, r);WriteTag(i, r, tag);}return false;
}
插入的执行流程如下:
- 计算出
tag、i。 - 判断
victim_是否被使用,如果被使用则认为当前表已满,无法插入,直接返回失败,否则继续。 - 此时开始尝试将元素插入到主位置中,如果插入成功则直接返回。
- 如果插入失败,此时会尝试将元素插入到备用位置,并将备用位置的元素踢出,尝试将备用元素插入到它自己的备用位置。
- 重复 3 ~ 4 的过程,直到达到最大上限
kMaxCuckooCount。此时认为表已满,将被踢出的元素存入victim_。
查找
template <typename ItemType, size_t bits_per_item,template <size_t> class TableType, typename HashFamily>
Status CuckooFilter<ItemType, bits_per_item, TableType, HashFamily>::Contain(const ItemType &key) const {bool found = false;size_t i1, i2;uint32_t tag;GenerateIndexTagHash(key, &i1, &tag);i2 = AltIndex(i1, tag);assert(i1 == AltIndex(i2, tag));found = victim_.used && (tag == victim_.tag) &&(i1 == victim_.index || i2 == victim_.index);if (found || table_->FindTagInBuckets(i1, i2, tag)) {return Ok;} else {return NotFound;}
}
查找的执行流程如下:
- 计算出
tag、i1、i2。 - 查找元素是否在
victim_,如果查找成功则直接返回。 - 查找元素是否存在表中,如果存在则返回成功,否则失败。
inline bool SingleTable::FindTagInBuckets(const size_t i1, const size_t i2,const uint32_t tag) const {const char *p1 = buckets_[i1].bits_;const char *p2 = buckets_[i2].bits_;uint64_t v1 = *((uint64_t *)p1);uint64_t v2 = *((uint64_t *)p2);// caution: unaligned access & assuming little endianif (bits_per_tag == 4 && kTagsPerBucket == 4) {return hasvalue4(v1, tag) || hasvalue4(v2, tag);} else if (bits_per_tag == 8 && kTagsPerBucket == 4) {return hasvalue8(v1, tag) || hasvalue8(v2, tag);} else if (bits_per_tag == 12 && kTagsPerBucket == 4) {return hasvalue12(v1, tag) || hasvalue12(v2, tag);} else if (bits_per_tag == 16 && kTagsPerBucket == 4) {return hasvalue16(v1, tag) || hasvalue16(v2, tag);} else {for (size_t j = 0; j < kTagsPerBucket; j++) {if ((ReadTag(i1, j) == tag) || (ReadTag(i2, j) == tag)) {return true;}}return false;}
}
- 这里会根据元素位数和桶中 slot 的数量,选择不同的查找方式,查找 tag 是否存储于桶中。当主位置不存在时,则会查找备位置。
- 当有任何一个位置存在元素时,认为查找成功
删除
template <typename ItemType, size_t bits_per_item,template <size_t> class TableType, typename HashFamily>
Status CuckooFilter<ItemType, bits_per_item, TableType, HashFamily>::Delete(const ItemType &key) {size_t i1, i2;uint32_t tag;GenerateIndexTagHash(key, &i1, &tag);i2 = AltIndex(i1, tag);if (table_->DeleteTagFromBucket(i1, tag)) {num_items_--;goto TryEliminateVictim;} else if (table_->DeleteTagFromBucket(i2, tag)) {num_items_--;goto TryEliminateVictim;} else if (victim_.used && tag == victim_.tag &&(i1 == victim_.index || i2 == victim_.index)) {// num_items_--;victim_.used = false;return Ok;} else {return NotFound;}
TryEliminateVictim:if (victim_.used) {victim_.used = false;size_t i = victim_.index;uint32_t tag = victim_.tag;AddImpl(i, tag);}return Ok;
}inline bool DeleteTagFromBucket(const size_t i, const uint32_t tag) {for (size_t j = 0; j < kTagsPerBucket; j++) {if (ReadTag(i, j) == tag) {assert(FindTagInBucket(i, tag) == true);WriteTag(i, j, 0);return true;}}return false;
}
查找的执行流程如下:
- 计算出
tag、i1、i2。 - 分别尝试从桶的
i1、i2位置删除数据。如果成功删除,则当前表中有新空间,此时将victim_中的元素存入表中,并将其标记为空。 - 查找元素是否在
victim_,如果是则直接将其清空,如果不存在则认为当前不存在该数据,返回失败。
应用场景:LSM 优化
相比较于布隆过滤器,布谷鸟过滤器主要有以下优缺点:
- 优点
- 支持动态添加/删除元素。
- 高负载因子场景下,其查找性能更高。
- 如果目标要求假阳性率低于 3%,则它更能节省空间。
- 实现更加简单。
- 缺点
- 当表过满时,插入操作可能失败。
- 相同元素的哈希值可能不同,在极端场景下,插入重复元素可能会不断触发
rehash直到上限。(可以通过在插入前先判断是否存在,但又会导致性能降低) - 与上一条同理,如果同一元素插入多次,则需要循环删除直到失败,否则无法保证数据完全清除。
布谷鸟过滤器有什么比较典型的用例吗?
- 为什么大部分NOSQL数据库选择使用LSM树而非B+树?
- LevelDB 源码剖析(五)SSTable模块:SSTable、Block、布隆过滤器、LRU Cache
在我之前的博客中曾经介绍过 LSM Tree,这是目前较为流行的一种磁盘存储结构。
在传统的实现方法中,为了避免不必要的磁盘 I/O,通常都会使用布隆过滤器用以加速查询。由于布隆过滤器无法删除,为防止数据随着 Merge 不断膨胀,导致过滤器效果降低,LSM 通常会对每层 SSTable 都生成一个。
这样不仅造成了读放大,还导致大量的空间浪费。因此可以通过使用布谷鸟过滤器来对 LSM 进行优化:
详细原理可参考论文:Chucky: A Succinct Cuckoo Filter for LSM-Tree
- 维护一个全局的布谷鸟过滤器,当过滤器查询不存在时则直接返回查询失败。
- 布谷鸟过滤器中记录了 Key => Fingerprints + Level ID 的映射。Fingerprints 用于避免冲突,Level ID 用于定位数据位于哪一个 Level。

查询、更新复杂度
如上图:
- 查询:通过 Key 计算出指纹,并找到所有过滤器中指纹相同的条目,按照 Level 由低到高查找数据。
- 以上图为例,在桶中查询 k7,此时两个桶中分别有两个条目与其指纹 Y 相匹配。此时优先查找层数较低(代表新数据)的 Level 4,发现误判,接着查询 Level 5 时成功。
- 插入:当数据从内存的
Memtable写入SStable时,不需要考虑过滤器中的已有条目。- 以上图为例,直接写入 x,1 而不考虑原有的 x,2(为防止重复数据大量写入导致溢出,论文中有提到拓展桶机制,这里不过多介绍)。
- 当 LSM 进行
Merge时,再更新 Level ID 并删除重复数据。

通过引入布谷鸟过滤器,可以大幅度提高 LSM 的性能。
这篇关于高级数据结构与算法 | 布谷鸟过滤器(Cuckoo Filter):原理、实现、LSM Tree 优化的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






