本文主要是介绍基于BatchNorm的模型剪枝【详解+代码】,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 1、BatchNorm(BN)
- 2、L1与L2正则化
- 2.1 L1与L2的导数及其应用
- 2.2 论文核心点
- 3、模型剪枝的流程
- ICCV经典论文,通俗易懂!论文题目:Learning Efficient Convolutional Networks through Network Slimming
- 卷积后能得到多个特征图,这些图一定都重要吗?
- 训练模型的时候能否加入一些策略,让权重参数体现出主次之分?
- 以上这两点就是论文的核心,先看论文再看源码其实并不难!
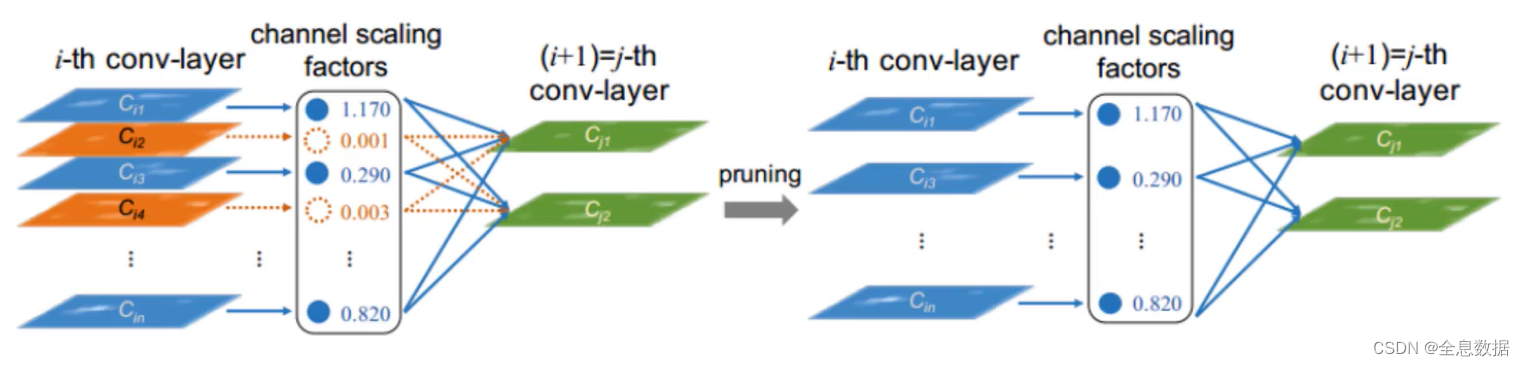
如下图所示,每个conv-layer会被计算相应的channel scaling factors,然后根据channel scaling factors筛选conv-layer,达到模型瘦身的作用,图中的1.170,0.001,0.290等就是下面我们将要介绍的学习参数 γ \gamma γ 值,
1、BatchNorm(BN)
Network slimming,就是利用BN层中的缩放因子 γ \gamma γ,
整体感觉就是一个归一化操作,但是BN中还额外引入了两个可训练的参数: γ \gamma γ和 β \beta β。
BN的公式:
x ^ ( k ) = γ ⋅ x ( k ) − E [ x ( k ) ] V a r [ x ( k ) ] + β \hat x^{(k)}=\gamma \cdot \frac{x^{(k)}-E[x^{(k)}]}{\sqrt{Var[x^{(k)}]}}+\beta x^(k)=γ⋅Var[x(k)]x(k)−E[x(k)]+β
- 如果训练时候输入数据的分布总是改变,网络模型还能学的好吗?
- 不能,网络刚开始学起来会很差,而且还容易导致过拟合,
- 对于卷积层来说,它的输入可不是只有原始输入数据
- 而是卷积层+BN层+relu层输出的数据,如果输入只来自卷积层,那么数据不在同一个分布内,网络刚开始学起来会很差,而且还容易导致过拟合
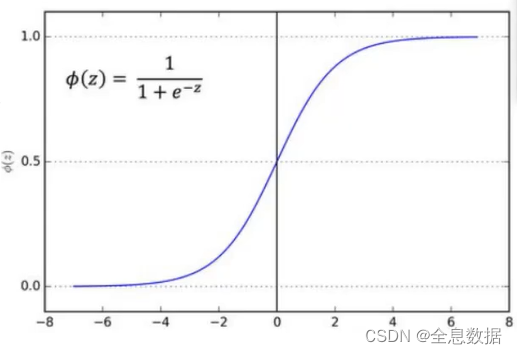
- 以sigmoid为例,如果不经过BN层,很多输出值越来也偏离,导致模型收敛越来越难!
A、BN的作用
- BN要做的就是把越来越偏离的分布给他拉回来!
- 再重新规范化到均值为0方差为1的标准正态分布
- 这样能够使得激活函数在数值层面更敏感,训练更快
- 有一种感觉:经过BN后,把数值分布强制分布在了非线性函数的线性区域中,而图像本身是非线性的,所以这是一个缺陷,所以就引入了 γ \gamma γ 参数,
B、BatchNorm参数
- 如果都是线性的了,神经网络还有意义吗?
- BN另一方面还需要保证一些非线性,对规范化后的结果再进行变换
- 这两个参数是训练得到的: y ( k ) = γ x ^ ( k ) + β ( k ) y^{(k)} = \gamma \hat x^{(k)} + \beta ^{(k)} y(k)=γx^(k)+β(k)
- 感觉就是从正态分布进行一些改变,拉动一下,变一下形状!
图中的1.170,0.001,0.290等就是学习参数 γ \gamma γ 值, γ \gamma γ 值越大则说明该特征层越重要,越小则不重要,

2、L1与L2正则化
如果学习到的 γ \gamma γ 值是1.17,1.16,1.15等,那如何筛选比较重要的 γ \gamma γ 值呢?使用L1正则化就可以实现筛选比较重要的 γ \gamma γ 值,
- 论文中提出:训练时使用L1正则化能对参数进行稀疏作用,
- L1:对权重参数稀疏与特征选择,会对一些权重参数稀疏化接近于0,
- L2:平滑特征,会对权重参数都接近于0,
L1正则化: J ( θ → ) = 1 2 ∑ i = 1 m ( h θ ~ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n ∣ θ j ∣ J\big(\overrightarrow{\theta}\big)= \frac{1}{2}\sum_{i=1}^m\big(h_{\widetilde{\theta}}(x^{(i)})-y^{(i)}\big)^2+\lambda \sum_{j=1}^n|\theta_j| J(θ)=21∑i=1m(hθ (x(i))−y(i))2+λ∑j=1n∣θj∣
L2正则化: J ( θ → ) = 1 2 ∑ i = 1 m ( h θ ~ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 J\big(\overrightarrow{\theta}\big)= \frac{1}{2}\sum_{i=1}^m\big(h_{\widetilde{\theta}}(x^{(i)})-y^{(i)}\big)^2+\lambda \sum_{j=1}^n\theta_j^2 J(θ)=21∑i=1m(hθ (x(i))−y(i))2+λ∑j=1nθj2
其中 h θ ~ ( x ( i ) ) h_{\widetilde{\theta}}(x^{(i)}) hθ (x(i))是预测值, y ( i ) y^{(i)} y(i)是标签值,
2.1 L1与L2的导数及其应用
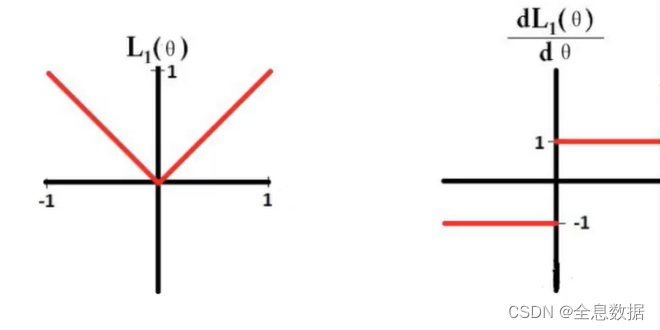
L1的导数:
L1求导后为:sign( θ \theta θ),相当于稳定前进,都为 ± 1 \pm 1 ±1;所以迭代次数够多,有些特征层权重 θ \theta θ 最后可以学成0了,所以L1可以做稀疏化,
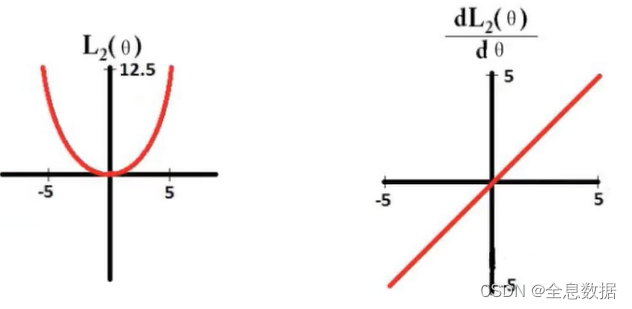
L2的导数:
L2求导为:θ,梯度下降过程越来越慢,相应的权重参数都接近0,起到平滑的作用,
2.2 论文核心点
以BN中的 γ \gamma γ 为切入点,即 γ \gamma γ 越小,其对应的特征图越不重要,
为了使得 γ \gamma γ 能有特征选择的作用,引入L1正则来控制 γ \gamma γ ,
L = ∑ ( x , y ) l ( f ( x , W ) , y ) + λ ∑ γ ∈ Γ g ( γ ) L=\sum_{(x,y)}l\big(f(x,W),y\big)+\lambda\sum_{\gamma \in \Gamma}g(\gamma) L=(x,y)∑l(f(x,W),y)+λγ∈Γ∑g(γ)
其中 l ( f ( x , W ) , y ) l\big(f(x,W),y\big) l(f(x,W),y)是loss损失函数, γ \gamma γ 是BN中的参数 γ \gamma γ,
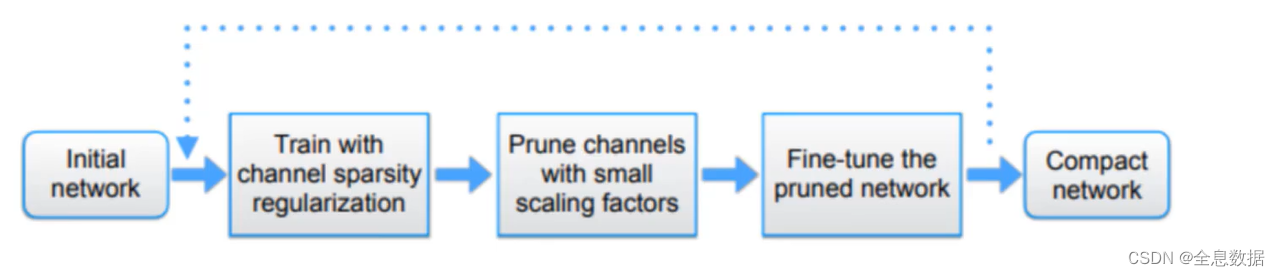
3、模型剪枝的流程
训练-剪枝-再训练,整体流程如下图所示,
这篇关于基于BatchNorm的模型剪枝【详解+代码】的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!