机器学习入门（3）——多变量线性回归(Linear Regression with Multiple Variables)

本文主要是介绍机器学习入门（3）——多变量线性回归(Linear Regression with Multiple Variables)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

多维特征（Multiple Features）

多变量梯度下降（Gradient Descent for Multiple Variables）

与单变量线性回归类似，在多变量线性回归中，我们也构建一个代价函数，则这个代价函数是所有建模误差的平方和，即：
$$J\left({\theta }_0,{\theta }_1\dots {\theta }_n\right)=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2$$
其中：$$h_{\theta }(x)={\theta }^{T}X={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\dots +{\theta }_n{x}_n$$
我们的目标和单变量线性回归问题中一样，是要找出使得代价函数最小的一系列参数。

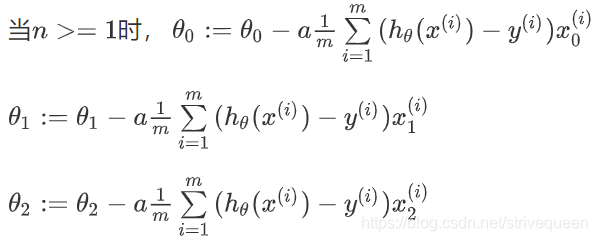
我们开始随机选择一系列的参数值，计算所有的预测结果后，再给所有的参数一个新的值，如此循环直到收敛。
代码示例：
计算代价函数
$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m{\left(h_{\theta }\left(x^{(i)}\right)-y^{(i)}\right)}^2$$
其中：$$h_{\theta }(x)={\theta }^{T}X={\theta }_0{x}_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\dots +{\theta }_n{x}_n$$
Python 代码：

def computeCost(X, y, theta):inner = np.power(((X * theta.T) - y), 2)return np.sum(inner) / (2 * len(X))

梯度下降法实践1-特征缩放（Feature Scaling）

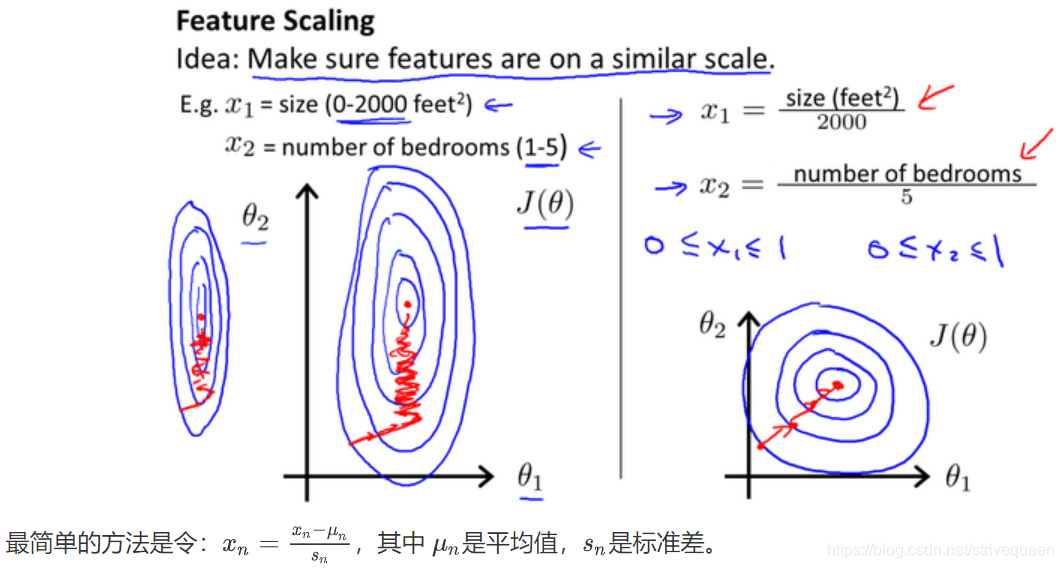
特征缩放：面对多维特征问题的时候，我们要保证这些特征都具有相近的尺度，这将帮助梯度下降算法更快地收敛，收敛所需的迭代次数更少。

梯度下降法实践2-学习率（Learning Rate）

梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，我们不能提前预知，我们可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。

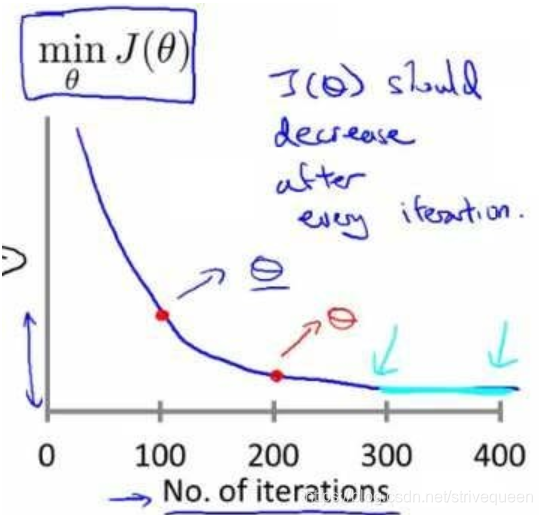
梯度下降算法的每次迭代受到学习率的影响，如果学习率α过小，则达到收敛所需的迭代次数会非常高；如果学习率α过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。
通常可以考虑尝试以下学习率：
α = 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, 3, 10

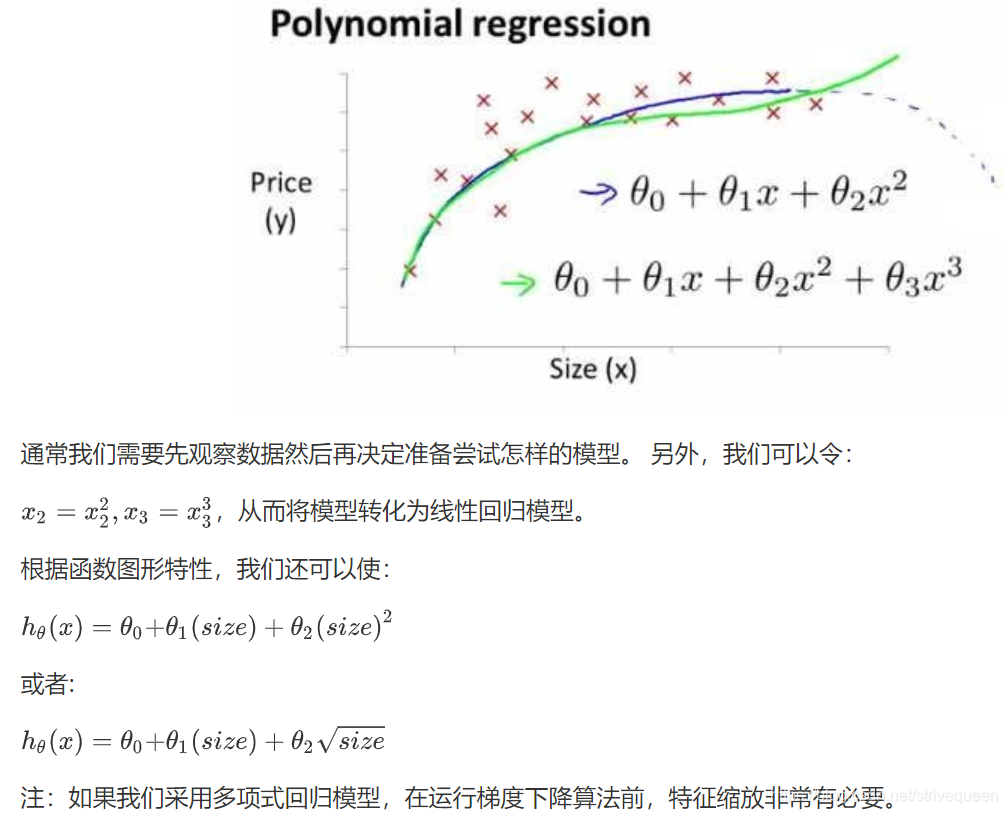
特征和多项式回归（Features and Polynomial Regression）

正规方程（Normal Equation）

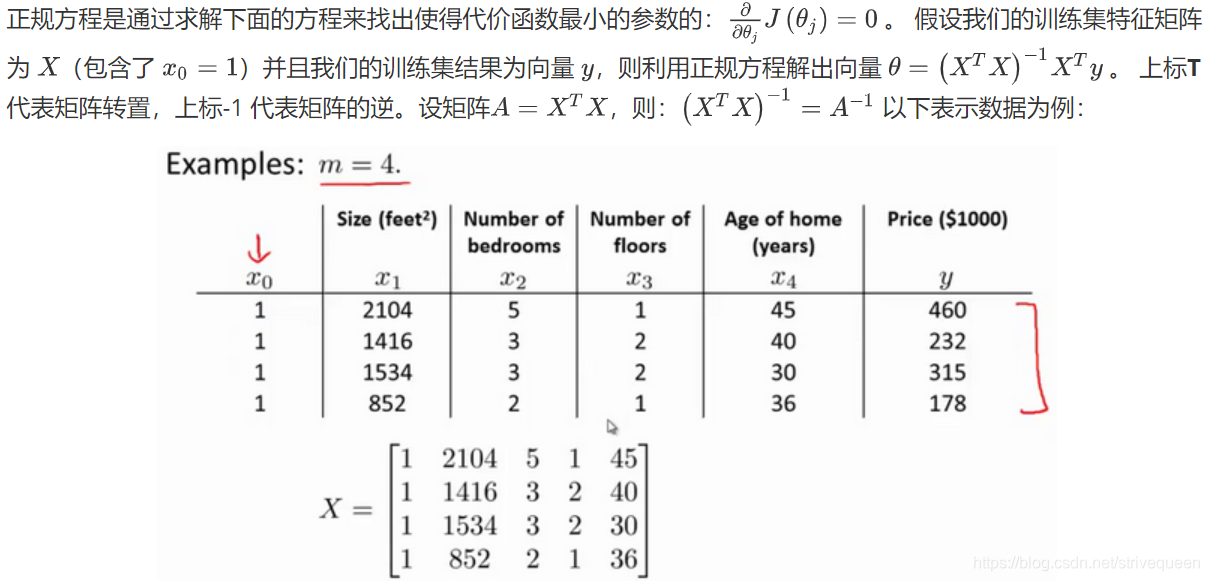
用正规方程方法求解参数：

注：对于那些不可逆的矩阵（通常是因为特征之间不独立，如同时包含英尺为单位的尺寸和米为单位的尺寸两个特征，也有可能是特征数量大于训练集的数量），正规方程方法是不能用的。
梯度下降与正规方程的比较：

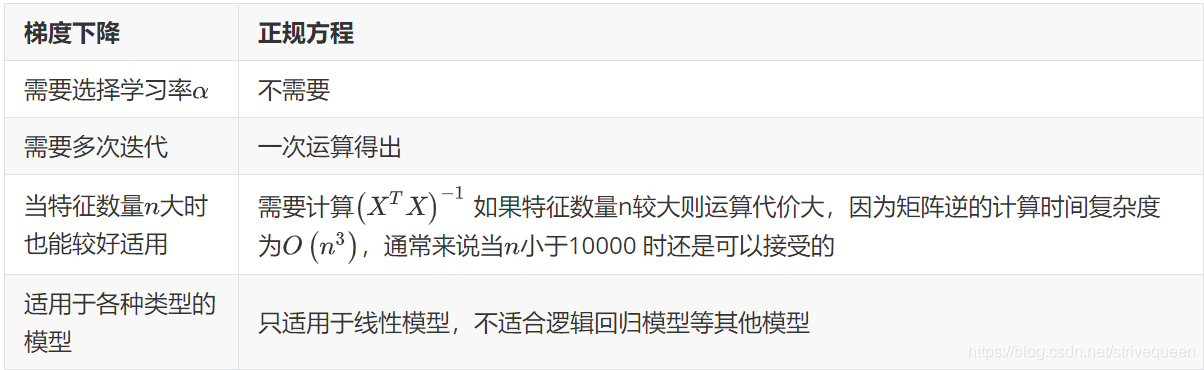
正规方程的python实现：

import numpy as npdef normalEqn(X, y):theta = np.linalg.inv(X.T@X)@X.T@y #X.T@X等价于X.T.dot(X)return theta

这篇关于机器学习入门（3）——多变量线性回归(Linear Regression with Multiple Variables)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---