8正交向量与子空间

本文主要是介绍8正交向量与子空间，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

前面还是图和网络的内容，感觉与自己所求相差较多，可以参考：https://blog.csdn.net/huang1024rui/article/details/68951624

第十四课时：正交向量与子空间

本文讲解什么是向量的正交，什么是子空间的正交，什么是基的正交。

正交向量

在n维空间中，向量之间的夹角是90度

判断两个向量 $X,Y$ 是否正交，求乘积 $X^TY$ 是否等于0，即如果 $X^TY=0$ ，则X,Y正交。

零向量与任何向量都正交。

正交子空间

如果子空间S与子空间T正交，那么S中的每个向量都和T中的每个向量正交。

如果两个子空间正交，那么他们必定不会交与某个非零向量。

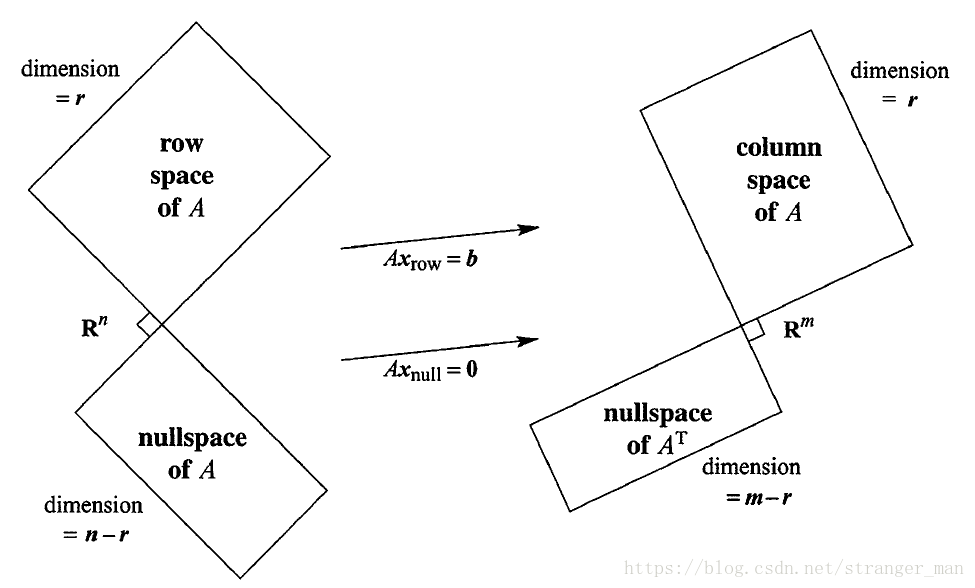
行空间和零空间是将整个n维空间一分为二的两个相互正交的子空间，两个子空间的维数和为n，称为n维空间里面的正交补（行空间的正交补包含与之正交的零空间的所有向量）。

若 $Ax=0$ 存在零空间，则零空间的向量与A的乘Ax=0，则表示A的各行乘以x向量得到零向量，说明A的行向量与x是正交的，但是是否A的行空间(行空间包含矩阵中的行向量以及这些行向量的线性组合)里所有的向量都与x正交呢？很明显x正交于行向量的线性组合。

列空间和左零空间是将整个m维空间一分为二的两个相互正交的子空间，两个子空间的维数和为m，称为m维空间里面的正交补。

以三维空间为例，n=3，矩阵A如果行空间是一维的一条直线，r=1，那么dimN(A)=2，零空间就是垂直于这条直线的一个平面。实际上向量（1 2 5）是这个平面的法向量。

可以把线性代数的内容分为几个部分：

1）第一部分是线性代数的基本定理，表明四个基本子空间之间的关系，重点是研究维数；
2）第二部分的重点是在已知维数的情况下研究它们的正交性；
3）第三部分是关于它们的基，即正交基。

如何求Ax=b 一个无解的方程组的解，即当Ax=b无解时（b不在A的列空间），如何去解这个方程组。

对于长方矩阵（很多情况下是无解的，因为b很可能不能由A的列向量线性组合得到），有时候A的方程很多，未知数很少，这时候有些方程可能得到的结果是有很大误差的，即坏数据，即b中有一部分是坏数据，其实求出方程的解只需要一小部分方程就够了，需要做的是把这些”坏数据“筛选出来，这是线性代数需要解决的问题，如何去求这个解，最优解是什么。

用代数的语言来描述这个问题：我们得到一些方程（这些方程无解），如何求出它们的最优解？一种方法是不断去掉一些方程，直到剩下一个可逆的方阵，然后求出它的解。但这种方法不好判断。

更好的方法是：矩阵 $A$ 是 $m×n$ 的长方矩阵，那么 $A^TA$ 结果就是一个 $n×n$ 的对称方阵。因此，当 $Ax=b$ 这是一个坏方程时，只需要把坏方程两侧乘以A转置，就得到好方程。