[论文阅读笔记21]Quo Vadis: Is Trajectory Forecasting the Key Towards Long-Term Multi-Object Tracking?

这篇文章是少有的根据轨迹预测来做MOT的文章.

论文链接: https://arxiv.org/pdf/2210.07681.pdf
代码: https://github.com/dendorferpatrick/QuoVadis

1. Abstract

长时跟踪是一个经常被忽略的问题. 对于大于三秒钟的轨迹丢失, SOTA的跟踪器中只能恢复不到10%的轨迹. 轨迹丢失的时间越长, 其搜索空间(也就是之后可能的位置)就越大, 因此本文用轨迹预测的方式减少丢失轨迹的搜索空间, 提高精度.

2. Introduction

作者认为, 仅仅依靠Re-ID特征来解决长时跟踪问题是不够的. 为此, 用轨迹预测的方式来减少lost轨迹可行的轨迹空间的搜索范围. 总的来说, 本文的贡献如下:

1. 研究了如何将单目多目标跟踪和轨迹预测两个领域结合起来研究
2. 研究了如何将MOT数据集在3D的birds-eye-view(BEV)的视角下定位目标
3. 在3D的BEV视角下通过求解轨迹预测来解决MOT的遮挡问题

3. Method

我们不能直接将轨迹预测应用到MOT上. 这是因为轨迹预测的数据集都是BEV视角, 而单目MOT的视角与相机的位置, 角度, 方向等等因素影响. 因此我们必须构造一个转换, 即将当前相机视角下的目标位置$p$映射到2D BEV下的位置$x$, 这中间需要计算一个单应矩阵$H$, 即有$x\propto Hp$.

所以, 我们通过估计单应矩阵将相机视角坐标映射到3D真实物理坐标, 随后利用一个在线的tracker将轨迹在真实物理坐标中定位, 随后利用轨迹预测对lost的轨迹进行估计, 再整合预测的结果.

3.1 数据驱动的单应矩阵估计

所谓数据驱动, 就是利用深度网络进行. 作者用一个深度估计网络估计画面的深度, 再利用一个语义分割网络来分割出画面中的"地面", 随后将分割出的"地面"映射到3D世界的xy平面, 也就是得到了单应矩阵$H$, 然后, 将目标bbox与地面的交界点映射到3D视角的xy平面, 就可以得到2D BEV视角的坐标了, 如下图所示:

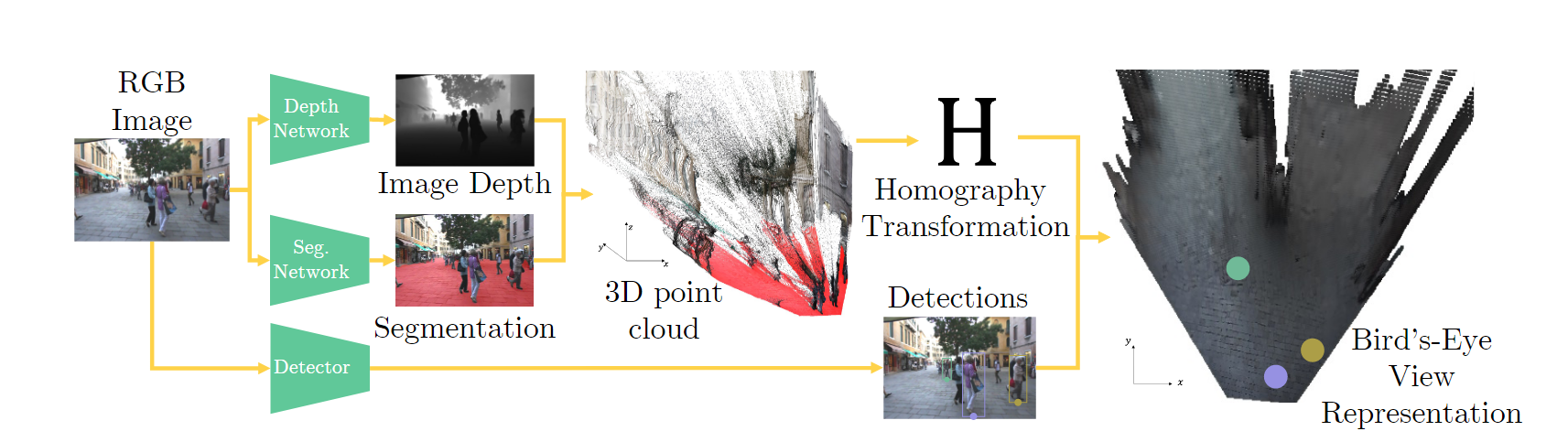
对于静止相机, 我们利用第一帧的信息得到的$H$即可.

对于运动相机, 每一帧都计算一个$H^t$, 之后通过光流计算平移向量.

3.2 预测

预处理:

简单来说, 就是将同一ID的轨迹映射在BEV坐标下, 为了防止噪声(BEV估计网络的噪声)的影响, 用Kalman滤波进行平滑. 此外, 轨迹预测网络要求轨迹的长度是恒定的, 因此当长度不够的时候, 利用线性外推的方式补充缺失的过去的轨迹.

轨迹预测的设计模式

简单来说, 作者利用了多个Social-GAN来预测轨迹.

3.3 通过预测进行跟踪

这一块说了很多, 实际上没啥, 就是对于lost的轨迹, 沿着轨迹预测网络得到的未来轨迹走, 以便将来和某个detection匹配. 匹配的原则就是iou, 欧氏距离和相似度, 如下式:

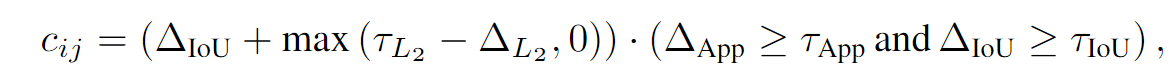
此外, 设置最大轨迹寿命, 要不然就匹配错了. 这也是很常规的做法.

3.4 整体流程

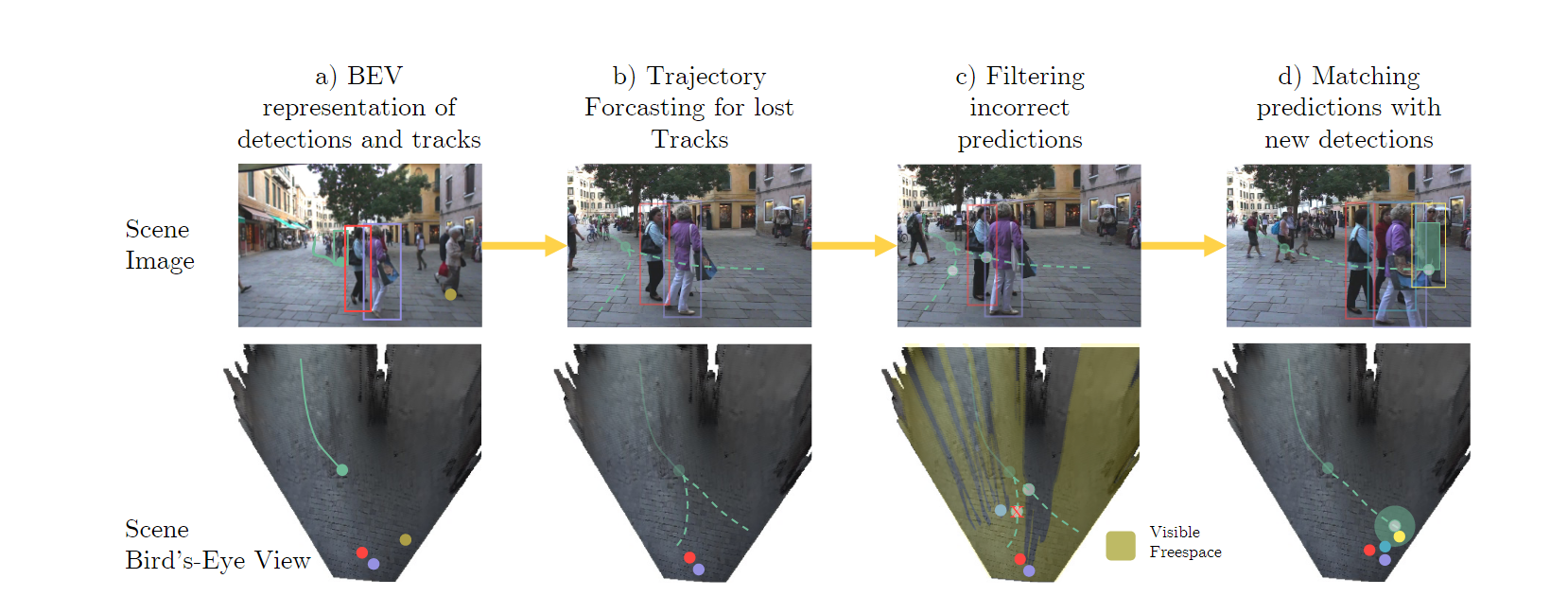
4. 评价

这篇文章可以说也是大力出奇迹的一种, 模型非常复杂, 既有深度估计光流, 也有集成的Social-GAN, 不过利用轨迹预测解决MOT是一种思路, 更接近多模态的感觉.

但仅仅依靠单目2D相机, 估计深度估计的性能也有限.