文生图可控生成之T2I-adapter原理

本文主要是介绍文生图可控生成之T2I-adapter原理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

• 论文：T2I-Adapter: Learning Adapters to Dig out More Controllable Ability for Text-to-Image Diffusion Models
• 代码：TencentARC/T2I-Adapter
• 系列文章：
  • 可控生成之ControlNet原理
  • 可控生成之GLIGEN原理

在前面的文章中，我们介绍过了使用ControlNet来控制文生图模型生成图片，今天介绍将要介绍的T2I-Adapter在功能方面完全与ControlNet一样，但是网络结构完全不同，相比起来更加轻量化，并且个人认为 T2I-Adapter 的网络结构更具有代表性，未来在控制方面有更大的概率都会以 T2I-Adapter 的网络结构呈现，即直接将额外的控制信息直接和 text embedding 一起注入到 Unet 中

1. 动机及贡献

文生图模型近年来已经取得巨大进展，能够生成非常逼真的图片，但是完全使用文本来控制模型生成，并不能充分发挥出模型的性能，本文的目的就是想通过其他控制信息来挖掘文生图模型的能力，从而提升模型更加精细化控制的能力。对此，作者提出了一个简单且轻量化的 T2I-Adapter 来对齐模型内部知识和其他额外的控制信号，这样的话，开发者可以根据不同条件训练多个adapter来实现更加丰富的控制。

T2I-Adapter 作为独立于预训练的文生图模型外的控制网络，具有以下优点：

• 即插即用：它不会改变原始的文生图预训练模型（如SD1.5/ SDXL等）的结构和性能，它作为一种插件存在。
• 简单和轻量化：能够以很小的训练代价与已有的预训练文生图模型结合，整个插件模型只有 77M 的参数，大约只占300M的存储空间
• 灵活使用：可以根据不同的控制条件训练各种adapter，包括颜色、复杂结构的控制等，并且多个adapter可以组合使用，实现更复杂的控制
• 泛化性强：经过一次训练，它可被用在各种以相同base模型finetune后的模型上

2. Method

T2I-Adapter 的整体结构如下图所示，它由一个预训练的SD模型和一些adapters组成，这些adapter用于抽取不同控制条件的特征，预训练的SD模型的参数是固定的，它根据输入的文本特征和其他控制条件特征来生成图片。

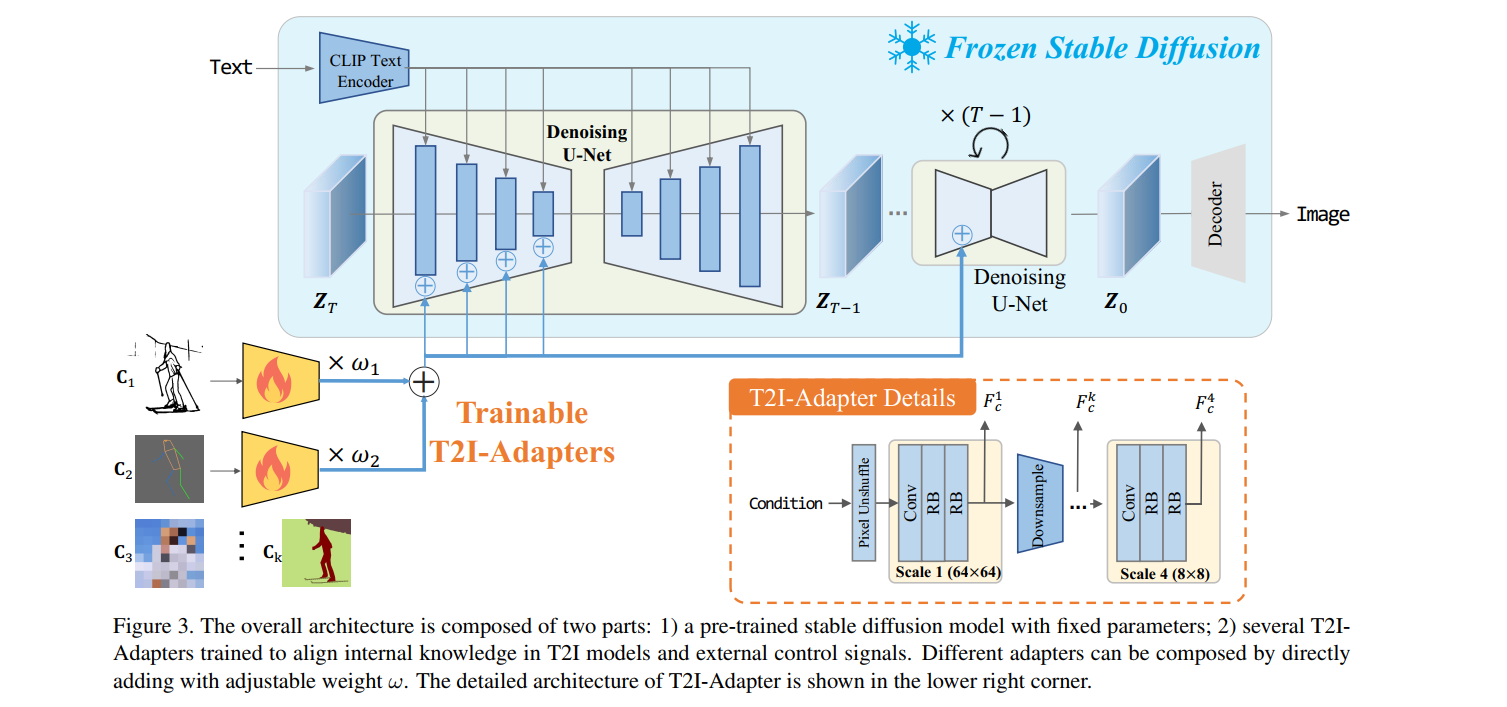
2.1 Adapter 设计

Adapter 设计成了一种轻量化结构，如上图右下角所示，它由4个特征抽取块和3个下采样块组成，控制条件的原始输入分辨率是 $512\times 512$，这里使用了 pixel unshuffle 操作将输入下采样到 $64\times 64$ 分辨率。如上图右下角所示，每个scale中包含一个卷积层和两个残差块，来抽取输入条件的特征 $F_c^k$ ，最终构成多个层面的特征 F c = { F c 1 , F c 2 , F c 3 , F c 4 } \mathbf{F}_c=\{\mathbf{F}_c^1,\mathbf{F}_c^2,\mathbf{F}_c^3,\mathbf{F}_c^4\} Fc​={Fc1​,Fc2​,Fc3​,Fc4​}，注意这里的每个特征 ${\mathbf{F}}_c$ 和输入到Unet中的文本特征 F e n c = { F e n c 1 , F e n c 2 , F e n c 3 , F e n c 4 } \mathbf{F}_{enc}=\{\mathbf{F}_{enc}^1,\mathbf{F}_{enc}^2,\mathbf{F}_{enc}^3,\mathbf{F}_{enc}^4\} Fenc​={Fenc1​,Fenc2​,Fenc3​,Fenc4​}的维度相同。之后，每个层面的特征${\mathbf{F}}_c$ 和 ${\mathbf{F}}_{enc}$ 相加。整个过程可以总结成下式:

F c = F A D ( C ) F ^ e n c i = F e n c i + F c i , i ∈ { 1 , 2 , 3 , 4 } \begin{aligned}\mathbf{F}_c&=\mathcal{F}_{AD}(\mathbf{C})\\\hat{\mathbf{F}}_{enc}^i&=\mathbf{F}_{enc}^i+\mathbf{F}_c^i,i\in\{1,2,3,4\}\end{aligned} Fc​F^enci​​=FAD​(C)=Fenci​+Fci​,i∈{1,2,3,4}​

其中，$C$ 是输入的额外条件，${\mathcal{F}}_{AD}$ 表示 T2I adapter。T2I adapter 能够支持各种结构控制，包括草图、深度图、语义分割图、姿势图等，只需将这些条件输入到adapter中抽取特征即可。

此外，T2I adapter 支持同时多个条件控制，但是这种方法需要额外训练，整个过程可以定义成如下形式：

$${\mathbf{F}}_c=\sum _{k=1}^K{\omega }_k{\mathcal{F}}_{AD}^k({\mathbf{C}}_k)$$

其中 $k\in [1,K]$ 表示第 $k$ 个条件，${\omega }_k$ 是一个可调整的权重，用于调整每个条件的控制强度。

2.2 模型优化与训练

在训练阶段固定SD的参数，只优化adapter的参数。每个训练样本都是一个三元组，包括原始图片$X_0$，文本 prompt $y$，和其他控制条件 $C$。整个优化过程与原始SD相同，其损失函数如下所示：
$${\mathcal{L}}_{AD}={\mathbb{E}}_{{\mathbf{Z}}_0,t,{\mathbf{F}}_c,ϵ\sim \mathcal{N}(0,1)}\left[||ϵ-{ϵ}_{\theta }({\mathbf{Z}}_t,t,\tau (\mathbf{y}),{\mathbf{F}}_c)|{|}_2^2\right]$$

注意在训练期间，时间步$T$的采样，作者使用了非均匀采样。作者在实验中发现，在adapter中加入time embedding 对提升 adapter 的控制能力很有效，然而这种设计需要adapter参与到每一轮的迭代中，这与最初的简单和轻量化的目的相违背，因此作者希望通过一些合适的训练策略来克服这一问题。

把用DDIM在推理采样的阶段分为3部分，如：开始阶段、中间阶段和结尾阶段；作者发现在中间和末尾阶段使用adapter对最终结果的影响很小，这意味着生成结果的主要内容主要依赖于采样的早期阶段。因此，如果在中后期采样到时间步$t$，那么将不使用控制信息。为了增强 adapter 的训练，作者使用了非均匀采样的策略，从而增加时间步 $t$ 落在早期采样阶段的概率，如下所示，作者使用三次方函数来作为时间步 $t$ 的分布：
$$t=(1-(\frac{t}{T}{)}^3)\times T,t\in U(0,T)$$
如下图所示，通过非均匀采样能够更好的控制

3. 实验及结果

3.1 参数设置

• learning rate：1e-5
• batch size: 8
• optimizer: Adam
• base model: SD 1.4

使用 4卡 32G V100 训练了3天。具体的实验数据，不同的控制条件使用数据不同，数据量也不同，可查看论文4.1章节

3.2 模型效果

不同模型对比定性结果如下图所示

不同模型对比定量对比如下表所示

单个adapter控制效果

多个adapter组合控制效果

3.3 消融实验

• 控制信息注入方式
  作者尝试了在Unet的不同层中注入控制信息，最后发现相比decoder部分，encoder部分更适合注入控制信息。每一层都注入信息能够增强控制能力，encoder和decoder都注入控制信息会有更强的控制能力，但是会限制生成图片纹理的丰富性。最终，作者选择将控制信息注入到encoder的所有层中
  
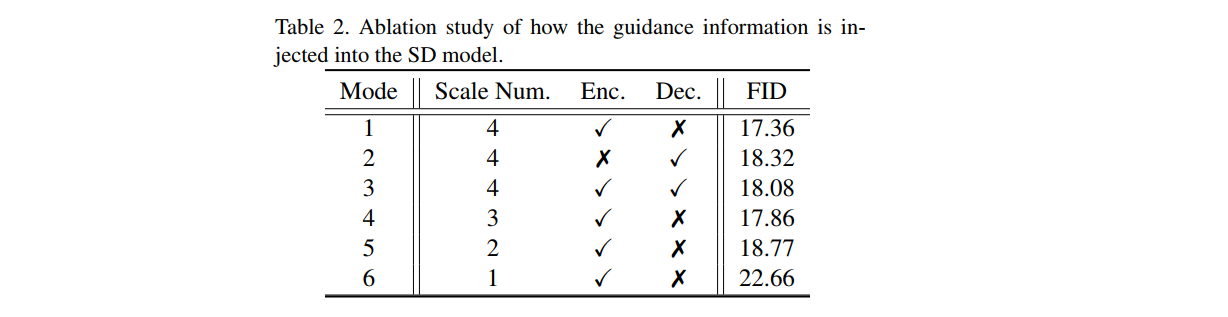
• 模型参数量对控制的影响
  作者通过改变adapter中间特征层的的通道数，来压缩模型的参数量，包括4倍压缩和8倍压缩两种参数量的模型，分别称为 adapter-small（18M 参数） 和 adapter-tiny（5M 参数）。最终发现即使参数变少，仍然有很强的控制能力，如下图所示
  

这篇关于文生图可控生成之T2I-adapter原理的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---