康威生命游戏

康威生命游戏(Game of Life)，剑桥大学约翰·何顿·康威设计的计算机程序。

美国趣味数学大师马丁·加德纳(Martin Gardner，1914-2010）通过《科学美国人》杂志，将康威的生命游戏介绍给学术界之外的广大渎者，一时吸引了各行各业一大批人的兴趣，这时细胞自动机课题才吸引了科学家的注意。这个游戏可以锻炼学生在编程学习路上学以致用，引发生命、哲学思考。建议学过基础算法的同学尝试。

概述

生命游戏没有游戏玩家各方之间的竞争，也谈不上输赢，可以把它归类为仿真游戏。事实上，也是因为它模拟和显示的图像看起来颇似生命的出生和繁衍过程而得名为“生命游戏”。在游戏进行中，杂乱无序的细胞会逐渐演化出各种精致、有形的结构；这些结构往往有很好的对称性，而且每一代都在变化形状。一些形状一经锁定就不会逐代变化。有时，一些已经成形的结构会因为一些无序细胞的“入侵”而被破坏。但是形状和秩序经常能从杂乱中产生出来。

每个方格中都可放置一个生命细胞，每个生命细胞只有两种状态：

“生”或“死”。用黑色方格表示该细胞为“生”，空格(白色)表示该细胞为“死”。或者说方格网中黑色部分表示某个时候某种“生命”的分布图。生命游戏想要模拟的是：随着时间的流逝，这个分布图将如何一代一代地变化。

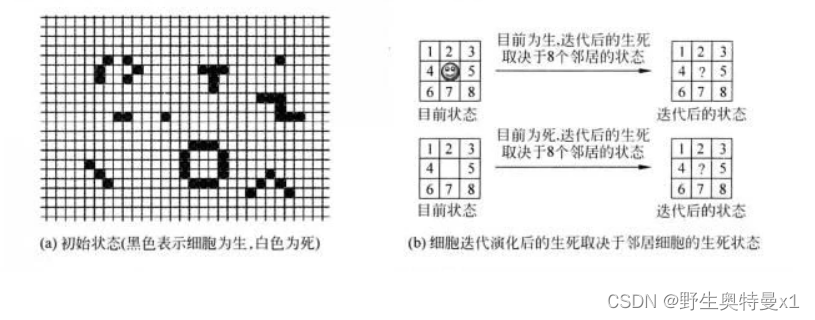
生存定律

游戏开始时，每个细胞随机地设定为“生”或“死”之一的某个状态。然后，根据某种规则，计算出下一代每个细胞的状态，画出下一代细胞的生死分布图。

应该规定什么样的迭代规则呢?需要一个简单的，但又反映生命之间既协同又竞争的生存定律。为简单起见，最基本的考虑是假设每一个细胞都遵循完全一样的生存定律；再进一步，把细胞之间的相互影响只限制在最靠近该细胞的8个邻居中。

也就是说，每个细胞迭代后的状态由该细胞及周围8个细胞状态所决定。作了这些限制后，仍然还有很多方法来规定“生存定律”的具体细节。例如，在康威的生命游戏中，规定了如下生存定律。

(1)当前细胞为死亡状态时，当周围有3个存活细胞时，则迭代后该细胞变成存活状态(模拟繁殖)；若原先为生，则保持不变。

(2)当前细胞为存活状态时，当周围的邻居细胞低于两个(不包含两个)存活时，该细胞变成死亡状态(模拟生命数量稀少)。

(3)当前细胞为存活状态时，当周围有两个或3个存活细胞时，该细胞保持原样。

(4)当前细胞为存活状态时，当周围有3个以上的存活细胞时，该细胞变成死亡状态(模拟生命数量过多)。

可以把最初的细胞结构定义为种子，当所有种子细胞按以上规则处理后，可以得到第1代细胞图。按规则继续处理当前的细胞图，可以得到下一代的细胞图，周而复始。

上面的生存定律当然可以任意改动，发明出不同的“生命游戏”。

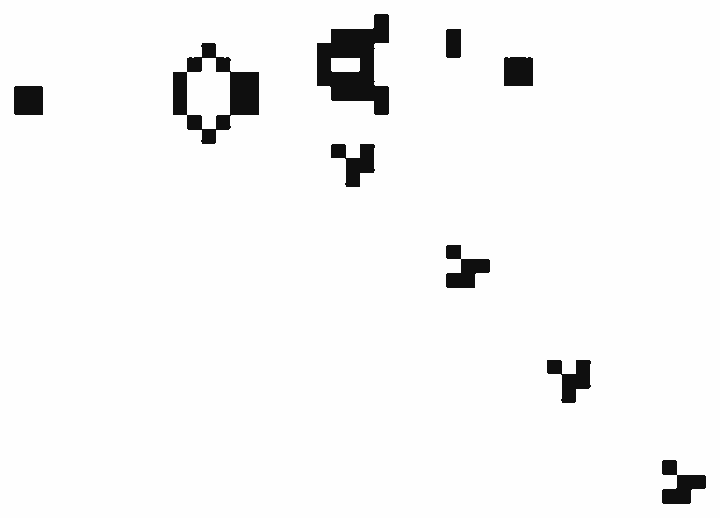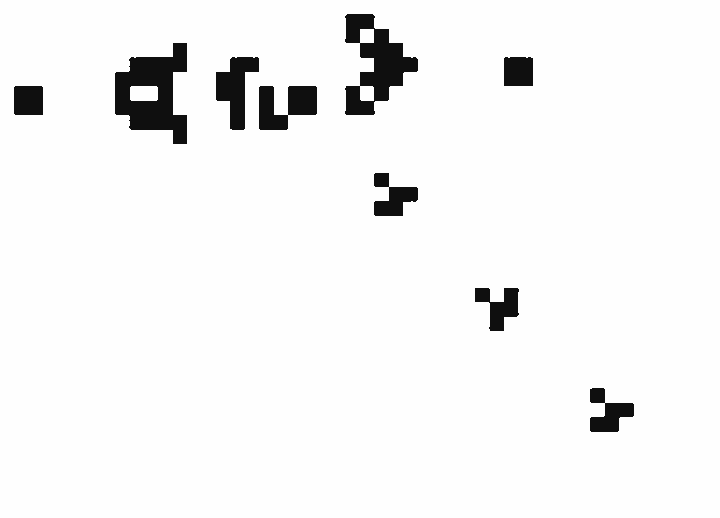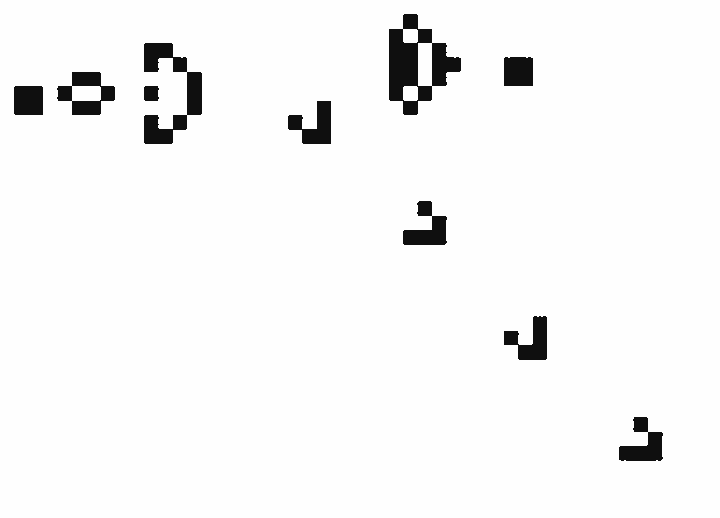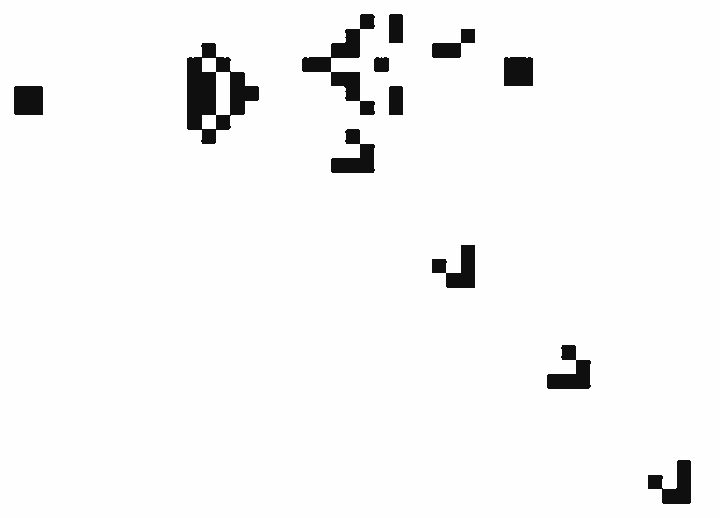
 此游戏源码2天后公布