Cocos2d-x 地图行走的实现2：SPFA算法

本文主要是介绍Cocos2d-x 地图行走的实现2：SPFA算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

　　本文乃Siliphen原创，转载请注明出处：http://blog.csdn.net/stevenkylelee

　　上一节《Cocos2d-x 地图行走的实现1：图论与Dijkstra算法》

　　http://blog.csdn.net/stevenkylelee/article/details/38408253

　　下一节《Cocos2d-x 地图行走的实现3：A*算法》

　　http://blog.csdn.net/stevenkylelee/article/details/38456419

　　本节实践另一种求最短路径算法：SPFA

1.寻路算法实现上的优化

　　上一节我们实现的Dijkstra用了一个哈希表来保存搜索到的路径树。如果能用直接的访问的方式，就不要用哈希表，因为直接访问的方式会比哈希表更快。我们修改一下图顶点的数据结构。如下：

/*图顶点
*/
class Vertex
{friend class Graph ;public:Vertex( const string& Name ){m_strId = Name ;m_pGraph = 0 ;}~Vertex( ) { };public:// 附加数据unordered_map< string , void*> UserData ;public : const unordered_map< string , Edge* >& GetEdgesOut( ) const { return m_EdgesOut ; }const unordered_map< string , Edge* >& GetEdgesIn( ) const { return m_EdgesIn ; }const string& GetId( ) const { return m_strId ; }const string& GetText( ) const { return m_Text ; }void SetText( const string& Text ) { m_Text = Text ; }Graph * GetGraph( ) { return m_pGraph ; }protected: // 出边集合unordered_map< string , Edge* > m_EdgesOut ; // 入边集合unordered_map< string , Edge* > m_EdgesIn ;// 节点表示的字符串string m_Text ; // 节点的IDstring m_strId ; // 所属的图Graph * m_pGraph ; public : // 寻路算法需要的数据struct Pathfinding{// 路径代价估计int Cost ; // 标识符int Flag ;// 顶点的前驱顶点。Vertex * pParent ; Pathfinding( ){Cost = 0 ; Flag = 0 ; pParent = 0 ; }}PathfindingData ;};

　　修改的地方是：把int m_Cost成员变量删掉，末尾增加了一个Pathfinding类型的字段。这个结构体负责保存寻路算法所需要的一些变量。虽然我们可以像这样unordered_map< Vertex* , int > , unordered_map< Vertex* , Vertex*> 动态地为顶点增加一些“临时属性”，但这种做法运行起来比较慢。Pathfinding的pParent字段表示寻路算法执行完后，该顶点到起始顶点的一条”反向路径“，一直查找pParent直到为空，可追溯到起始顶点，这就是一条路径。起始顶点的Pathfinding::pParent肯定为空，因为它就是路径树的根节点。如果非起始顶点的Pathfinding::pParent为空，表示起始顶点到该顶点没有通路。

　　上一节我们实现的Dijkstra是按照Dijkstra算法的思想用最简单的方法直接做的。这样做是为了更简单地表达出算法的思想。Dijkstra的算法优化就是在于怎样做”选出拥有最小路径估计的顶点“。关于这个问题的优化，可以搜索下优先级队列，二项堆，斐波那契堆。

　　std有一个叫 priority_queue 的容器，就是优先级队列。是用priority_queue还是自己写一个优先级队列来优化，你们自己考虑吧。俗话说，师傅领进门，修行靠个人。（什么堆来堆去的数据结构，哥早已忘得一干二净了）

2.SPFA算法介绍

　　SPFA是 Shortest Path Faster Algorithm 的缩写，中文直译过来就是：最短路径快速算法。作用在稀疏图上通常比Dijkstra更快，是一种高效的求最短路径算法。和Dijkstra一样，也是求某个顶点到其他所有顶点的最短路径的一种算法。用我自己理解的话来说，SPFA是这样：

　　2.1.SPFA算法需要什么

　　SPFA需要用到一个先进先出的队列Q。

　　SPFA需要对图中的所有顶点做一个标示，标示其是否在队列Q中。可以用哈希表做映射，也可以为顶点增加一个字段。后者的实现效率更高。

　　2.2.SPFA是怎样执行的

　　2.2.1 SPFA的初始化

　　SPFA的初始化和Dijkstra类似。

　　先把所有顶点的路径估计值初始化为代价最大值。比如：0x0FFFFFFF。

　　所有顶点都标记为不在队列中。

　　起始顶点放入队列Q中。

　　起始顶点标记在队列中。

　　起始顶点的最短路径估计值置为最小值，比如0。

　　然后下面是一个循环

　　2.2.2 SPFA循环

　　循环结束的条件是队列Q为空。第一次进入循环的时候，只有起始顶点一个元素。

　　每次循环，弹出队列头部的一个顶点。

　　对这个顶点的所有出边进行松弛。如果松弛成功，就是出边终点上对应的那个顶点的路径代价值被改变了，且这个被松弛的顶点不在队列Q中，就把这个被松弛的顶点入队Q。注意，这里顶点入队的条件有2：1.松弛成功。2.且不在队列Q中。

　　当队列Q没有了元素。算法结束。

　　2.3.SPFA伪代码

void Spfa( 图G，起始顶点VStart )
{foreach( 对图G中的所有顶点进行遍历,迭代对象v表示遍历到的每一个顶点对象）{设置顶点v的路径代价估计值为代价最大值，例如：0x0FFFFFFF设置标示顶点v不在队列中顶点v的前驱顶点都为空}起始顶点VStart路径代价估计值为最小值0起始顶点VStart入队Qfor( 如果队列Q不为空）{队列Q弹出一个队头元素v记录v已经不在队列Q中了for( 遍历从队列Q中弹出的队头顶点v的每一个出边）{u = 边终点上的顶点 Relax( v , u，边上的权值）if( Relax松弛成功了 && 顶点u不在队列Q中）{u入队Q记录u在队列中了}}}
}

　　从以上伪代码来看，SPFA和BFS很像：都用了队列，都是从队列弹出一个元素进行扩展子节点。SPFA不同于BFS的扩展：SPFA的扩展子节点是有条件的，根据松弛的结果。

3.SPFA算法的实现

　　Dijkstra不需要关心松弛的结果，所以之前的Dijkstra的Relax函数返回值为void。而SPFA是需要知道松弛是否成功的，它根据此结果决定松弛的顶点是否需要入队。所以，我们实现的SPFA的Relax函数需要返回bool。

　　以下，是我的SPFA实现代码

　　Spfa.h

#pragma once#include "Graph\GraphPathfinding.h"class Spfa :public GraphPathfinding
{
public:Spfa( );~Spfa( );public : virtual void Execute( const Graph& Graph , const string& VetexId ) ; private:inline bool Relax( Vertex* pStartVertex , Vertex* pEndVertex , int Weight ) ;};

　　Spfa.cpp

#include "Spfa.h"
#include <queue>
using namespace std ;Spfa::Spfa( )
{
}Spfa::~Spfa( )
{
}void Spfa::Execute( const Graph& Graph , const string& VetexId )
{// 取得图的顶点集合const auto& Vertexes = Graph.GetVertexes( ) ; //  取得起始顶点对象Vertex *pVStart = Vertexes.find( VetexId )->second   ;// Spfa算法需要一个队列保存顶点queue< Vertex* > Q ; // 初始化for ( auto& it : Vertexes ){Vertex *pV = it.second ; pV->PathfindingData.Cost = 0x0FFFFFFF ;//IsInQueue[ pV ] = false ; pV->PathfindingData.Flag = false ;pV->PathfindingData.pParent = 0 ; // 顶点的父路径都设置为空}pVStart->PathfindingData.Cost = 0 ;			// 起始顶点的路径代价为0pVStart->PathfindingData.Flag = true ;		// 起始顶点在队列中//m_Ret.PathTree[ pVStart ] = 0 ;				//  起始顶点的父路径为空Q.push( pVStart ) ;									// 起始顶点先入队// spfa算法for ( ; Q.size( ) ;  ){auto pStartVertex = Q.front( ) ; Q.pop( ) ;	// 队列弹出一个顶点vpStartVertex->PathfindingData.Flag = false ;// 松弛v的所有出边const auto& Eo = pStartVertex->GetEdgesOut( ) ;for ( auto& it : Eo ){auto pEdge = it.second ; auto pEndVertex = pEdge->GetEndVertex( ) ;bool bRelaxRet = Relax( pStartVertex , pEndVertex , pEdge->GetWeight( ) ) ;if ( bRelaxRet ){// 如果对于出边松弛成功，且出边对应的终点顶点不在队列中的话，就插入队尾if ( pEndVertex->PathfindingData.Flag == false ){Q.push( pEndVertex ) ;pEndVertex->PathfindingData.Flag = false ;}}}// end for}// end for}bool Spfa::Relax( Vertex* pStartVertex , Vertex* pEndVertex , int Weight )
{int n = pStartVertex->PathfindingData.Cost + Weight ;if ( n < pEndVertex->PathfindingData.Cost ){// 更新路径代价pEndVertex->PathfindingData.Cost = n ;// 更新路径//m_Ret.PathTree[ pEndVertex ] = pStartVertex ; pEndVertex->PathfindingData.pParent = pStartVertex ;return true ;}return false ; 
}

4.Dijkstra与SPFA在实际上的比较

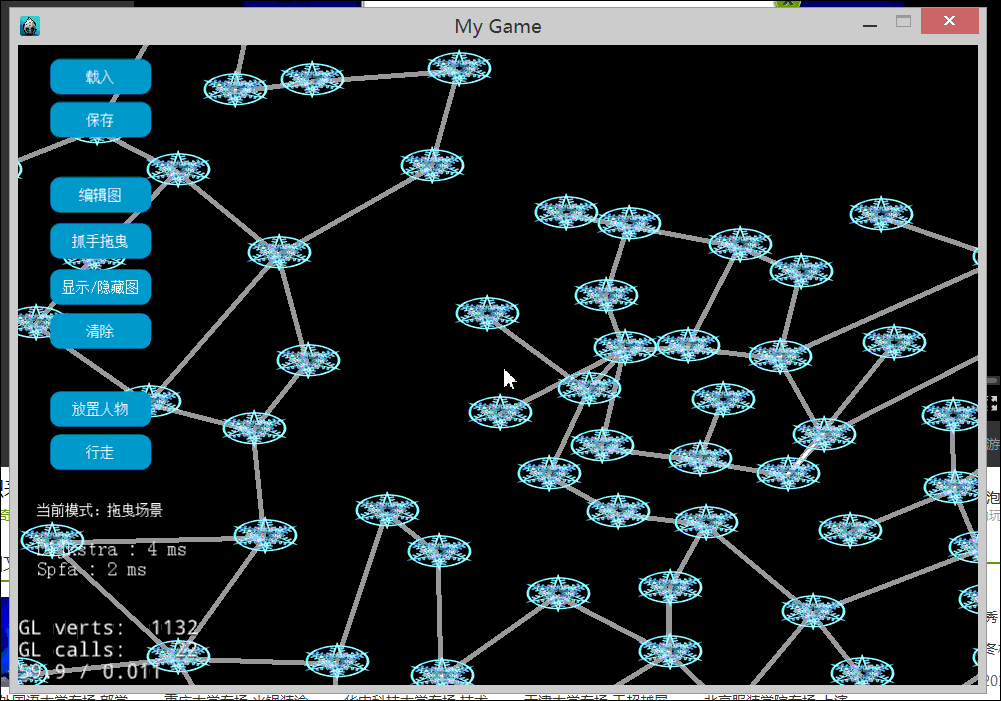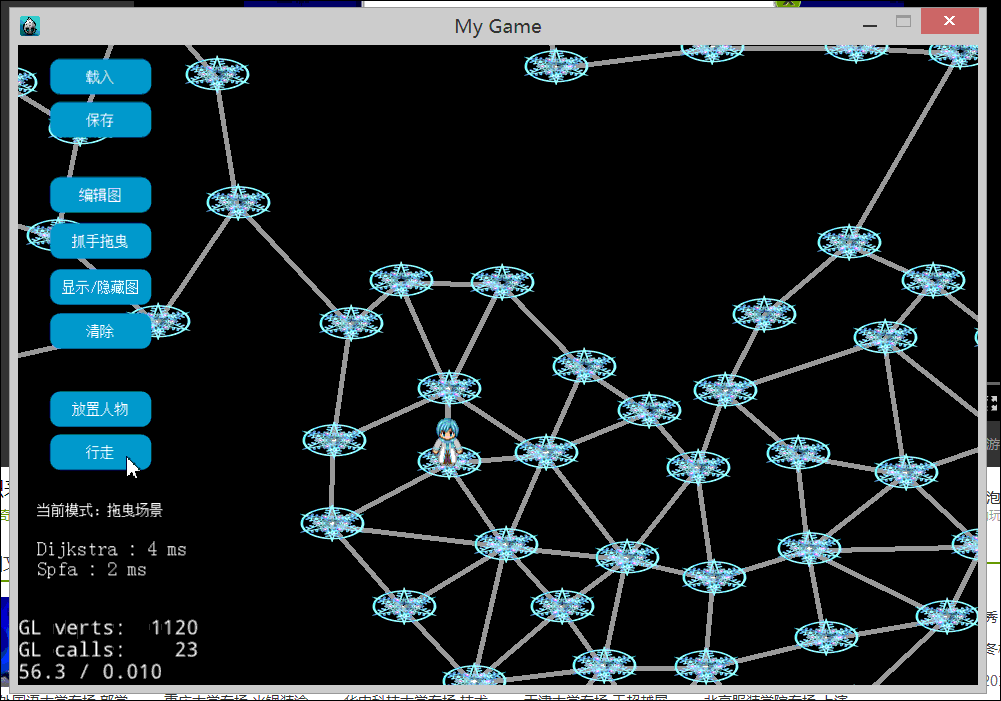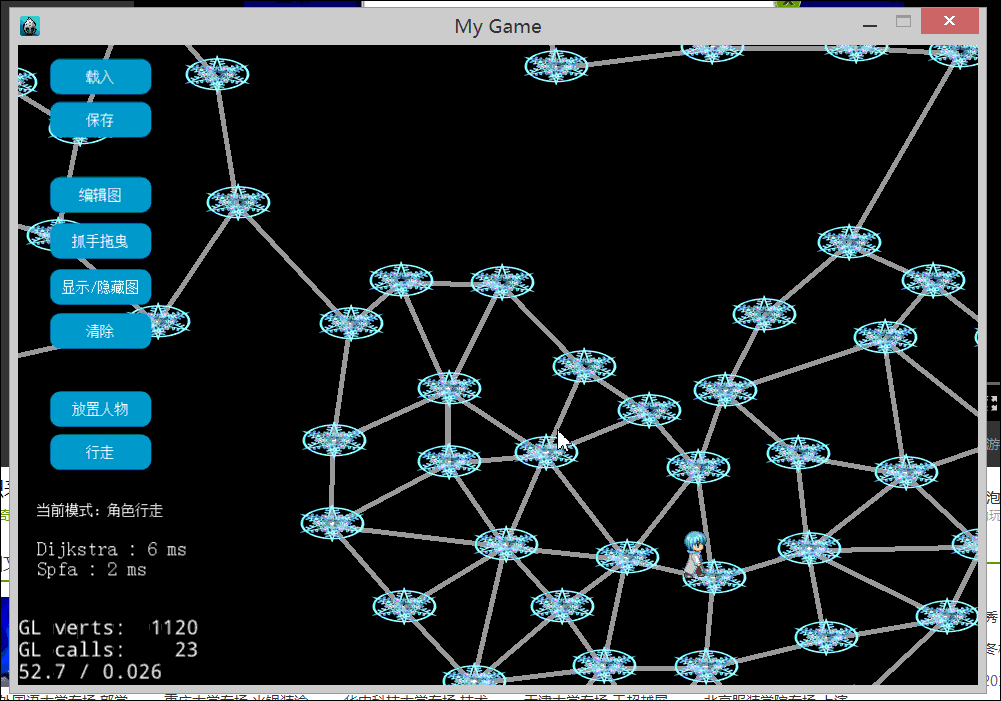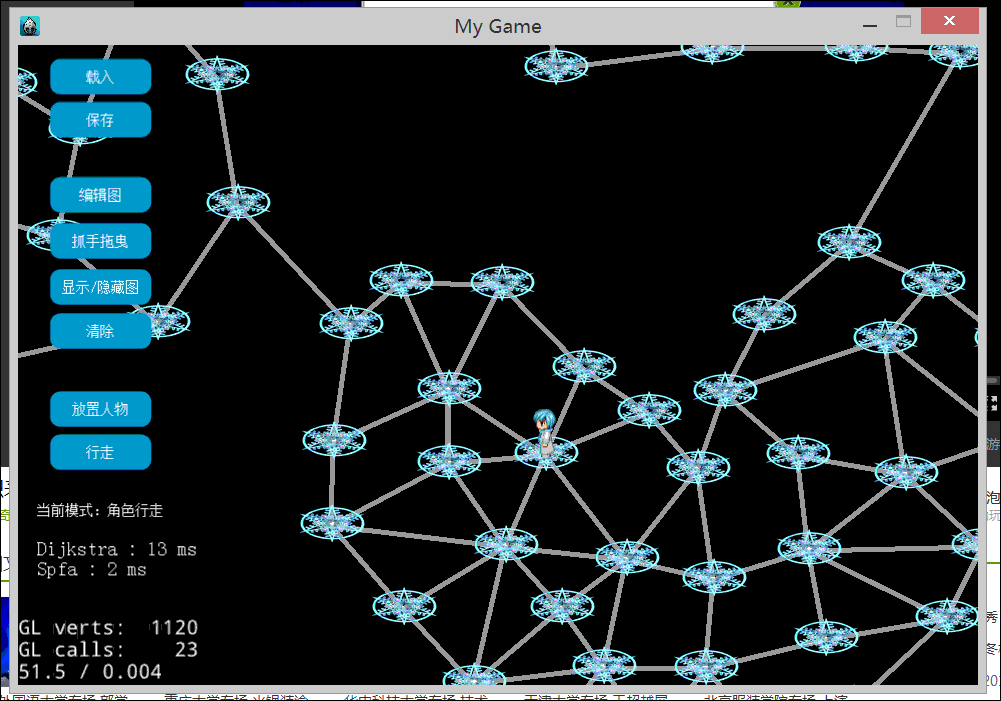
　　下图是构造了一个比较大的图，对于一次寻路同时用了Dijkstra和SPFA。图的左下角显示2个算法所用的时间。

　　对于上图来说，SPFA的执行要快于Dijkstra。当然，是和没有用任何优化的Dijkstra比较的结果。一般来说Dijkstra运行比较稳定，优化后也可以得到不错的性能。而SPFA的优势在于稀疏图，也就是边数较少的图。原因很明显，SPFA不需要像Dijkstra那样去选最小路径代价的顶点出来松弛，它只是从队列里面弹出一个即可。如果边数越少，入队的顶点也就越少。