张维迎《博弈与社会》威胁与承诺（2）序贯理性

本文主要是介绍张维迎《博弈与社会》威胁与承诺（2）序贯理性，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

动态博弈中的理性要求

根据1994年诺贝尔经济学奖得主、德国经济学家泽尔腾（Selten）教授的思想，在一个动态博弈中，参与人如果是理性的，他应该往前看，即不管事前制定的计划如何，他在新的时点上做决策都应该根据当前的情形选择最优的行动。我们可以把动态博弈中的这种理性行为称为序贯理性（sequential rationality），因为它要求参与人在一个接一个的决策节点上都要选择最优行动。这和静态博弈中仅要求参与人在事前一次性选择最优行动相比，要求就更高了。

实际上，如果说“运筹帷幄，决胜于千里之外”体现的是事前制定一个最优行动计划的重要性，那么“将在外，君令有所不受”体现的就是事后调整、伺机而动的重要性。由于事前很难想到所有可能出现的情形，因此事前制定一个最优的行动计划也是非常困难的。这时，事后的权变调整就变得非常重要。对此，我们可以想象这样一种情景，君王把某一行动计划写在一个锦囊中，交给将军，让他面临某一情形时按照锦囊上的“妙计”来行动。但将军出征在外，情况千变万化，如果出现了锦囊上没有规定的情形，该如何办？显然，这时将军要抛弃“锦囊”，根据新的情形，预计对手未来可能采取的行动，然后再决定自己的最优行动。

进一步，如果某一参与人总是序贯理性的，那么他所使用的战略将是由他在每一个时点上的最优行动组成的。换句话说，该战略将不仅是事前最优的，也会是事后最优的，将满足动态一致性的要求，从而不会包含不可置信的威胁。

我们把所有不包含不可置信的行动的战略组成的纳什均衡称为精炼纳什均衡（perfect Nash equilibrium）。这意味着，精炼纳什均衡要求博弈的参与人必须是序贯理性的，因此有时候精炼纳什均衡也被称为序贯均衡。

子博弈

精炼纳什均衡首先必须是一个纳什均衡。而在所有的纳什均衡中，只有那些战略中不包含不可置信威胁的纳什均衡才是精炼纳什均衡。问题是：如何在所有的纳什均衡中找出精炼纳什均衡？

精炼纳什均衡要求参与人是序贯理性的，在每一个决策节点都要选择最优行动。而一个行动是否是最优选择需要比较选择这一行动后最终得到的报酬与选择其他行动的报酬，而这些报酬不仅取决于自己选择的行动，还有赖于其他参与人对自己选择的应对。这意味着从任意一个决策节点开始的决策情形就像是在原有博弈基础上开始一个“新的博弈”。如果我们能够在每一个这样的“新的博弈”上把最优行动都确定下来，所有这些“新的博弈”上的最优行动就构成了原有博弈的精炼纳什均衡。

为了准确刻画这些原有博弈基础上的“新的博弈”，泽尔腾（Selten,1965）引进一个概念：子博弈（subgame）。子博弈是指原博弈中由某一个决策时点开始之后的部分所构成的博弈，它本身可以视为一个独立的博弈，代表的是参与人在博弈过程中某一个决策时点所面临的决策情形。子博弈体现在博弈树上，相当于从博弈树中某一个决策节点出发，保留原有博弈树结构的部分。原博弈可以看成是一个从初始点开始的子博弈。如果一个子博弈起始点不是初始点，可以把它称为原博弈的一个真子博弈（proper subgame）。

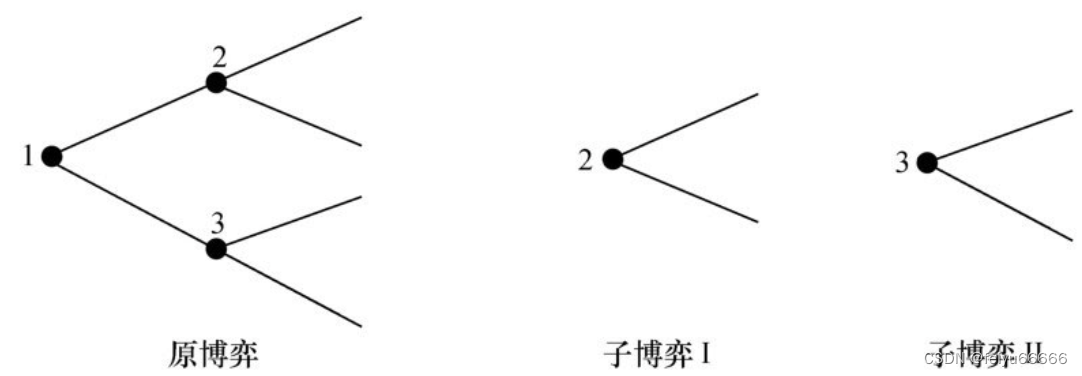
一个具体的例子如图所示。

图中最左侧的博弈表示原博弈，从决策点1开始，如果参与人1选择上面的路径，博弈到达决策点2；如果选择下面的路径，到达决策点3。从决策点2和决策点3开始的博弈，都是原博弈的子博弈。包括原博弈在内，则这个博弈共有3个子博弈。

可以看出，每一个子博弈都代表着参与人所面临的一个决策时机或情形。按照序贯理性的定义，只要博弈的参与人在每一个子博弈上面都选择了最优行动，该参与人一定是序贯理性的。同时，既然子博弈也是一个独立的博弈，那么它也有它的纳什均衡。某一子博弈上的纳什均衡是由所有的参与人在该子博弈上面的最优行动组成的。这就意味着，如果参与人是序贯理性的，其在子博弈上选择的最优行动就一定构成了该子博弈的纳什均衡。若一个博弈有多个子博弈，那么参与人在每一个子博弈上选择的最优行动就构成了相应子博弈上的纳什均衡。显然，由这些每一个子博弈的纳什均衡策略所组成的策略组合也就构成原有博弈的精炼纳什均衡。这样，我们就可以通过逐一确定每一个子博弈上的纳什均衡得到原有博弈的精炼纳什均衡。正因为如此，精炼纳什均衡又被称为子博弈精炼纳什均衡（subgame perfect Nash equilibrium）。

回到前文的师生博弈。该博弈包括原博弈在内总共有三个子博弈。如图所示：

在上图的原博弈中，根据我们前面的分析，总共有三个纳什均衡，分别为：（1）老师选择及格，学生选择（接受，报复）;（2）老师选择不及格，学生选择（报复，接受）;（3）老师选择不及格，学生的战略为（接受，接受）。如前所述，第一个和第二个纳什均衡都包含了不可置信的威胁，第三个则没有。现在，我们来检验一下它们三个是否也都构成了子博弈精炼纳什均衡。

按照子博弈精炼纳什均衡的定义，参与人的战略要在每一个子博弈上都为参与人规定最优的行动。在第一个纳什均衡“老师选择及格，学生选择（接受，报复）”中，老师的战略在其对应的子博弈中（该子博弈实际为原博弈）规定的最优行动为选择及格；学生的战略（接受，报复）分别对应两个子博弈，规定在子博弈I中选择“接受”，在子博弈II中选择“报复”。而在子博弈II中，选择“接受”得到的收益为-1，而选择“报复”为-10，因此“报复”并不是子博弈II上的最优行动。也就是说，学生的战略（接受，报复）并没有在学生的每一个子博弈上都规定最优行动，因此不满足序贯理性。因此，纳什均衡“老师选择及格，学生选择（接受、报复）”也就不是子博弈精炼纳什均衡。

第二个纳什均衡“老师选择不及格，学生选择（报复，接受）”中，学生的战略（报复、接受）规定在学生面临的子博弈I中选择“报复”显然不是最优，也不满足序贯理性的要求。因此该纳什均衡也不是子博弈精炼纳什均衡。

在第三个纳什均衡“老师选择不及格，学生的战略为（接受，接受）”中，老师的战略为不及格，学生的战略为（接受，接受）。学生的这一战略要求学生在子博弈I中选择“接受”，在子博弈II中也选择“接受”。如果老师判及格，学生选择“接受”可以得到1，是最优选择；如果被判不及格，学生选择“接受”可以得到-1，但也是最优选择。这说明学生的战略（接受，接受）在每个子博弈上规定的行动都是最优的。给定学生总会选择“接受”，老师的最优选择就是“不及格”，因此这一纳什均衡是精炼纳什均衡。

逆向归纳与理性共识

上述剔除不可置信威胁的过程，我们是先确定原博弈的纳什均衡，然后检验纳什均衡战略在每一个子博弈中是否构成该子博弈的纳什均衡，以此来确定原博弈的哪一个纳什均衡会构成精炼纳什均衡。这一过程实际上是一种向前展望的顺向推理过程：先确定从起始节点开始的子博弈的最优选择（也就是确定原博弈的纳什均衡），然后顺着博弈发展的方向去确定第二个子博弈、第三个子博弈等的最优选择。但是，如果一个动态博弈阶段较多，这一过程就会比较复杂，甚至会到了很难处理的地步。因此，我们希望能找到一个比较便利的方法来确定子博弈精炼纳什均衡。

根据序贯理性，博弈的参与人在每一个子博弈上都会进行最优选择。那么，他在最后一个子博弈上也会是最优选择，再倒回第二个子博弈点，参与人在这个子博弈上也会进行最优选择。那么，当我们顺着博弈的发展方向难以确定最优选择时，就可以倒着找出每一个子博弈上的最优选择，进行逆向归纳（backward induction），一直到初始决策点。这样找到的战略组合在每个子博弈上都构成一个纳什均衡，从而也是整个博弈的子博弈精炼纳什均衡。

以前述师生博弈为例。回顾上图的3个子博弈。从最右侧的子博弈II倒着开始，学生的最优反应是选择“接受”；然后在子博弈I上面，学生的最优反应也是选择“接受”。这意味着无论老师选择什么，学生都会接受。预期到这一点，回溯到原博弈的初始决策点，老师如果判及格，学生会接受，这时老师得到-1；如果老师判不及格，学生也会选择接受，老师得到1。显然，老师应该选择判不及格。这样，我们从最后一个节点开始逆向归纳，求解出了原博弈的精炼纳什均衡。这比顺向求解快捷多了。

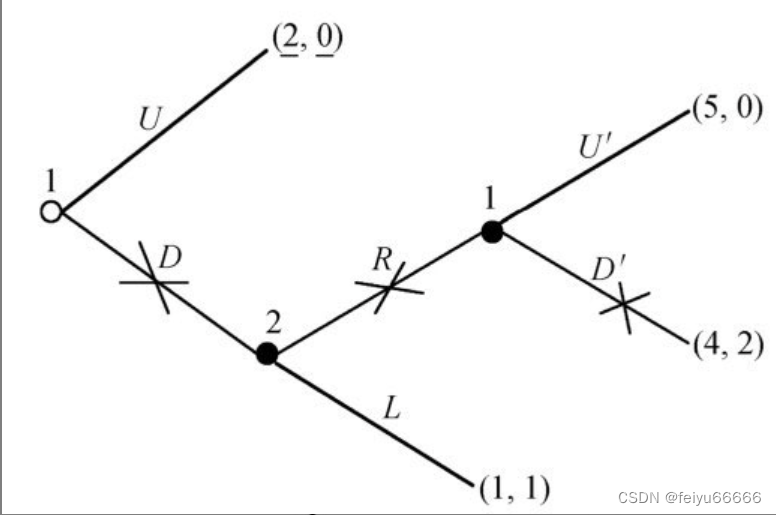
再看如图所示的博弈。

参与人1先选择U或者D（up或down）。如果选U，博弈结束，二人的收益分别为2和0；如果选D，则参与人2接着选择R或者L（right或left）。如果参与人2选择L，博弈结束，二人的收益都为1；如果选择R，参与人1再进行选择U′或D′。如果参与人1选择了U′，二人的收益为5和0；如果选择了D′，则二人的收益为4和2。

我们可以尝试采用逆向归纳来求这个博弈的子博弈精炼纳什均衡。假如博弈进行到最后一个子博弈，从参与人1的第二个决策节点开始。此时参与人1做选择，他选择U′得到5，选择D′得到4，因而他的最优选择为U′。在此子博弈上由于只有一方在做选择，因此其最优选择也是纳什均衡战略。再看倒数第二个子博弈，它从参与人2的决策节点开始。此时由参与人2先行动，选择R或L，然后参与人1再行动，选择U′或D′。那么参与人2如何选择？由于下一步参与人1会选择U′，如果参与人2现在选择R，他最终会得到0；如果参与人2选择L，则得到1。显然，参与人2应该选择L，所以第二个子博弈上的纳什均衡战略组合为（L,U′）。进一步倒推到第一个子博弈（也就是原博弈），从参与人1的第一个决策节点开始。参与人1选择U得到的收益为2；选择D，由于接下来参与人2会选择L，故其收益为1。因此他的最优选择为U。这样，在第一个子博弈上面，参与人1最优战略是（U,U′），参与人2的最优战略为L。因此，战略组合【（U,U′）, L】构成了整个博弈的子博弈精炼纳什均衡（解读为：参与人1首先选择U；如果有第二次选择的机会，选择U′；参与人2如果有机会选择，就选择L）。均衡结果是：参与人1一开始就选择U，参与人2没有任何选择的机会。

逆向归纳的合理性在于我们假定参与人满足第二章讲的理性共识的要求。在这个例子中，参与人1之所以一开始就选择U，是因为他知道第二个人是理性的，如果他选择D就会让参与人2有机会采取行动，且参与人2会选择L。为什么他认为参与人2会选择L？因为他知道参与人2知道如果把机会再留给参与人1，参与人1肯定会选择U′。所以说如果参与人1是理性的，参与人2也是理性的，并且参与人2知道参与人1是理性的，则参与人2就会选择L；如果参与人1知道参与人2知道自己是理性的，参与人1一开始就会选择U。因而，参与人1一开始选择U的合理性，很大程度上取决于理性共识的假设是否成立。这表明，在逆向归纳的过程中，需要假定参与人有理性共识，即每个人都是理性的，而且每个人都知道其他人是理性的，等等。

在现实中，如果参与人不满足理性共识的要求，由逆向归纳得出的结论就可能不符合参与人的实际选择。比如说，如果参与人1不知道参与人2知道自己是理性的，参与人1就很有可能选择D，期待参与人2选择R，自己最后选择U′，从而得到5单位的收益。当然，如果参与人2实际上知道参与人1是理性的，参与人1选择D就只能得到1。现实中，类似的情况确实会发生，所以我们时常会有“早知如此，何必当初”的感叹！

精炼纳什均衡在博弈树上所经过的决策点和最优选择构成一个路径，称为均衡路径（equilibrium path）。相应地，精炼纳什均衡不经过的决策点和选择构成非均衡路径。在上例中，只有节点1和U构成均衡路径。其他路径都是非均衡路径。

不过需要注意的是，均衡路径的构成依赖于参与人在非均衡路径上的选择。比如参与人1选择U之所以会构成均衡路径，是因为参与人2会在非均衡路径上选择L。在师生博弈中，均衡路径是老师选择不及格，学生选择接受，老师得到1，学生得到-1，其他的都是非均衡路径。这个均衡之所以会出现，是因为在非均衡路径上，即使老师判给及格，学生也会接受。这说明非均衡路径上的行为在决定着均衡路径的构成。作个通俗的类比，一个国家之所以选择不对另一个国家发动战争（均衡路径），是因为它预期到一旦爆发战争（非均衡路径），对方会猛烈还击，自己的损失更大。

反事实悖论

精炼纳什均衡战略不仅在均衡路径上是最优的，而且在非均衡路径上也是最优的。也就是说，参与人在不可能事件发生时，也应该按照理性的原则选择最优行动。这就出现了一个悖论：最优战略是基于理性假设做出的，但满足理性假设意味着不可能事件不会发生，如果不可能事件发生了，说明理性假设不成立，在采取下一步的行动时为什么还要假定对方是理性的呢？

在前面图的例子中，如果参与人1选择了D，参与人2应该选择L，因为他预期选择R只能得到0。但如果参与人1真的是理性的，并且知道参与人2也是理性的，也知道参与人2知道自己也是理性的，他就不可能选择D。现在如果他真的选择了D，参与人2为什么还要相信他是理性的并且知道自己（参与人2）也是理性的呢？参与人2会想，一种可能性是参与人1是理性的，但不知道参与人2也是理性的，或者不知道参与人2知道参与人1是理性的。此时，参与人2选择L仍然是最优的。但也有另一种可能：参与人1不是理性的。此时，参与人2选择L就不是最优的，因为非理性的参与人1在最后阶段可能会选择D′。但这又带来了另一个问题：即使参与人1本身是理性的，他也可能选择D以误导参与人1以为他是非理性的，从而有机会在最优阶段选择U′，得到5。但理性的参与人2怎么可能不想到参与人1是假装非理性呢？识破了参与人1的伎俩，参与人2的最优选择仍然是L。但这样一来，参与人1为什么还要假装非理性呢？也就是说，如果你认为一件事是不可能的，它恰恰是可能的；如果你认为一件事是可能的，它恰恰又是不可能的。

这被称为反事实悖论（counter-factual problem）。这是博弈论至今没有解决的难题。泽尔腾的“颤抖手均衡”理论将不可能事件的出现解释为理性的参与人不经意间犯的一个错误（Selten,1975），试图解决这一难题，但并不能完全让人信服。

这篇关于张维迎《博弈与社会》威胁与承诺（2）序贯理性的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---