C++ 数论相关题目，博弈论，SG函数，集合-Nim游戏

本文主要是介绍C++ 数论相关题目，博弈论，SG函数，集合-Nim游戏，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

给定 n
堆石子以及一个由 k
个不同正整数构成的数字集合 S
。

现在有两位玩家轮流操作，每次操作可以从任意一堆石子中拿取石子，每次拿取的石子数量必须包含于集合 S
，最后无法进行操作的人视为失败。

问如果两人都采用最优策略，先手是否必胜。

输入格式
第一行包含整数 k
，表示数字集合 S
中数字的个数。

第二行包含 k
个整数，其中第 i
个整数表示数字集合 S
中的第 i
个数 si
。

第三行包含整数 n
。

第四行包含 n
个整数，其中第 i
个整数表示第 i
堆石子的数量 hi
。

输出格式
如果先手方必胜，则输出 Yes。

否则，输出 No。

数据范围
1≤n,k≤100
,
1≤si,hi≤10000
输入样例：
2
2 5
3
2 4 7
输出样例：
Yes

SG函数：表示当前状态所不能到达状态中最小的自然数。
必胜状态：SG不等于0；
必败状态：SG等于0。
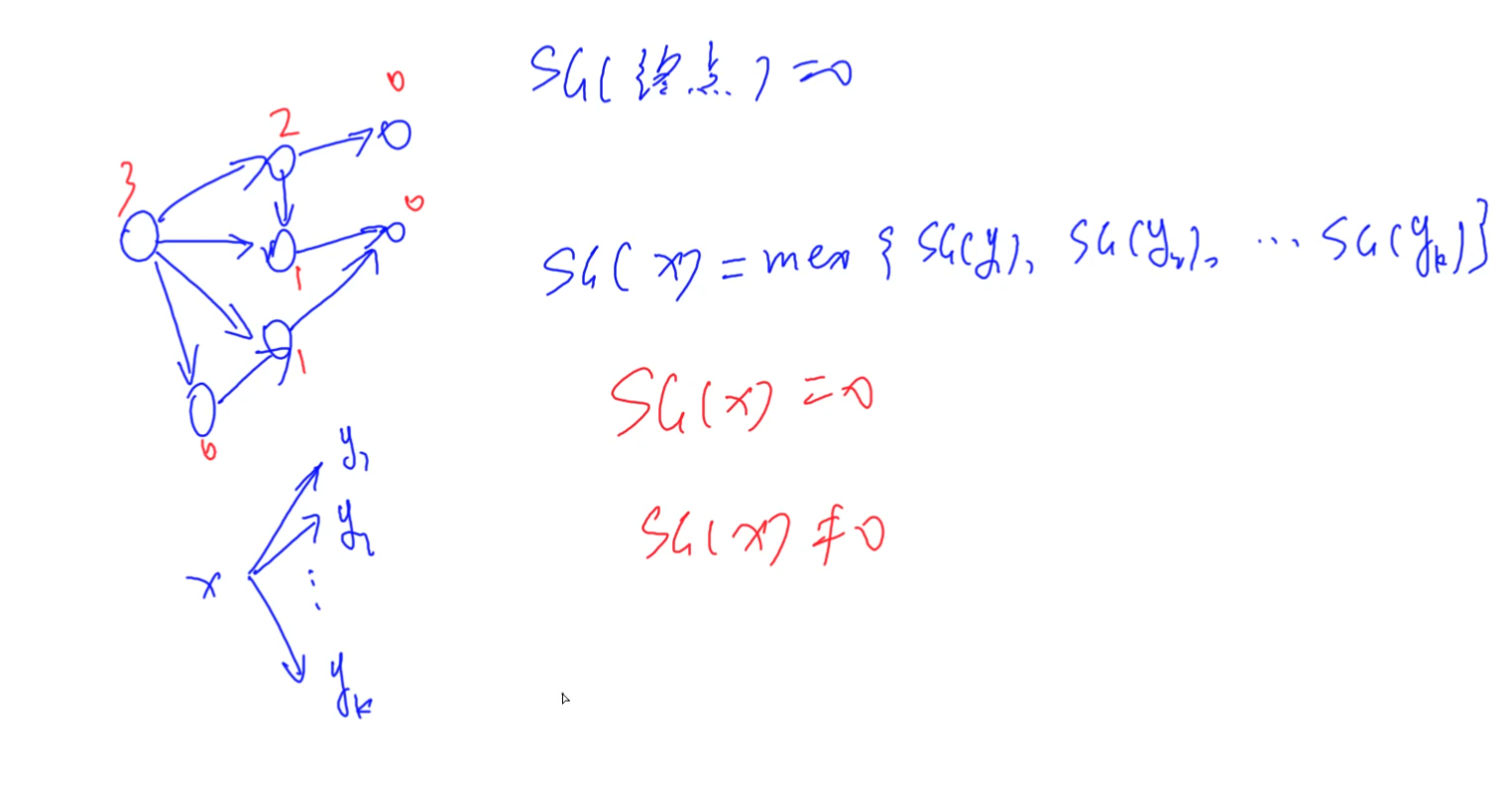
在这里插入图片描述
如果有多个图，将每个初始的SG值异或，等于0必败，不等于0必胜。

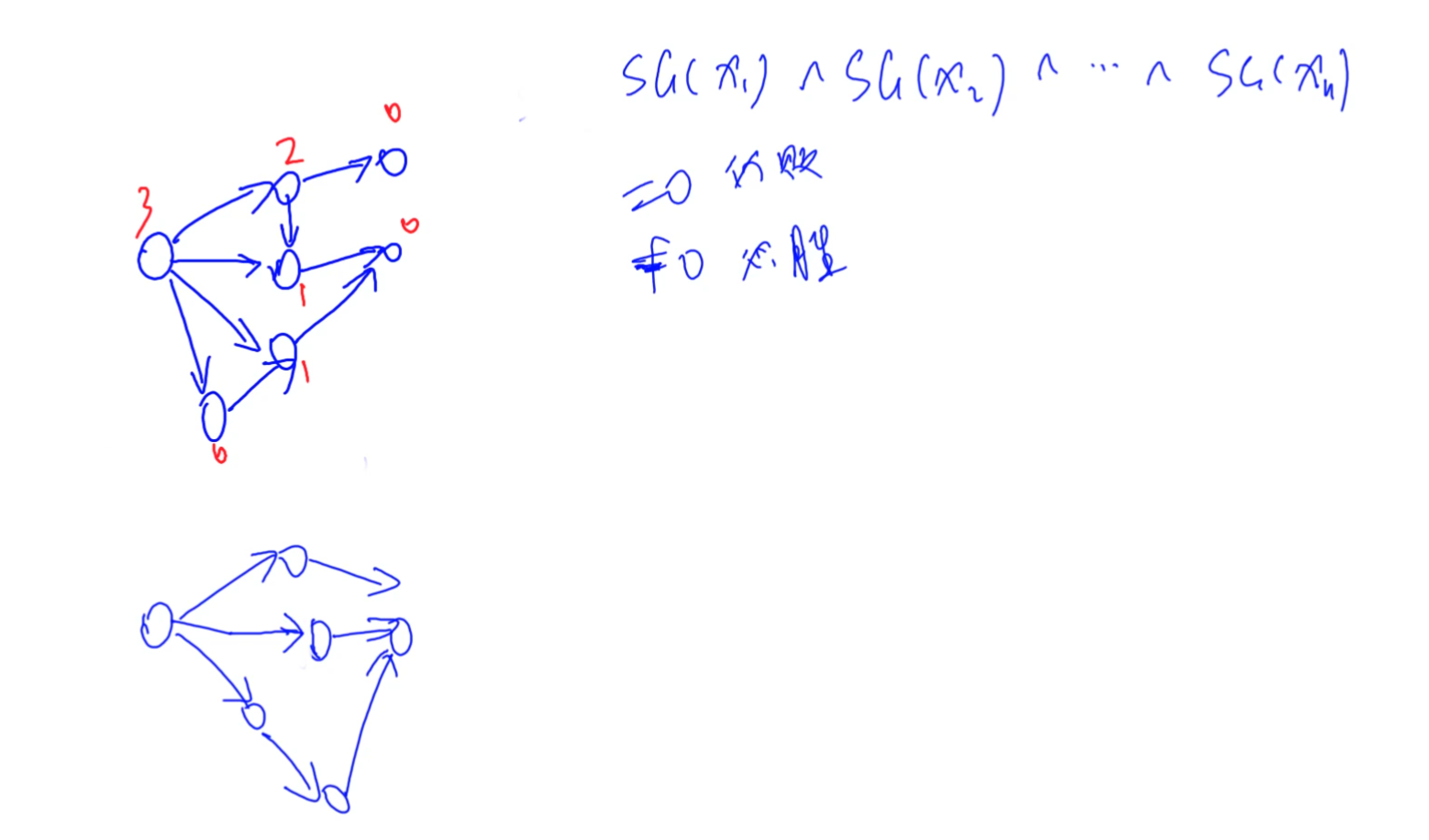
#include <iostream>
#include <cstring>
#include <algorithm>
#include <unordered_set>using namespace std;const int M = 110, N = 10010;int m, n;
int s[M], f[N]; //s存可以取的数，f表明一个状态的sg值，一个状态是一个数，一个确定石子个数的堆可以分解成一个图表示状态。int sg(int x)
{if(f[x] != -1) return f[x]; //避免重复计算，如果x状态算过的话，就直接返回这个状态的sg值unordered_set<int> S;//存能到达的状态的sg值。for(int i = 0; i < m; i ++ ) //遍历每一个图（堆，石子堆）if(x >= s[i])S.insert(sg(x - s[i]));for(int i = 0; ; i ++ )if(!S.count(i)) //找到最小的不存在的状态自然数，说明当前状态的sg值就是i这个数return f[x] = i;}int main ()
{cin>>m;for(int i = 0; i < m; i ++ ) cin>>s[i];cin>>n;memset(f, -1, sizeof f);int res = 0;while(n -- ){int x;cin>>x;res ^= sg(x);}if(res) puts("Yes");else puts("No");return 0;
}