本文主要是介绍P2404 自然数的拆分问题 深度优先搜索,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 题目链接
- 题目描述
- 解题思路
- 代码实现
- 总结
题目链接
链接: P2404 自然数的拆分问题
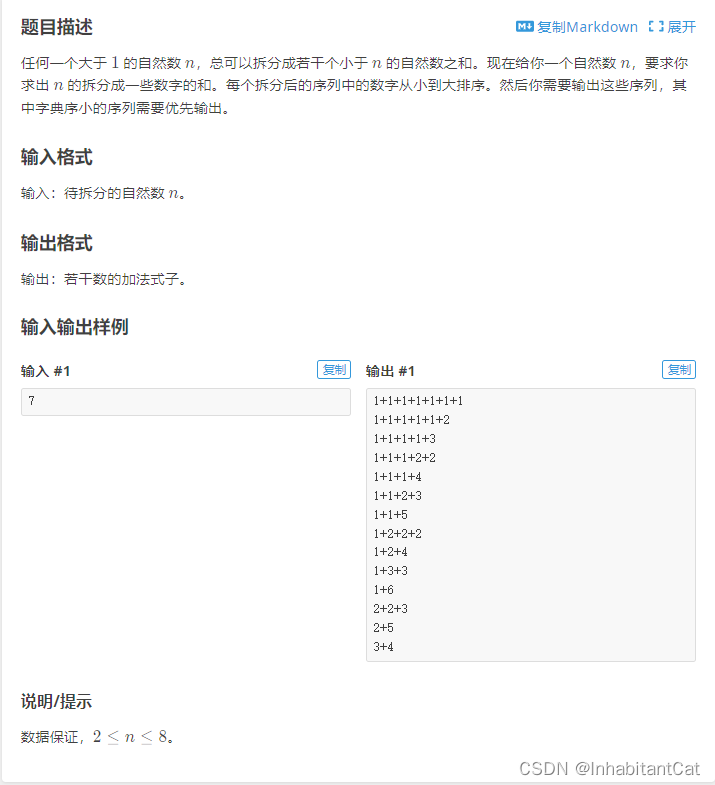
题目描述
解题思路
题目的目标是在给定一个正整数 n 的情况下,找出所有和为 n 的正整数序列(从 1 开始)。具体来说,代码中的dfs函数是一个深度优先搜索(DFS)的实现,用于搜索可能的正整数序列,而主函数则负责接收输入并进行调用。
代码的解题思路及总结如下:
-
DFS搜索所有可能的和为 n 的正整数序列:代码的关键部分是
dfs函数,它通过递归地搜索所有可能的正整数序列,以求得和为 n 的序列。在递归的过程中,当前位置x表示当前从1到x的数的和为n的一种解,参数c表示当前序列的长度。递归的终止条件是当x到达n时,检查当前序列是否满足升序要求,并输出满足条件的序列。 -
选择合适的搜索策略:代码中使用DFS算法来搜索所有可能的正整数序列,通过尝试从 1 开始的每个正整数,来构建可能的序列。在搜索的过程中,利用递归来进行深度搜索,尝试所有可能的组合。
-
实现并调用DFS函数:在主函数中,首先接收输入的正整数 n,然后调用DFS函数,开始搜索可能的序列。DFS函数通过递归搜索所有可能的序列,找出满足和为 n 的序列,并输出结果。
-
复杂度分析:这段代码的时间复杂度是指数级的,因为它需要尝试所有可能的正整数序列,时间复杂度为 O(2^n)。空间复杂度为 O(n),因为需要存储当前搜索的正整数序列。
注意回溯
for(int i=1;i<=n-1;i++){if(x+i<=n){a[c]=i;dfs(x+i,c+1);a[c]=0;}}
代码实现
#include<bits/stdc++.h>
using namespace std;
int n;
int a[10];
void dfs(int x,int c)
{if(x==n){for(int i=1;i<c;i++){if(a[i]<a[i-1])return;}for(int i=0;i<c-1;i++){cout<<a[i]<<"+";}cout<<a[c-1]<<endl;return;}for(int i=1;i<=n-1;i++){if(x+i<=n){a[c]=i;dfs(x+i,c+1);a[c]=0;}}
}
int main()
{cin>>n;dfs(0,0);return 0;
}
总结
总的来说,这段代码的思路是通过DFS算法搜索所有可能的和为 n 的正整数序列,找出满足条件的序列并输出。这种深度搜索的思路可以解决这类组合问题,属于dfs基础题目,适合新手练习
这篇关于P2404 自然数的拆分问题 深度优先搜索的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





