SAC(Soft Actor-Critic)理论与代码解释

本文主要是介绍SAC(Soft Actor-Critic)理论与代码解释，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

参考连接：SAC(Soft Actor-Critic)阅读笔记 - Feliks的文章 - 知乎

理论

序言基础

Q值与V值

在强化学习中，Critic网络可以采用Q值（动作值函数）或V值（状态值函数），具体选择取决于你使用的算法以及问题的特性。

1. Q值（动作值函数）： Critic网络输出每个状态动作对的Q值，表示在给定状态下采取某个动作的预期累积奖励。这种方法通常用于Q-learning和Deep Q Network（DQN）等算法中，其中主要关注最优动作的选择。

2. V值（状态值函数）： Critic网络输出每个状态的V值，表示在给定状态下的预期累积奖励。这种方法通常用于值迭代方法，如异策略（Off-policy）的蒙特卡洛控制和异策略时序差分学习。 V(s) 表示智能体在状态 s 下，从该状态开始直到未来所能获得的累积奖励的期望值。换句话说，它是智能体处于状态 s 时，遵循某种策略所带来的长期回报的估计。

选择Q值还是V值通常取决于你解决的问题。如果你关心在每个状态下选择最优动作，那么使用Q值更为合适。如果你更关心每个状态的价值，而不仅仅是最优动作的话，那么使用V值可能更合适。$Q(s,a)$ 表示智能体在状态 s 下执行动作 a 后，紧接着直到未来的累积奖励的期望值。与 V 值相比，Q 值不仅考虑了状态，还考虑了特定的动作选择。

在一些算法中，如深度确定性策略梯度（Deep Deterministic Policy Gradient，DDPG），使用的是一个Critic网络同时输出Q值和Actor网络的参数。这种情况下，Critic网络的输出可以同时用于评估状态动作对的Q值和评估状态的V值。

算法区别

D4PG（引入分布式的critic，并使用多个actor（learner）共同与环境交互）

TD3（参考了double Q-learning的思想来优化critic，延缓actor的更新，计算critic的优化目标时在action上加一个小扰动）

PPO：依赖于importance sampling实现的off-policy算法在面对太大的策略差异时将无能为力（正在训练的policy与实际与环境交互时的policy差异过大），所以学者们认为PPO其实是一种on-policy的算法，这类算法在训练时需要保证生成训练数据的policy与当前训练的policy一致，对于过往policy生成的数据难以再利用，所以在sample efficiency这条衡量强化学习（Reinforcement Learning, RL）算法的重要标准上难以取得优秀的表现。

SAC

概念

SAC是基于最大熵（maximum entropy）这一思想发展的RL算法，其采用与PPO类似的随机分布式策略函数（Stochastic Policy），并且是一个off-policy，actor-critic算法

将熵引入RL算法的好处为，可以让策略（policy）尽可能随机，agent可以更充分地探索状态空间，避免策略早早地落入局部最优点（local optimum），并且可以探索到多个可行方案来完成指定任务，提高抗干扰能力。

Q函数与V函数

最大化熵强化学习（Maximum Entropy Reinforcement Learning, MERL）

MERL采用了独特的策略模型。为了适应更复杂的任务，MERL中的策略不再是以往的高斯分布形式，而是用基于能量的模型（energy-based model）来表示策略:

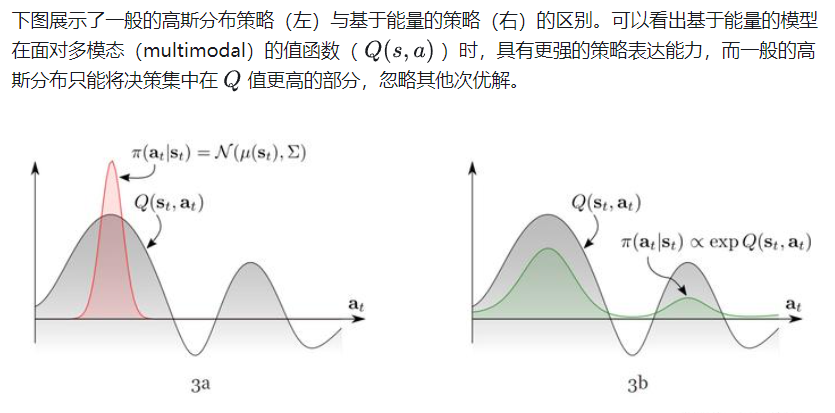
算法流程

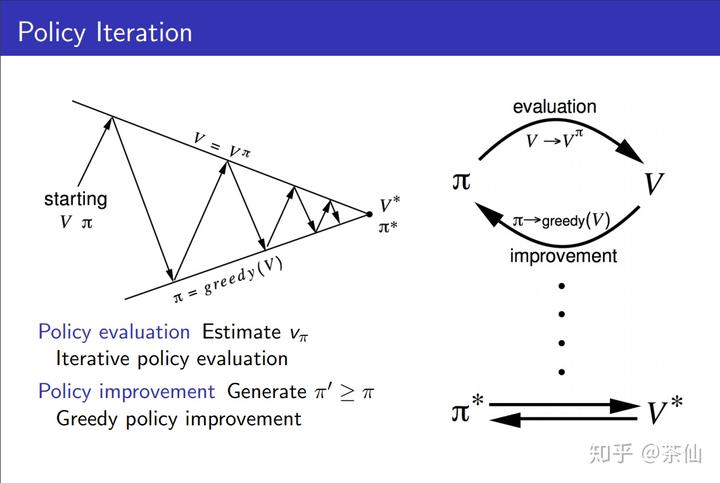
算法同样包括策略评估（Policy Evaluation），与策略优化（Policy Improvement），在这两个步骤交替运行下，值函数与策略都可以不断逼近最优。

1个actor，4个Q Critic

SAC的论文有两篇，一篇是《Soft Actor-Critic Algorithms and Applications》，2018年12月挂arXiv，其中SAC算法流程如下所示，它包括1个actor网络，4个Q Critic网络：（代码使用的是这个：Github链接）

1个actor，2个V Critic，2个Q Critic

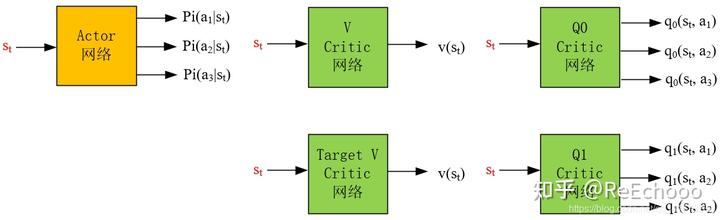
一篇是《Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor》，2018年1月挂arXiv，其中SAC算法流程如下所示，它包括1个actor网络，2个V Critic网络（1个V Critic网络，1个Target V Critic网络），2个Q Critic网络：
参考知乎

代码详解

Actor网络

class Actor(nn.Module):def __init__(self, state_dim, action_dim, hidden_width, max_action):super(Actor, self).__init__()self.max_action = max_actionself.l1 = nn.Linear(state_dim, hidden_width)self.l2 = nn.Linear(hidden_width, hidden_width)self.mean_layer = nn.Linear(hidden_width, action_dim)self.log_std_layer = nn.Linear(hidden_width, action_dim)def forward(self, x, deterministic=False, with_logprob=True):x = F.relu(self.l1(x))x = F.relu(self.l2(x))mean = self.mean_layer(x)log_std = self.log_std_layer(x)  # We output the log_std to ensure that std=exp(log_std)>0log_std = torch.clamp(log_std, -20, 2)std = torch.exp(log_std)dist = Normal(mean, std)  # Generate a Gaussian distributionif deterministic:  # When evaluating，we use the deterministic policya = meanelse:a = dist.rsample()  # reparameterization trick: mean+std*N(0,1)if with_logprob:  # The method refers to Open AI Spinning up, which is more stable.log_pi = dist.log_prob(a).sum(dim=1, keepdim=True)log_pi -= (2 * (np.log(2) - a - F.softplus(-2 * a))).sum(dim=1, keepdim=True)else:log_pi = Nonea = self.max_action * torch.tanh(a)  # Use tanh to compress the unbounded Gaussian distribution into a bounded action interval.return a, log_pi

理论中的训练策略 π($\varphi$) 时的损失函数：

对应代码的：

        # Compute actor lossa, log_pi = self.actor(batch_s)Q1, Q2 = self.critic(batch_s, a)Q = torch.min(Q1, Q2)actor_loss = (self.alpha * log_pi - Q).mean()   ##这里就是关键了撒

Q函数训练时的损失函数：

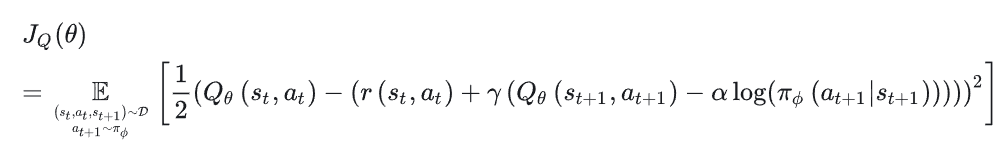
对应代码：

        with torch.no_grad():batch_a_, log_pi_ = self.actor(batch_s_)  # a' from the current policy# Compute target Qtarget_Q1, target_Q2 = self.critic_target(batch_s_, batch_a_)target_Q = batch_r + self.GAMMA * (1 - batch_dw) * (torch.min(target_Q1, target_Q2) - self.alpha * log_pi_)# Compute current Qcurrent_Q1, current_Q2 = self.critic(batch_s, batch_a)# Compute critic losscritic_loss = F.mse_loss(current_Q1, target_Q) + F.mse_loss(current_Q2, target_Q)

温度系数的更新

${\mathcal{H}}_0$ 是预先定义好的最小策略熵的阈值。

        # Update alphaif self.adaptive_alpha:# We learn log_alpha instead of alpha to ensure that alpha=exp(log_alpha)>0alpha_loss = -(self.log_alpha.exp() * (log_pi + self.target_entropy).detach()).mean()self.alpha_optimizer.zero_grad()alpha_loss.backward()self.alpha_optimizer.step()self.alpha = self.log_alpha.exp()

这篇关于SAC(Soft Actor-Critic)理论与代码解释的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---