【洛谷P2486】【BZOJ2243】染色【树链剖分】

本文主要是介绍【洛谷P2486】【BZOJ2243】染色【树链剖分】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目大意：

题目链接：
BZOJ：https://www.lydsy.com/JudgeOnline/problem.php?id=2243
洛谷：https://www.luogu.org/problem/P2486
给出一棵树，维护下列操作：

• $Cabc$：把结点$a$到结点$b$路径上的全部结点染成$c$颜色
• $Qab$：询问结点$a$到结点$b$的颜色段数量。

---

思路：

把一个区间染色就是给线段树上的区间打一个标记，而询问颜色数量也基本来说就是一个普通的查询。所以可以考虑使用树剖。
但是我们发现我们在把树分成一条条的链后，原本的相邻两个点本来可能是相同颜色的，但是剖开之后就分成了两组询问，每组询问都会把这种颜色算一次，但是实际上这一段颜色是只能算一次的。
例如下图

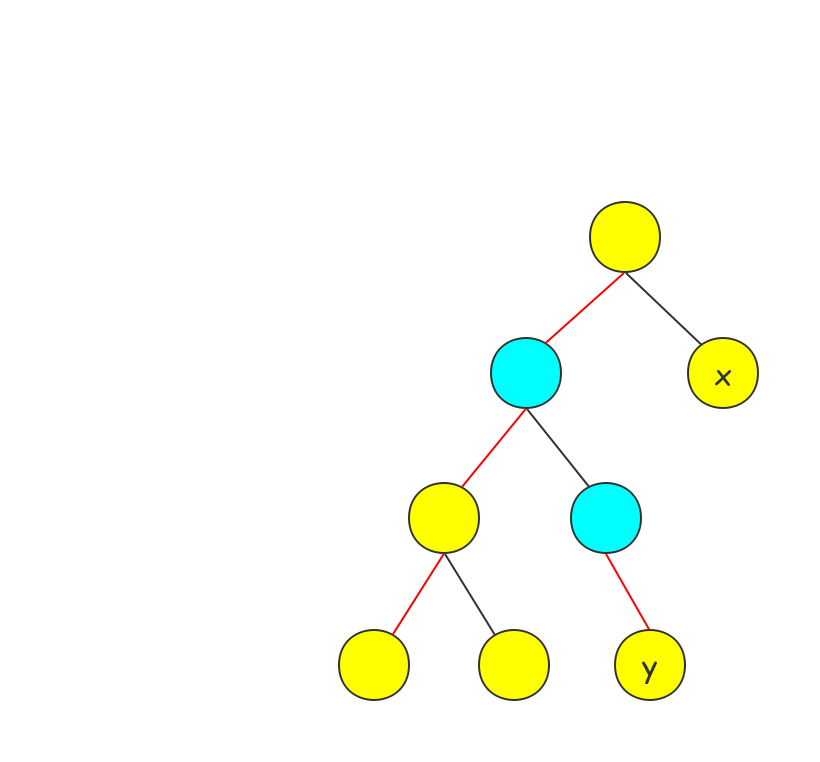
红色的边为重边，此时询问$x,y$之间的颜色段数量，正确答案应该是3，但是我们将蓝点之间的边剖开之后，答案就变成了4。
所以我们需要记录上一条重链的$top$的颜色，如果这个颜色和此时这一条重链的颜色相同，那么答案就要减1。
所以我们设一个$find$函数，用来查询某一个结点的颜色。然后由于是$xy$两个点同时跳，所以我们要记录两条重链的信息。当$xy$位于同一重链后需要进行两次判断。
时间复杂度$O(n{\log }^{2}n)$

---

代码：

为什么我的树剖这么长，同机房的dalao都才140,150行的亚子

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;const int N=100010;
int col[N],son[N],size[N],id[N],rk[N],top[N],fa[N],dep[N],head[N];
int n,m,cnt,tot;
char ch;struct Treenode
{int l,r,lcol,rcol,sum,lazy;
};struct edge
{int next,to;
}e[N*2];struct Tree
{Treenode tree[N*4];void pushup(int x){tree[x].sum=tree[x*2].sum+tree[x*2+1].sum;if (tree[x*2].rcol==tree[x*2+1].lcol) tree[x].sum--;tree[x].lcol=tree[x*2].lcol;tree[x].rcol=tree[x*2+1].rcol;}void pushdown(int x){if (tree[x].lazy){tree[x*2].lazy=tree[x*2+1].lazy=tree[x].lazy;tree[x*2].lcol=tree[x*2].rcol=tree[x*2+1].lcol=tree[x*2+1].rcol=tree[x].lazy;tree[x*2].sum=tree[x*2+1].sum=1;tree[x].lazy=0;}}void build(int x){if (tree[x].l==tree[x].r){tree[x].sum=1;tree[x].lcol=tree[x].rcol=col[rk[tree[x].l]];return;}int mid=(tree[x].l+tree[x].r)>>1;tree[x*2].l=tree[x].l;tree[x*2].r=mid;tree[x*2+1].l=mid+1;tree[x*2+1].r=tree[x].r;build(x*2); build(x*2+1);pushup(x);}void update(int x,int l,int r,int val){if (tree[x].l==l && tree[x].r==r){tree[x].sum=1;tree[x].lcol=tree[x].rcol=tree[x].lazy=val;return;}pushdown(x);int mid=(tree[x].l+tree[x].r)>>1;if (r<=mid) update(x*2,l,r,val);else if (l>mid) update(x*2+1,l,r,val);else update(x*2,l,mid,val),update(x*2+1,mid+1,r,val);pushup(x);}int ask(int x,int l,int r){if (tree[x].l==l && tree[x].r==r) return tree[x].sum;pushdown(x);int mid=(tree[x].l+tree[x].r)>>1;if (r<=mid) return ask(x*2,l,r);if (l>mid) return ask(x*2+1,l,r);int ans1=ask(x*2,l,mid),ans2=ask(x*2+1,mid+1,r);if (tree[x*2].rcol==tree[x*2+1].lcol) return ans1+ans2-1;else return ans1+ans2;}int find(int x,int p){if (tree[x].l==p && tree[x].r==p) return tree[x].lcol;pushdown(x);int mid=(tree[x].l+tree[x].r)>>1;if (p<=mid) return find(x*2,p);else return find(x*2+1,p);}
}Tree;void add(int from,int to)
{e[++tot].to=to;e[tot].next=head[from];head[from]=tot;
}void dfs1(int x,int f)
{fa[x]=f;dep[x]=dep[f]+1;size[x]=1;for (int i=head[x];~i;i=e[i].next){int y=e[i].to;if (y!=f){dfs1(y,x);size[x]+=size[y];if (size[y]>size[son[x]]) son[x]=y;}}
}void dfs2(int x,int tp)
{top[x]=tp;id[x]=++cnt;rk[cnt]=x;if (son[x]) dfs2(son[x],tp);for (int i=head[x];~i;i=e[i].next){int y=e[i].to;if (y!=fa[x] && y!=son[x]) dfs2(y,y);}
}void addrange(int x,int y,int k)
{while (top[x]!=top[y]){if (dep[top[x]]<dep[top[y]]) swap(x,y);Tree.update(1,id[top[x]],id[x],k);x=fa[top[x]];}if (id[x]>id[y]) Tree.update(1,id[y],id[x],k);else Tree.update(1,id[x],id[y],k);
}int ask(int x,int y)
{int ans=0,last[2]={-1,-1},p=0;while (top[x]!=top[y]){if (dep[top[x]]<dep[top[y]]) swap(x,y),p^=1;  //记得交换两条链的编号ans+=Tree.ask(1,id[top[x]],id[x]);if (last[p]==Tree.find(1,id[x])) ans--;  //判断颜色是否相同last[p]=Tree.find(1,id[top[x]]);x=fa[top[x]];}if (dep[x]>dep[y]) swap(x,y),p^=1;ans+=Tree.ask(1,id[x],id[y]);if (last[p^1]==Tree.find(1,id[y])) ans--;if (last[p]==Tree.find(1,id[x])) ans--;  //两条链都要判断return ans;
}int main()
{memset(head,-1,sizeof(head));scanf("%d%d",&n,&m);for (int i=1;i<=n;i++)scanf("%d",&col[i]);for (int i=1,x,y;i<n;i++){scanf("%d%d",&x,&y);add(x,y); add(y,x);}dfs1(1,0); dfs2(1,1);Tree.tree[1].l=1; Tree.tree[1].r=n;Tree.build(1);int x,y,z;while (m--){while (ch=getchar()) if (ch=='C'||ch=='Q') break;if (ch=='C'){scanf("%d%d%d",&x,&y,&z);addrange(x,y,z);}else{scanf("%d%d",&x,&y);printf("%d\n",ask(x,y));}}return 0;
}

这篇关于【洛谷P2486】【BZOJ2243】染色【树链剖分】的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---