数据结构——普里姆（Prim）算法

普里姆算法（Prim算法），图论中的一种算法，可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点，且其所有边的权值之和亦为最小。
以下是数据结构中关于普里姆算法的操作（编程风格参考严蔚敏版数据结构）。

头文件及宏

#include<iostream>
#include<stdio.h>
using namespace std; 
typedef char VerTexType; 
typedef int ArcType; 
#define MaxInt 32767 
#define MVNum 100    
#define OK 1
#define ERROR -1;
typedef int status;

图以及最短边集合的声明

typedef struct{VerTexType vexs[MVNum] {'A','B','C','D','E','F'};ArcType arcs[MVNum][MVNum];int vexnum = 6,arcnum = 10;
}AMGraph; typedef struct{VerTexType adjvex;//最小边在顶点集U的顶点 ArcType lowcost;//最小边上的权值 
}Closedge[MVNum];

特别说明！！！！！
在Closedge中，起点是通过节点VerTexType类型变量表示，而终点是通过下标int类型变量来表示。
adjvex就是某条边的起点，lowcost就是两点之间权值（距离）,closedge[i]里的i是终点的下标。
理解好这个很重要，如果这个理解不好，那就不知道Prim里close辅助数组是怎么用的了。

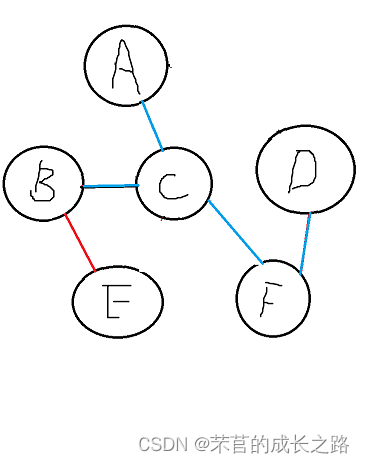
举个例子

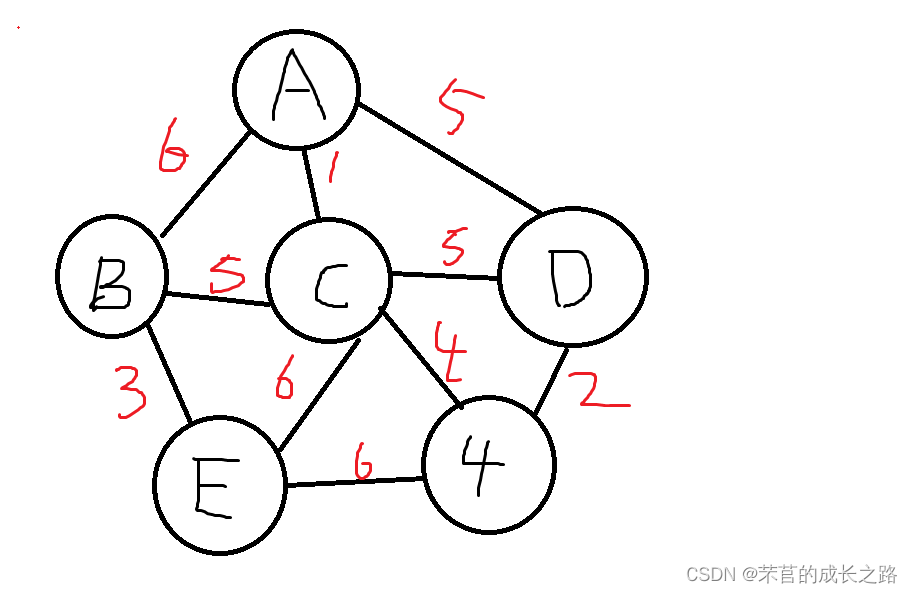
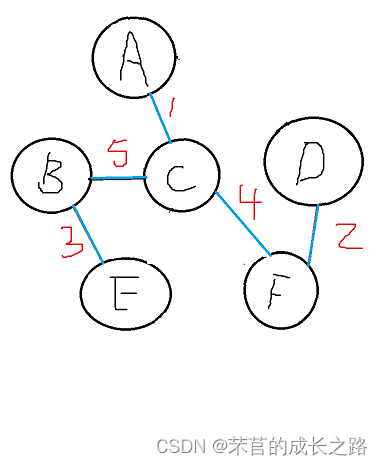
如何算出上图里的最小生成树呢？
老样子先弄出邻接矩阵：

Prim核心算法：

void Prim(AMGraph &G,VerTexType v){int vi = LocateVex(G,v);//获取起始点的下标Closedge close;//辅助数组，用来记录不同点之间的距离以及起始位置（可理解为是一个点边集合） for(int i=0;i<G.vexnum;i++){if(vi!=i){close[i].adjvex=v;close[i].lowcost=G.arcs[vi][i];//初始化辅助数组close,让起点直连其它节点（就是假设起点到全部点的距离都是最短） }else{close[i].lowcost = 0;} } for(int i=1;i<G.vexnum;i++){//i从1开始是因为循环不需要执行vexnum次，不必管节点到自己的距离 int k = Min(close,G);//获取当前点边集合里边权值最小的终点（close里下标表示终点，adjvex表示起点，lowcost表示权值） VerTexType start = close[k].adjvex;//当前边集合里最短边的起点VerTexType end = G.vexs[k];//当前边集合里最短边的终点cout<<start<<"-"<<close[k].lowcost<<"-"<<end<<endl;//输出本次找出来的最短边及端点for(int j=0;j<G.vexnum;j++){//更新close表 if(G.arcs[k][j]<close[j].lowcost){//如果end到j点的距离小于start到j点的距离 //这是以对象的形式简写 close[j] = {G.vexs[k],G.arcs[k][j]};//最短距离从start到j点距离修改成end到j点的距离 //等价于这样写
//				close[i].adjvex=G.vexs[k]; 
//				close[i].lowcost=G.arcs[k][j];}//if}//for } 
}

算法执行过程（红色线表示更新的边，蓝色的表示已被选取的边，黑色的表示当前步骤未被操作的边）：

初始化辅助数组close。这一步目的是让起点直连其它的节点（就是说假设起点到其它全部节点的距离是最短的）。画出来是这样的：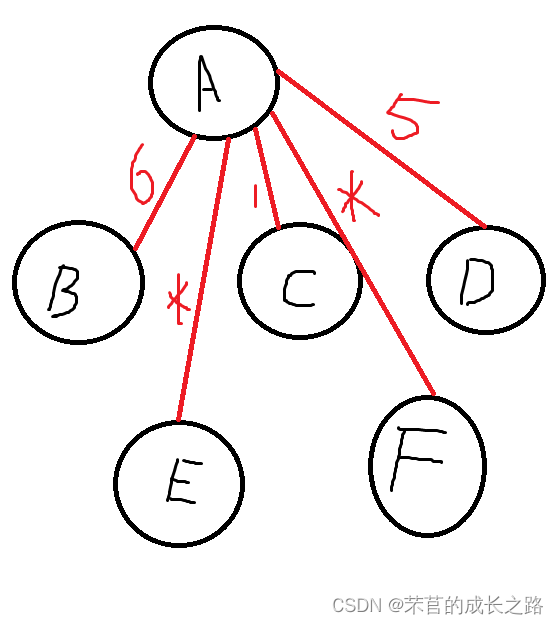
此时的close记录的就是从A到其它全部节点的距离的集合。
开始第一轮循环：在close这些边里选出最短的边，AC的值最小，记录起点为A终点为C（不必做更新操作，因为这条边本就在close里）。然后以AC同时和BEFD比较距离（权值大小）。比如：A到B的距离为为6，C到B的距离是5，close里本来是A到B的边变成C到B，然后close变成如下情况：

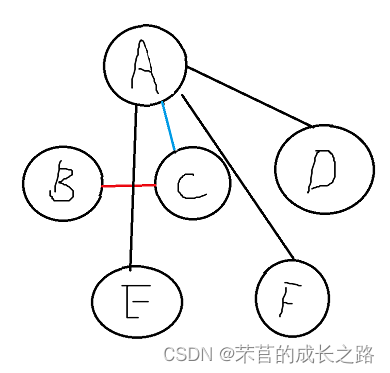
然后AC和E比较，和F比较、和D比较，CE<AE,CF<AF。得出来的close就是这样：

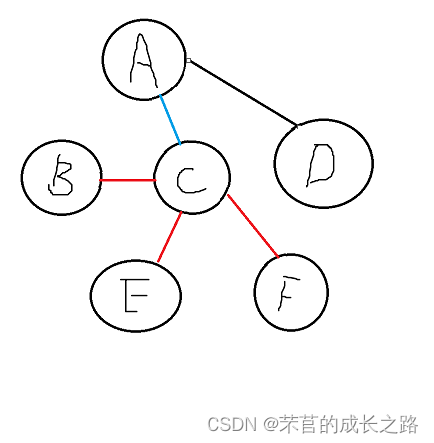
第二轮循环开始：然后选出最短的那条：CF（权值为4）。此时close是这个情况:

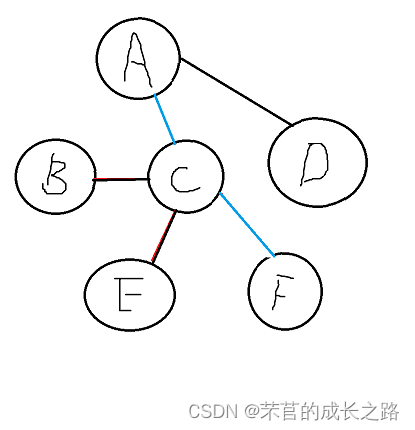
然后A、C、F同时比较距离和B、E、D的距离。CB权值最小close不变，C和F到E距离一致，保持CE相连，FD权值比CD和AD都小，连接FD，更新close。此时的close是这样子的：

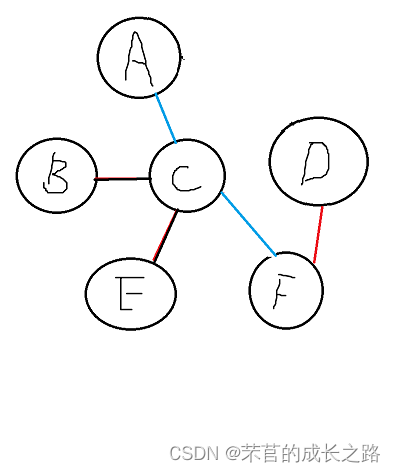
第三轮循环开始：此时的close是这样的：

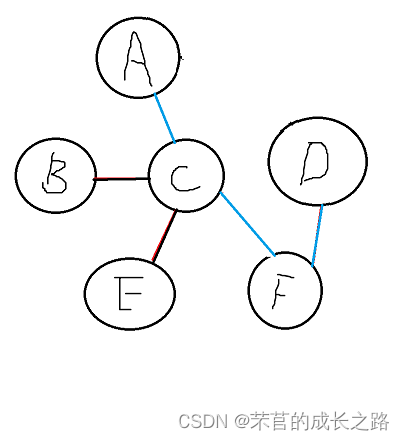
A、C、F、D同时和B、E比较距离：发现是CB最短（但是在2轮循环里CB这条边已经在close里了，就没有实际更新close的操作）
第四轮循环开始：此时的close是这样的：

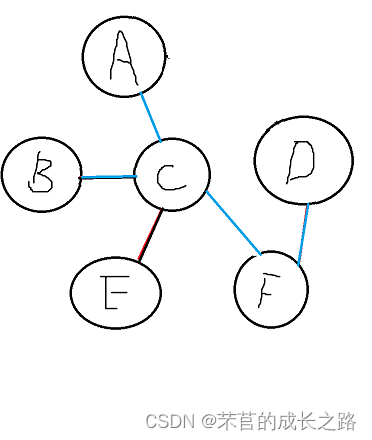
A、B、C、D、F同时与E比较权值：BE的距离比原先的CE短，取消CE更新为BE。此时的close是这个情况：

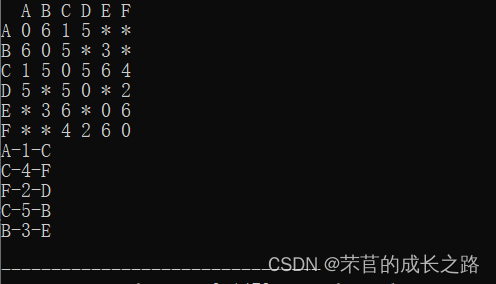
此时最小生成树生成完毕。最后结果如下所示：

代码执行结果：

源码

#include<iostream>
#include<stdio.h>
using namespace std; 
typedef char VerTexType; 
typedef int ArcType; 
#define MaxInt 32767 
#define MVNum 100    
#define OK 1
#define ERROR -1;
typedef int status;typedef struct{VerTexType vexs[MVNum] {'A','B','C','D','E','F'};ArcType arcs[MVNum][MVNum];int vexnum = 6,arcnum = 10;
}AMGraph; typedef struct{VerTexType adjvex;//最小边在顶点集U的顶点 ArcType lowcost;//最小边上的权值 
}Closedge[MVNum];
//其实说白了就是adjvex就是某条边的起点，lowcost就是权值（距离）,closedge[i]的i是终点。
//理解好这个很重要。 
status CreateUDN(AMGraph &G){//创建无向图 	for(int i=0;i<G.vexnum;i++){for(int j=0;j<G.vexnum;j++){if(i==j){G.arcs[i][j] = 0;}elseG.arcs[i][j] = MaxInt;//初始状态全部节点之间相互不可达}}G.arcs[0][1]=6;G.arcs[0][2]=1;G.arcs[0][3]=5;G.arcs[1][2]=5;G.arcs[1][4]=3;G.arcs[2][3]=5;G.arcs[2][4]=6;G.arcs[2][5]=4;G.arcs[3][5]=2;G.arcs[4][5]=6;for(int i=0;i<G.vexnum;i++){for(int j=0;j<G.vexnum;j++){if(G.arcs[i][j]!=MaxInt){G.arcs[j][i] = G.arcs[i][j];} }}//矩阵对称 return OK; 
}void ShowGraph(AMGraph G){cout<<" ";for(int i=0;i<G.vexnum;i++){cout<<" "<<G.vexs[i];}cout<<endl;for(int i=0;i<G.vexnum;i++){cout<<G.vexs[i]<<" ";for(int j=0;j<G.vexnum;j++){if(G.arcs[i][j]==MaxInt){cout<<"* ";}else{cout<<G.arcs[i][j]<<" ";}}cout<<endl;}
}int LocateVex(AMGraph G, VerTexType v){int i;for(i=0;i<G.vexnum;i++){if(G.vexs[i]==v){return i;}} return ERROR;
}int Min(Closedge close,AMGraph G){int min = MaxInt;int mini;for(int i=0;i<G.vexnum;i++){if(min>close[i].lowcost&&close[i].lowcost!=0){//不等于0是指不和自身比较，没意义 min = close[i].lowcost;mini = i; }}
//	cout<<mini<<endl;return mini;
} void Prim(AMGraph &G,VerTexType v){int vi = LocateVex(G,v);//获取起始点的下标Closedge close;//辅助数组，用来记录不同点之间的距离以及起始位置（可理解为是一个点边集合） for(int i=0;i<G.vexnum;i++){if(vi!=i){close[i].adjvex=v;close[i].lowcost=G.arcs[vi][i];//初始化辅助数组close,让起点直连其它节点（就是假设起点到全部点的距离都是最短） }else{close[i].lowcost = 0;//0表示自身或该边已被选取。 } } for(int i=1;i<G.vexnum;i++){//i从1开始是因为循环不需要执行vexnum次，不必管节点到自己的距离 int k = Min(close,G);//获取当前点边集合里边权值最小的终点（close里下标表示终点，adjvex表示起点，lowcost表示权值） VerTexType start = close[k].adjvex;//当前边集合里最短边的起点VerTexType end = G.vexs[k];//当前边集合里最短边的终点cout<<start<<"-"<<close[k].lowcost<<"-"<<end<<endl;//输出本次找出来的最短边及端点for(int j=0;j<G.vexnum;j++){//更新close表 if(G.arcs[k][j]<close[j].lowcost){//如果end到j点的距离小于start到j点的距离 //这是以对象的形式简写 close[j] = {G.vexs[k],G.arcs[k][j]};//最短距离从start到j点距离修改成end到j点的距离 //等价于这样写
//				close[i].adjvex=G.vexs[k]; 
//				close[i].lowcost=G.arcs[k][j];}//if}//for } 
}int main(){AMGraph G;CreateUDN(G);ShowGraph(G);Prim(G,'A'); return 0;
}

关于时间复杂度和空间复杂度

设顶点数n，边数e。邻接矩阵:O(n^2) 邻接表:O(elogn)

敬请批评指正。