哈希概念 | 哈希函数 | 哈希冲突 | 哈希桶实现 | 哈希线性探测代码实现 | 闭散列 | 开散列 | 字符串哈希算法

2024-01-28 16:12
文章标签 算法 代码 实现 函数 字符串 概念 哈希 线性 冲突 探测 闭散列 开散列

本文主要是介绍哈希概念 | 哈希函数 | 哈希冲突 | 哈希桶实现 | 哈希线性探测代码实现 | 闭散列 | 开散列 | 字符串哈希算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

文章目录

        • 1.哈希概念
        • 2.哈希冲突
        • 3.解决哈希冲突
          • 3.1.闭散列
          • 3.2.开散列
        • 4.字符串哈希算法

1.哈希概念

顺序结构以及平衡树中，元素关键码与其存储位置之间没有对应的关系，因此在查找一个元素时，必须要经过关键码的多次比较。如果一个顺序结构，有N个数据，数据之间没有顺序，暴力查找时间复杂度是O（N），但如果数据之间是有序的，就可以使用二分查找能快速的找到查找的值，但是，顺序结构保证有序来存储数据，插入和删除的代价太大！
在这里插入图片描述

对应平衡树来说，查找的时间复杂度O（log2(N)）很优秀！

在这里插入图片描述

但更理想（高效）的方法是：将存储的值和存储的位置一一对应，那么一次就能找到要查找的元素；哈希(散列)方法：通过哈希函数使元素的存储位置与它的关键码之间能够建立一一映射的关系；构造出来的结构称为哈希表(Hash Table)(或者称散列表)

在这里插入图片描述

这样的哈希函数称为 除留余数法；常用的还有，直接定址法。

取关键字的某个线性函数为散列地址：Hash（Key）= A*Key + B，在关键字分分布集中的情况的下使用比较好，但是，如果存储的key范围分散如：arr[] = {1,111,999}要存储这些数据就很麻烦！

我们来看一个直接地址法的例子：字符串中第一个只出现一次字符

题目描述：给定一个字符串 s ，找到 它的第一个不重复的字符，并返回它的索引 。如果不存在，则返回 -1 。如：输入: s = “leetcode” 输出: 0

题目提示：s 只包含小写字母，说明关键字集中。

class Solution {
public:int firstUniqChar(string s) {int temp[256] = {0};for(char ch : s){temp[ch]++;}for(int i = 0; i < s.size();i++){if(temp[s[i]] == 1){return i;}}return -1;}
};
2.哈希冲突

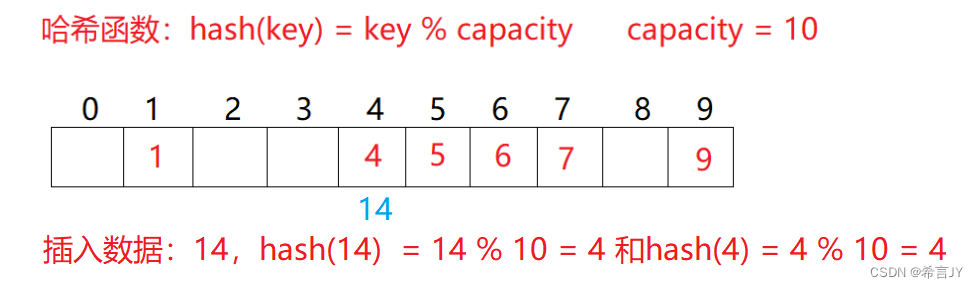
在这里插入图片描述

不同关键字通过相同哈希哈数计算出相同的哈希地址，该种现象称为哈希冲突或哈希碰撞。

3.解决哈希冲突
3.1.闭散列

闭散列：也叫开放定址法，当发生哈希冲突时，如果哈希表未被装满，说明在哈希表中必然还有空位置，那么可以key存放到冲突位置中的下一个空位置中去

下面使用线性探测：从发生冲突的位置开始，依次向后探测，直到寻找到下一个空位置为止。解决哈希冲突的问题，当然还有 二次探测（H_i = (H_0 + i^2 )% m, 或者：H_i = (H_0 - i^2 )% m。其中：i =1,2,3…，H_0是通过散列函数Hash(x)对元素的关键码key 进行计算得到的位置m是表的大小。

在这里插入图片描述

这两种方法，在解决哈希冲突的时候对其他元素产生影响，如：现在要插入数据8，这个位置被14占了，就需要找下一个位置；当然这种方法，也会浪费大量的空间，但这就是用空间换时间的策略，后面开散列才是常用的解决哈希冲突的方法！

在这里插入图片描述

下面快速的使用闭散列的线性探测，实现基于闭散列的哈希表：

代码结构：

namespace order_table
{enum state{EXIST = 1,EMPTY,DELETE};template<class K, class V>struct HashData{std::pair<K, V> _kv;state _st = EMPTY;};template<class K,class V>class HashTable{typedef HashData<K, V> Data;public:HashTable(const size_t size = 5){_table.resize(size);}...private:std::vector<Data> _table;size_t _n = 0;				//  填入表中的元素个数};
}

插入操作：

  1. 通过哈希函数，计算出待插入的位置，如果没有哈希冲突（也就是说判断这个位置有没有插入的值了）直接插入，这里定义一个枚举类型来判断状态
  2. 如果哈希冲突，使用线性探测的方式，寻找下一个空位置！
  3. 在插入之前其实有一个重要的扩容问题，哈希表什么时候扩容呢？ 哈希表的载荷因子定义为：α = 填入表中的元素个数 / 哈希表的长度；α 越大说明，填入表中的元素个数越多，哈希冲突的概率就会越大，所以在开放定址法中α严格定义在0.7 - 0.8之间！
  4. 哈希表扩容是会重新遍历，所以在扩容的那一下会消耗大一些
bool insert(const std::pair<K, V>& kv)
{// 查找一下，不添加重复的元素if (find(kv.first)){return false;}// 扩容if ((double)_n / (double)_table.size() >= 0.7){size_t newsize = _table.size() * 2;HashTable tb(newsize);for (int i = 0; i < _table.size(); i++){if (_table[i]._st == EXIST){tb.insert(_table[i]._kv);}}_table.swap(tb._table);}// 通过哈希函数，计算出待插入的位置，int hashi = kv.first % _table.size();// 线性探测，避免哈希冲突while (_table[hashi]._st == EXIST){hashi++;hashi %= _table.size();}_table[hashi]._kv = kv;_table[hashi]._st = EXIST;_n++;return true;
}

查找操作

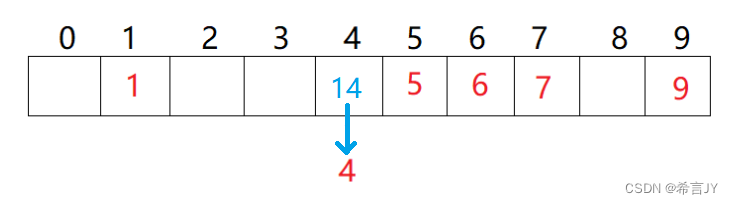
  1. 查找hash表中的元素，通过哈希函数计算初步计算出了查找的位置，EXIST存在但有可能不是查找的元素，如查找14，计算到了4这个位置，但是不是要找元素，另外，当找到状态为DELETE是不能停下来的！要找到下一个空（EMPTY）位置！

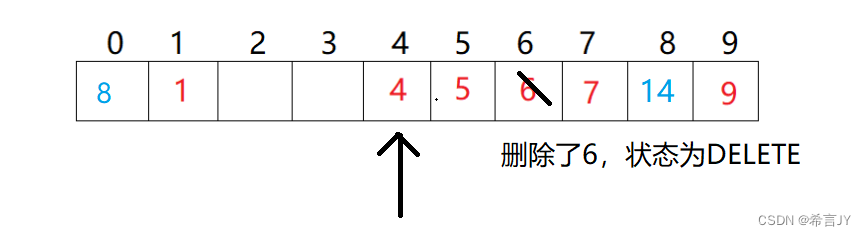
    在这里插入图片描述

  2. 如果找到下一个空（EMPTY）位置说明，哈希表中不存在该元素！

Data* find(const K& key)
{int hashi = key % _table.size();while (_table[hashi]._st != EMPTY){if (_table[hashi]._st == EXIST && _table[hashi]._kv.first == key){return &_table[hashi];}hashi++;hashi %= _table.size();}return nullptr;
}

删除操作

  1. 查找的逻辑，然后，将状态置成DELETE即可。
bool erase(const K& key)
{Data* data = find(key);if (data != nullptr){data->_st = DELETE;_n--;return true;}return false;
}
3.2.开散列

开散列法又叫链地址法(开链法)，或称为哈希桶开辟一个指针数组，通过哈希函数计算关键字，出现哈希冲突时，将冲突的元素通过单链表的方式链接。

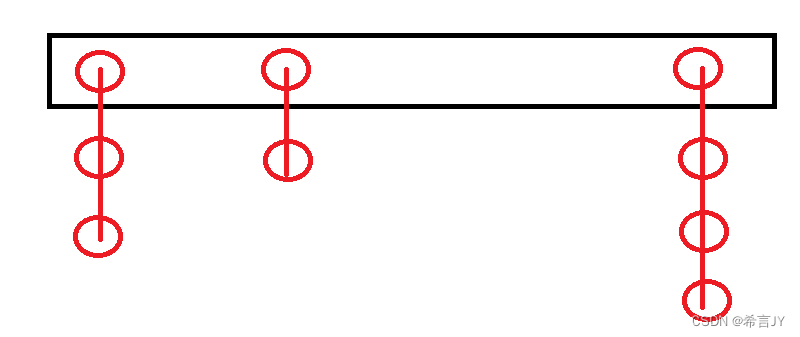
在这里插入图片描述

代码结构：

namespace hash_backet
{template<class K,class V>struct HashNode{std::pair<K, V> _kv;HashNode* _next;HashNode(const std::pair<K, V>& kv):_kv(kv),_next(nullptr){}};template<class K,class V>class HashTable{typedef HashNode<K, V> Node;public:HashTable(const size_t size = 5){_table.resize(size, nullptr);}...private:std::vector<Node*> _table;size_t _n = 0;				//  填入表中的元素个数};
}

插入操作：

  1. 考虑扩容，由于使用哈希桶的方式解决哈希冲突的问题，是以链表的方式，对冲突元素进行链接，冲突不对影响其他元素，所以平衡因子 = 1时扩容

  2. 扩容使用现代方法，即重新开辟一个哈希表对象，将旧表元素插入新表中，然后旧表和新表交换！

  3. 哈希冲突时使用头插法

    在这里插入图片描述

bool insert(const std::pair<K,V> kv)
{// 避免插入重复元素if (find(kv.first)){return false;}if (_n / _table.size() >= 1){size_t new_size = _table.size() * 2;HashTable<K, V> new_table(new_size);for (int i = 0; i < _table.size(); i++){Node* cur = _table[i];while (cur){new_table.insert(cur->_kv  );cur = cur->_next;}}_table.swap(new_table._table);}int hashi = kv.first % _table.size();// 插入逻辑Node* new_node = new Node(kv);Node *cur = _table[hashi];_table[hashi] = new_node;new_node->_next = cur;_n++;return true;
}

查找操作

Node* find(const K& key)
{int hashi = key % _table.size();Node* cur = _table[hashi];while (cur){if (cur->_kv.first == key){return cur;}cur = cur->_next;}return nullptr;
}

删除操作

  1. 如果为NULL不用删除，返回fasle；如果删除1，即_table[hashi]这个位置，置为NULL然后删除；如果删除4，那么4位置出为cur，prev = _table[hashi]；prev-> _next = cur-> _next，然后delete删除cur
    在这里插入图片描述
bool erase(const K& key)
{int hashi = key % _table.size();Node* cur = _table[hashi];Node* prev = nullptr;while (cur){if (cur->_kv.first == key){if (prev == nullptr){_table[hashi] = cur->_next;}else{prev = cur->_next;}delete(cur);_n--;return true;}prev = cur;cur = cur->_next;}return false;
}
4.字符串哈希算法

如果你完整的实现了上面的代码，那么使用哈希函数：int hashi = key % _table.size();时会发现，这个哈希函数只能对能整形进行计算！

如何能对浮点数和字符串进行哈希计算呢

template<class K>
struct DefaultHashFunc
{size_t operator()(const K& key){return (size_t)key;}
};template<>
struct DefaultHashFunc<std::string>
{size_t operator()(const std::string& key){size_t hash = 0;for (char ch : key){hash = hash * 131 + ch;}return hash;}
};

这样就支持了！关于哈希字符串函数算法：参考博客，完整的哈希桶的实现代码

namespace hash_backet
{	template<class K>struct DefaultHashFunc{size_t operator()(const K& key){return (size_t)key;}};template<>struct DefaultHashFunc<std::string>{size_t operator()(const std::string& key){size_t hash = 0;for (char ch : key){hash = hash * 131 + ch;}return hash;}};template<class K,class V>struct HashNode{std::pair<K, V> _kv;HashNode* _next;HashNode(const std::pair<K, V>& kv):_kv(kv),_next(nullptr){}};template<class K,class V>class HashTable{typedef HashNode<K, V> Node;public:HashTable(const size_t size = 5){_table.resize(size, nullptr);}bool insert(const std::pair<K,V> kv){// 避免插入重复元素if (find(kv.first)){return false;}if (_n / _table.size() >= 1){size_t new_size = _table.size() * 2;HashTable<K, V> new_table(new_size);for (int i = 0; i < _table.size(); i++){Node* cur = _table[i];while (cur){new_table.insert(cur->_kv  );cur = cur->_next;}}_table.swap(new_table._table);}DefaultHashFunc<K> dtf;size_t hashi = dtf(kv.first )% _table.size();// 插入逻辑Node* new_node = new Node(kv);Node *cur = _table[hashi];_table[hashi] = new_node;new_node->_next = cur;_n++;return true;}bool erase(const K& key){DefaultHashFunc<K> dtf;size_t hashi = dtf(key )% _table.size();Node* cur = _table[hashi];Node* prev = nullptr;while (cur){if (cur->_kv.first == key){if (prev == nullptr){_table[hashi] = cur->_next;}else{prev = cur->_next;}delete(cur);_n--;return true;}prev = cur;cur = cur->_next;}return false;}Node* find(const K& key){DefaultHashFunc<K> dtf;size_t hashi =  dtf(key) % _table.size();Node* cur = _table[hashi];while (cur){if (cur->_kv.first == key){return cur;}cur = cur->_next;}return nullptr;}void print(){for (int i = 0; i < _table.size(); i++){printf("%d:", i);Node* data = _table[i];while (true){if (data== nullptr){std::cout << "NULL" << std::endl;break;}else{std::cout << data->_kv.second << "-->";data = data->_next;}}}}private:std::vector<Node*> _table;size_t _n = 0;				//  填入表中的元素个数，用于计算平衡因子};
}

这篇关于哈希概念 | 哈希函数 | 哈希冲突 | 哈希桶实现 | 哈希线性探测代码实现 | 闭散列 | 开散列 | 字符串哈希算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/654128。

相关文章

Python函数作用域示例详解

Python函数作用域示例详解

《Python函数作用域示例详解》本文介绍了Python中的LEGB作用域规则,详细解析了变量查找的四个层级,通过具体代码示例,展示了各层级的变量访问规则和特性,对python函数作用域相关知识感兴趣... 目录一、LEGB 规则二、作用域实例2.1 局部作用域（Local）2.2 闭包作用域（Enclos
阅读更多...
Python实现对阿里云OSS对象存储的操作详解

Python实现对阿里云OSS对象存储的操作详解

《Python实现对阿里云OSS对象存储的操作详解》这篇文章主要为大家详细介绍了Python实现对阿里云OSS对象存储的操作相关知识,包括连接,上传,下载,列举等功能,感兴趣的小伙伴可以了解下... 目录一、直接使用代码二、详细使用1. 环境准备2. 初始化配置3. bucket配置创建4. 文件上传到os
阅读更多...
MySQL查询JSON数组字段包含特定字符串的方法

MySQL查询JSON数组字段包含特定字符串的方法

《MySQL查询JSON数组字段包含特定字符串的方法》在MySQL数据库中,当某个字段存储的是JSON数组,需要查询数组中包含特定字符串的记录时传统的LIKE语句无法直接使用,下面小编就为大家介绍两种... 目录问题背景解决方案对比1. 精确匹配方案（推荐）2. 模糊匹配方案参数化查询示例使用场景建议性能优
阅读更多...
关于集合与数组转换实现方法

关于集合与数组转换实现方法

《关于集合与数组转换实现方法》：本文主要介绍关于集合与数组转换实现方法,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地方,望不吝赐教... 目录1、Arrays.asList()1.1、方法作用1.2、内部实现1.3、修改元素的影响1.4、注意事项2、list.toArray()2.1、方
阅读更多...
Java中的雪花算法Snowflake解析与实践技巧

Java中的雪花算法Snowflake解析与实践技巧

《Java中的雪花算法Snowflake解析与实践技巧》本文解析了雪花算法的原理、Java实现及生产实践,涵盖ID结构、位运算技巧、时钟回拨处理、WorkerId分配等关键点,并探讨了百度UidGen... 目录一、雪花算法核心原理1.1 算法起源1.2 ID结构详解1.3 核心特性二、Java实现解析2.
阅读更多...
使用Python实现可恢复式多线程下载器

使用Python实现可恢复式多线程下载器

《使用Python实现可恢复式多线程下载器》在数字时代,大文件下载已成为日常操作,本文将手把手教你用Python打造专业级下载器,实现断点续传,多线程加速,速度限制等功能,感兴趣的小伙伴可以了解下... 目录一、智能续传：从崩溃边缘抢救进度二、多线程加速：榨干网络带宽三、速度控制：做网络的好邻居四、终端交互
阅读更多...
MySQL count()聚合函数详解

MySQL count()聚合函数详解

《MySQLcount()聚合函数详解》MySQL中的COUNT()函数,它是SQL中最常用的聚合函数之一,用于计算表中符合特定条件的行数,本文给大家介绍MySQLcount()聚合函数,感兴趣的朋... 目录核心功能语法形式重要特性与行为如何选择使用哪种形式？总结深入剖析一下 mysql 中的 COUNT
阅读更多...
java实现docker镜像上传到harbor仓库的方式

java实现docker镜像上传到harbor仓库的方式

《java实现docker镜像上传到harbor仓库的方式》：本文主要介绍java实现docker镜像上传到harbor仓库的方式,具有很好的参考价值,希望对大家有所帮助,如有错误或未考虑完全的地... 目录1. 前 言2. 编写工具类2.1 引入依赖包2.2 使用当前服务器的docker环境推送镜像2.2
阅读更多...
C++20管道运算符的实现示例

C++20管道运算符的实现示例

《C++20管道运算符的实现示例》本文简要介绍C++20管道运算符的使用与实现,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的朋友们下面随着小编来一起学习学习吧... 目录标准库的管道运算符使用自己实现类似的管道运算符我们不打算介绍太多，因为它实际属于c++20最为重要的
阅读更多...
Java easyExcel实现导入多sheet的Excel

Java easyExcel实现导入多sheet的Excel

《JavaeasyExcel实现导入多sheet的Excel》这篇文章主要为大家详细介绍了如何使用JavaeasyExcel实现导入多sheet的Excel,文中的示例代码讲解详细,感兴趣的小伙伴可... 目录1.官网2.Excel样式3.代码1.官网easyExcel官网2.Excel样式3.代码
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2