本文主要是介绍Pure Mathematics 4-Differentiation(微分),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
5.1 Parametric differentiation
Prior knowledge(预备知识)

P4的课本提到预备知识是P1的4.1和4.3
①P1的4.1和4.3里面其实没有引入 t t t参数。只讲了函数曲线和坐标轴交点(coordinate axes)。
②此处Prior knowledge直接出现了 x = f ( t ) = 3 t 2 − 5 t x=f(t)=3t^2-5t x=f(t)=3t2−5t形式
这就很尴尬了,明明没有学过含有t的参数方程,却放到预备知识里面说已经学过了。
综合①②,课本承认引入了t轴(也就是第三个坐标轴)
参数方程-引言
下图到底是什么?圆?正方形?

其实是一个 曲面构成的圆柱体。
我们上小学 时几何是怎么学习?
一、学习一个圆规,去画一个圆
二、学习一把尺子,去画一个正方形
正方形、矩形有四条边,比圆复杂很多很多。
三、老师拿出一个易拉罐,侧面是矩形,俯视时是圆形。
上述举例即是参数方程的核心思想-已知两个投影面信息,求第三个投影面的信息(例如微分)。
下面我们来看一道题,体会参数方程的含义。
根据 讲课 需要,我们先讲Example2,再讲Example1
Example2
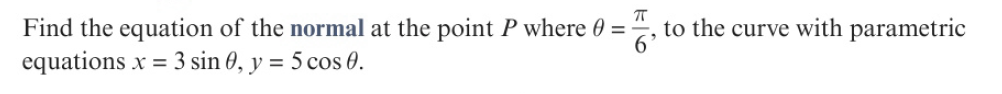
d x d θ = 3 cos θ , d y d θ = − 5 sin θ 0 ≤ θ < 2 π d y d x = − 5 sin θ 3 cos θ At p o i n t P , w h e r e θ = π 6 d y d x = − 5 × 1 2 3 × 3 2 = − 5 3 3 \begin{aligned} &\frac{dx}{d\theta}=3\cos\theta,\frac{dy}{d\theta}=-5\sin\theta\quad0\leq\theta<2\pi \\ & \frac{dy}{dx}=\frac{-5\sin\theta}{3\cos\theta} \\ &\text{At} \mathrm{point~}P,\mathrm{~where~}\theta=\frac\pi6 \\ &\frac{dy}{dx}=\frac{-5\times\frac12}{3\times\frac{\sqrt3}2}=\frac{-5}{3\sqrt3} \end{aligned} dθdx=3cosθ,dθdy=−5sinθ0≤θ<2πdxdy=3cosθ−5sinθAtpoint P, where θ=6πdxdy=3×23−5×21=33−5
课堂提问:tangent多少?
tangent·normal=-1
The gradient of the normal at P i s 3 3 5 and at P , x = 3 2 , y = 5 3 2 The equation of the normal is y − 5 3 2 = 3 3 5 ( x − 3 2 ) ⋅ ∴ 5 y = 3 3 x + 8 3 \begin{aligned} &\text{The gradient of the normal at }P\mathrm{~is~}\frac{3\sqrt{3}}5 \\ &\text{and at }P,x=\frac{3}{2},y=\frac{5\sqrt{3}}{2} \\ &\text{The equation of the normal is} \\ &y-\frac{5\sqrt{3}}{2}=\frac{3\sqrt{3}}{5}\left(x-\frac{3}{2}\right)\cdot \\ &\therefore5y=3\sqrt{3}x+8\sqrt{3} \end{aligned} The gradient of the normal at P is 533and at P,x=23,y=253The equation of the normal isy−253=533(x−23)⋅∴5y=33x+83
(授课时运行三维图观看,代码如下)
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的b问题# 参数θ的取值范围和精度
thetas = np.linspace(0, 2 * np.pi, 100) # 参数方程
x = 3 * np.sin(thetas)
y = 5 * np.cos(thetas) # 创建一个3D图形
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d') # 绘制曲线
ax.plot(x, y, thetas, label='参数方程')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('θ')
ax.legend() # 显示图形
plt.show()
Example2投影图汇总
| 投影方向 | 投影图 |
|---|---|
| y y y方向投影(俯视) x = 3 s i n θ x=3sin\theta x=3sinθ | 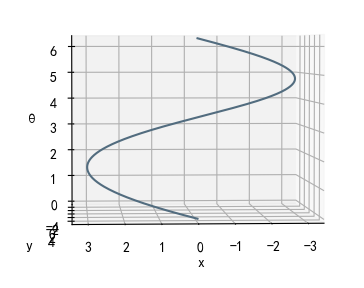 |
| x x x方向投影(俯视) y = 5 c o s θ y=5cos\theta y=5cosθ | 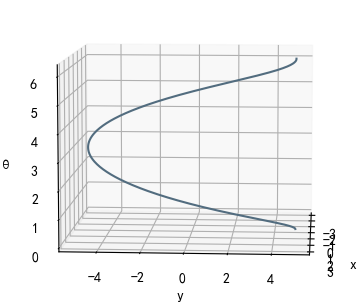 |
| θ \theta θ方向投影(俯视) x 2 9 + y 2 25 = 1 \frac{x^2}{9}+\frac{y^2}{25}=1 9x2+25y2=1 | 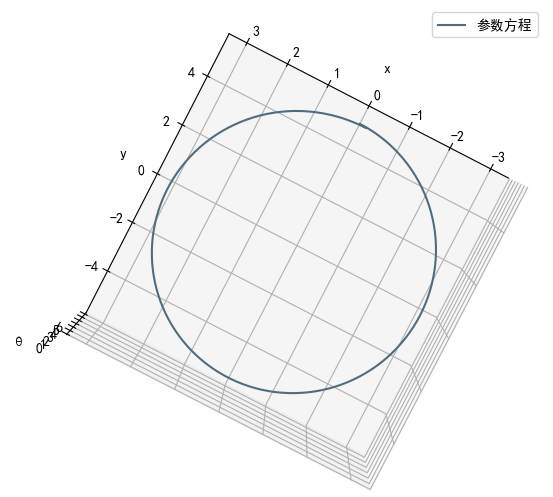 |
| 三维视图 | 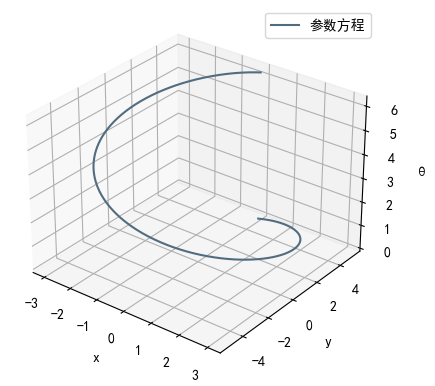 |
有些同学是在高中阶段才学过椭圆,其实根据上面的Python代码绘制,
我们看到,参数方程其实是一个螺旋上升的曲线。
那么螺旋上升的曲线有什么用呢?难道只是为了应付考试吗?
Parametric Equation在天体物理学中的应用
太阳系的螺旋运动
例如,在视频1:55我们看到侧面图
地球绕太阳转的轨迹是一个三角函数(正余弦取决于y轴的位置,y轴往右移动 π 2 \frac{\pi}{2} 2π就会变成cosine函数)
| 视角 | 图像 |
|---|---|
| x、y方向投影 (视频1:55) | 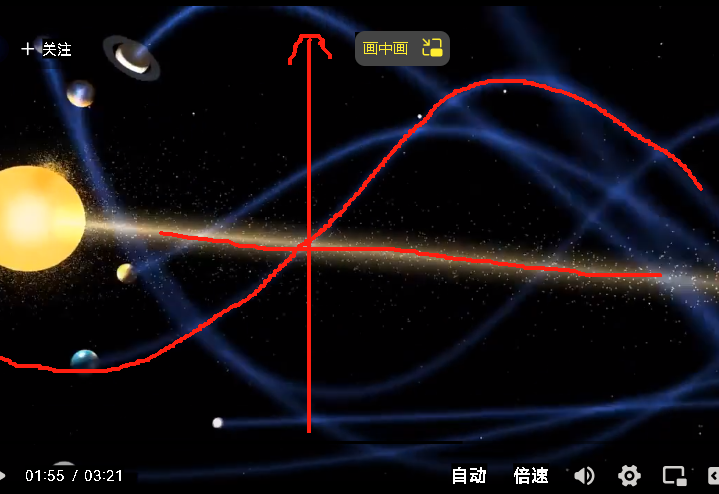 |
| θ \theta θ方向投影 一个椭圆轨迹 (视频0:13) |  |
| 三维视角 视频2:46之后 地球围绕太阳螺旋上升 |  |
上面是Parametric Equation在天体物理学中的应用。
这个题目到底在讲什么?
其实是一个三维空间中,螺旋上升的曲线,通过参数方程*来表达。
已知两个投影面(正弦、余弦)的微分,求 第三个面(投影图案是椭圆)的微分。
如何求呢?链式法则。
所以什么是参数方程?
看见参数方程,马上想到易拉罐。
一个易拉罐就是参数方程。
什么是易拉罐?
你从不同的方向来看,都会看到不同的图形。
俗话说:
横看成岭侧成峰,
远近高低进不同。
这就是参数方程
根据上述图示,链式法则的几何意义是什么?
链式法则几何意义:
一、
已知y-t微分关系
已知x-t微分关系
求y和x微分
d y d x = d y d t d x d t \frac{dy}{dx}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}} dxdy=dtdxdtdy
二、
已知两个投影面(x-θ、y-θ)的曲线斜率,求第三个投影面(x-y)曲线斜率
d y d x = f ′ ( x ) = y t ′ x t ′ \frac{dy}{dx}=f'(x)=\frac{y_t'}{x_t'} dxdy=f′(x)=xt′yt′
知识点总结
几何意义(不做考试要求,只是为了便于理解、记忆)。
链式法则(已知两个微分,求另一个微分)
切线(tangent)
法线(normal)
Example1
代码实现
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的b问题# 参数θ的取值范围和精度
t = np.linspace(0, 2 * np.pi, 400) # 参数方程
# x = 3 * np.sin(thetas)
# y = 5 * np.cos(thetas) x=t**3+t
y=t**2+1 # 创建一个3D图形
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d') # 绘制曲线
ax.plot(x, y, t, label='参数方程')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('t')
ax.legend() # 显示图形
plt.show()
运行结果
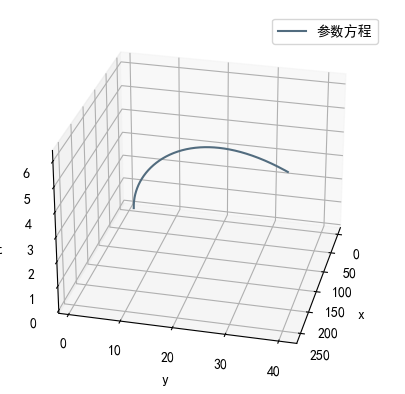
5.2 Implicit differentiation
概念回顾
| 概念 | 表示举例 |
|---|---|
| 导数(derivative) | f’(x) |
| 微分(differentiation) | d y d x \frac{dy}{dx} dxdy、 f ( y ) d y \frac{f(y)}{dy} dyf(y) |
概念上,导数不能完全等同于微分,那么这和我们的考试有什么关系呢?
举例一:
①AB⊥BC,所以∠ABC是90°(这个说法是错的)
正确表述是:∠ABC是90°的角
举例二:
find tan∠BAC of the following triangle
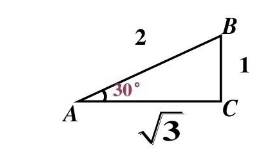
Wrong Solution:
B C A C = 1 3 \frac{BC}{AC}=\frac{1}{\sqrt{3}} ACBC=31
Right Solution:
t a n ∠ B A C = 1 3 tan∠BAC=\frac{1}{\sqrt{3}} tan∠BAC=31
为什么第一个回答是错的,第二个回答才是对的?
因为尽管 t a n ∠ B A C = B C A C tan∠BAC=\frac{BC}{AC} tan∠BAC=ACBC,但是题目要求的是tan∠BAC,所以不能直接写一个 B C A C 作为答案 \frac{BC}{AC}作为答案 ACBC作为答案
举例三
let y = x 2 , f i n d y=x^2,find y=x2,find d y d x \frac{dy}{dx} dxdy
Wrong Solution(错误回答):
f ′ ( x ) = 2 x f'(x)=2x f′(x)=2x
Right Solution:
d y d x = 2 x \frac{dy}{dx}=2x dxdy=2x
Right Solution:
d y d x = f ′ ( x ) = 2 x \frac{dy}{dx}=f'(x)=2x dxdy=f′(x)=2x
为什么第一个回答是错的,第二、三个回答是对的?
尽管 d y d x = f ′ ( x ) \frac{dy}{dx}=f'(x) dxdy=f′(x),但是题目要求的是 d y d x \frac{dy}{dx} dxdy,所以不能直接写一个f’(x)作为答案。
且在答题时候,如果涉及文字表述需要,应尽量使用differentiation,而不是 derivative
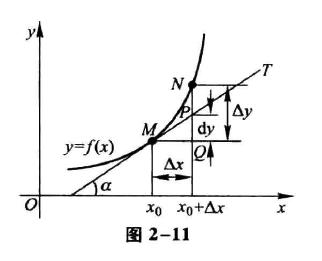
如图所示,尽管TM的斜率f’(x)= d y d x ( 图中 △ x = d x ) \frac{dy}{dx}(图中\triangle x=dx) dxdy(图中△x=dx)
概念上不是一个东西,题目问 d y d x 时,不要以 f ‘ ( x ) 开始来写 \frac{dy}{dx}时,不要 以f‘(x)开始 来写 dxdy时,不要以f‘(x)开始来写
学习目标
定理一、
d f ( y ) d x = f ′ ( y ) d y d x \frac{df(y)}{dx}=f'(y)\frac{dy}{dx} dxdf(y)=f′(y)dxdy
这个式子看起来不太友善。
分析:
f ′ ( y ) = d f ( y ) d y f'(y)=\frac{df(y)}{dy} f′(y)=dydf(y)
d ( f ( y ) ) d x = d f ( y ) d y ⋅ d y d x (链式法则) = f ′ ( y ) d y d x \frac{d(f(y))}{dx}=\frac{df(y)}{dy}·\frac{dy}{dx}(链式法则)=f'(y)\frac{dy}{dx} dxd(f(y))=dydf(y)⋅dxdy(链式法则)=f′(y)dxdy
所以与前面学过的 最大的不同,是 分子对y求微分,而不是对x求微分。这个不要搞混。尝试比较下面两个式子:
d y d x = d f ( x ) d x = f ′ ( x ) ( 这个式子在前面很常用 ) d f ( y ) d x = f ′ ( y ) d y d x ( 今天新学的,注意与上面一个区分开 ) \begin{aligned} \frac{dy}{dx}=\\ \frac{df(x)}{dx}&=f'(x)(这个式子在前面很常用)\\ \frac{df(y)}{dx}&=f'(y)\frac{dy}{dx}(今天新学的,注意与上面一个区分开) \end{aligned} dxdy=dxdf(x)dxdf(y)=f′(x)(这个式子在前面很常用)=f′(y)dxdy(今天新学的,注意与上面一个区分开)
定理二、
d ( x m y n ) d x = d ( x m ) d x y n + x m d ( y n ) d x = m x m − 1 y n + x m n y n − 1 d y d x \frac{d{(x^my^n)}}{dx}=\frac{d(x^m)}{dx}y^n+x^m\frac{d(y^n)}{dx}=mx^{m-1}y^n+x^mny^{n-1}\frac{dy}{dx} dxd(xmyn)=dxd(xm)yn+xmdxd(yn)=mxm−1yn+xmnyn−1dxdy
定理二推论:
1)当m=0,n≠0时
d ( x m y n ) d x = d ( y n ) d x = n y n − 1 d y d x \frac{d{(x^my^n)}}{dx}=\frac{d{(y^n)}}{dx}=ny^{n-1}\frac{dy}{dx} dxd(xmyn)=dxd(yn)=nyn−1dxdy
2)当m≠0,n=0时
d ( x m y n ) d x = d ( x m ) d x = m x m − 1 \frac{d{(x^my^n)}}{dx}=\frac{d{(x^m)}}{dx}=mx^{m-1} dxd(xmyn)=dxd(xm)=mxm−1
Example 3
Find d y d x in terms of x and y where x 3 + x + y 3 + 3 y = 6 \text{Find}\frac{\mathrm{d}y}{\mathrm{d}x}\text{in terms of}x\text{ and }y\text{ where }x^3+x+y^3+3y=6 Finddxdyin terms ofx and y where x3+x+y3+3y=6
3 x 2 + 1 + 3 y 2 d y d x + 3 d y d x = 0 d y d x ( 3 y 2 + 3 ) d y d x = − 3 x 2 − 1 3 ( 1 + y 2 ) \begin{aligned} 3x^{2}+1+3y^{2}{\frac{dy}{dx}}+3{\frac{dy}{dx}}& =0 \\ \\ \frac{dy}{dx}(3y^{2}+3) \frac{dy}{dx} & =-\frac{3x^2-1}{3(1+y^2)} \end{aligned} 3x2+1+3y2dxdy+3dxdydxdy(3y2+3)dxdy=0=−3(1+y2)3x2−1
结论:
一、看见x,直接对x求微分
二、看见y,直接对y求微分,再乘以x求微分
三、不推荐计算中使用乘号X,建议使用·,乘号X与变量x在考试时容易混淆。
记住上面的尤其第二条结论,我们来看下一题
Example 4(这道题的难点是xy乘在一起)
Given that 4 x y 2 + 6 x 2 y = 10 ,find the value of d y d x at the point ( 1 , 1 ) . \text{Given that }4xy^2+\frac{6x^2}{y}=10\text{,find the value of}\frac{\mathrm{d}y}{\mathrm{d}x}\text{at the point}(1,1). Given that 4xy2+y6x2=10,find the value ofdxdyat the point(1,1).
For this example, we can use the formula:
d ( u v ) d x = d u d x v + u d v d x ① \frac{d(uv)}{dx}=\frac{du}{dx}v+u\frac{dv}{dx}① dxd(uv)=dxduv+udxdv①(prior knowledge)
with the new formula we just learned:
d ( y n ) d x = n y n − 1 d y d x \frac{d{(y^n)}}{dx}=ny^{n-1}\frac{dy}{dx} dxd(yn)=nyn−1dxdy②(今天新学的)
d ( x m ) d x = m x m − 1 \frac{d(x^m)}{dx}=mx^{m-1} dxd(xm)=mxm−1③
关于①提问(uv拆分方式):
1)我能不能把 4 x y 2 4xy^2 4xy2拆成 u = 4 x y , v = y u=4xy,v=y u=4xy,v=y,即 u v = 4 x y 2 uv=4xy^2 uv=4xy2为什么?
2)我能不能把 4 x y 2 4xy^2 4xy2拆成 u = 2 x , v = 2 y 2 u=2x,v=2y^2 u=2x,v=2y2,即 u v = 4 x y 2 uv=4xy^2 uv=4xy2为什么?
3)我能不能把 4 x y 2 4xy^2 4xy2拆成 u = 4 x , v = y 2 u=4x,v=y^2 u=4x,v=y2,即 u v = 4 x y 2 uv=4xy^2 uv=4xy2为什么?(☆☆☆)
4)我能不能把 4 x y 2 4xy^2 4xy2拆成 u = x , v = 4 y 2 u=x,v=4y^2 u=x,v=4y2,即 u v = 4 x y 2 uv=4xy^2 uv=4xy2为什么?
1)的拆分方式会导致 u需要同时对x和y求导。
2)的拆分方式会导致考试时,求微分前就要同时照顾两个系数,增加计算量、检查工作量。
3)的拆分方式最佳,求微分前只关注1个 系数,求微分后才关注2个系数。
4)的拆分方式不建议,把x前的系数4给 y 2 y^2 y2,不方便校对
uv拆分建议(考试时拆分uv的原则):
1)系数给最近的因子
2)u或v尽量只包含一个字母
3)u中只包含x,v中只包含y
举例 8 e 2 y x 3 8e^{2y}x^3 8e2yx3拆分成uv形式是多少?
推荐
u = x 3 u=x^3 u=x3
v = 8 e 2 y v=8e^{2y} v=8e2y
重写①式有:
d ( u v ) d x = d u d x v + u d v d y d y d x ④ \frac{d(uv)}{dx}=\frac{du}{dx}v+u\frac{dv}{dy}\frac{dy}{dx}④ dxd(uv)=dxduv+udydvdxdy④
对比之前学过的内容有
| u , v u,v u,v情况 | u v uv uv的微分形式 |
|---|---|
| u u u, v v v中都不含 y y y | d ( u v ) d x = d u d x v + u d v d x \frac{d(uv)}{dx}=\frac{du}{dx}v+u\frac{dv}{dx} dxd(uv)=dxduv+udxdv |
| u u u不含 y y y, v v v含 y y y | d ( u v ) d x = d u d x v + u d v d y d y d x \frac{d(uv)}{dx}=\frac{du}{dx}v+u\frac{dv}{dy}\frac{dy}{dx} dxd(uv)=dxduv+udydvdxdy |
| u u u含 y y y, v v v不含 y y y | d ( u v ) d x = d u d y d y d x v + u d v d x \frac{d(uv)}{dx}=\frac{du}{dy}\frac{dy}{dx}v+u\frac{dv}{dx} dxd(uv)=dydudxdyv+udxdv |
| u u u含 y y y, v v v含 y y y | d ( u v ) d x = d u d y d y d x v + u d v d y d y d x \frac{d(uv)}{dx}=\frac{du}{dy}\frac{dy}{dx}v+u\frac{dv}{dy}\frac{dy}{dx} dxd(uv)=dydudxdyv+udydvdxdy |
为什么会有这样的 规律 ?
因为y和x是相关的,所以求 微分的时候需要做到“遍历”
如果y和x是不相关的,那么求微分的 时候,直接为零。
所谓的相关性,其实用生活中的话来说:是否搭嘎,例如 两人不搭噶
因为y的表达式中包含有x,所以y和x是搭嘎的,所以看见 y的时候,不能 当作没看见,
需要先计算 d f ( y ) d y \frac{df(y)}{dy} dydf(y)(这里的 f ( y ) f(y) f(y)可以是u也可以是v,再计算 d y d x \frac{dy}{dx} dxdy
相关性的概念会在后面的概率论与数理统计中慧提到。
The original equation can be rearranged as(根据上述流程图来计算):
4 x ⋅ y 2 + 6 x 2 1 y = 10 4x·y^2+6x^2\frac{1}{y}=10 4x⋅y2+6x2y1=10
Let u = 4 x u=4x u=4x, v = y 2 v=y^2 v=y2
d ( u v ) d x = d u d x v + u d v d y d y d x \frac{d(uv)}{dx}=\frac{du}{dx}v+u\frac{dv}{dy}\frac{dy}{dx} dxd(uv)=dxduv+udydvdxdy
( 4 y 2 + 4 x ⋅ 2 y d y d x ) + ( 12 x y − 6 x 2 y 2 d y d x ) = 0 Substitute x=1, y=1 to give. ( 8 d y d x + 4 ) + ( 12 − 6 d y d x ) = 0 16 + 2 d y d x = 0 d y d x = − 8 \begin{aligned} &&\left(4y^{2}+4x · 2y\frac{dy}{dx}\right)+\left(\frac{12x}{y}-\frac{6x^{2}}{y^{2}}\frac{dy}{dx}\right)&=0 \\ &&\text{Substitute x=1, y=1 to give.} \\ &&\left(8\frac{dy}{dx}+4\right)+\left(12-6\frac{dy}{dx}\right)=0 \\ &&16+2\frac{dy}{dx} =0 \\ &&\frac{\mathrm{d}y}{\mathrm{d}x} =-8 \end{aligned} (4y2+4x⋅2ydxdy)+(y12x−y26x2dxdy)Substitute x=1, y=1 to give.(8dxdy+4)+(12−6dxdy)=016+2dxdy=0dxdy=−8=0
Example5
Find the value of d y d x at the point ( 1 , 1 ) where e 2 x ln y = x + y − 2. \text{Find the value of}\frac{\mathrm{d}y}{\mathrm{d}x}\text{at the point}(1,1)\text{where e}^{2x}\ln y=x+y-2. Find the value ofdxdyat the point(1,1)where e2xlny=x+y−2.
e 2 x ⋅ 1 y d y d x + ln y ⋅ 2 e 2 x = 1 + d y d x Substitute x=1, y=1 to give e 2 ⋅ d y d x = 1 + d y d x ∴ ( e 2 − 1 ) d y d x = 1 d y d x = 1 e 2 − 1 \begin{aligned} &e^{2x}·{\frac{1}{y}}{\frac{dy}{dx}}+\ln y ·2e^{2x}=1+{\frac{dy}{dx}} \\ &\text{Substitute x=1, y=1 to give} \\ &&e^{2}·\frac{dy}{dx}=1+\frac{dy}{dx} \\ &\therefore\quad(e^2-1)\frac{dy}{dx}=1 \\ &&\frac{\mathrm{d}y}{\mathrm{d}x} =\frac1{e^2-1} \end{aligned} e2x⋅y1dxdy+lny⋅2e2x=1+dxdySubstitute x=1, y=1 to give∴(e2−1)dxdy=1e2⋅dxdy=1+dxdydxdy=e2−11
Example6
Given that the area of a circle A cm 2 is related to its radius r cm by the formula A = π r 2 , and that the rate of change of its radius in cms − 1 is given by d r d t = 5 , find d A d t when r = 3 \begin{array}{l}\text{Given that the area of a circle }A\text{cm}^2\\ \text{is related to its radius}r\text{cm by the formula}A=\pi r^2,\\ \text{and that}\text{the rate of change of its radius in cms}^{-1}\text{is given by}\frac{\mathrm{d}r}{\mathrm{d}t}=5,\text{find}\\ \frac{\mathrm{d}A}{\mathrm{d}t}\text{when}r=3\end{array} Given that the area of a circle Acm2is related to its radiusrcm by the formulaA=πr2,and thatthe rate of change of its radius in cms−1is given bydtdr=5,finddtdAwhenr=3
A = π r 2 ∴ d A d r = 2 π r U s i n g d A d t = d A d r ⋅ d r d t d A d t = 2 π r ⋅ 5 = 30 π , w h e n r = 3 \begin{aligned} \text{A}& =\pi r^2 \\ \therefore\frac{dA}{dr}& =2\pi r \\ \mathrm{Using~}\frac{\mathrm{d}A}{\mathrm{d}t}& =\frac{dA}{dr}·\frac{dr}{dt} \\ \frac{\mathrm{d}A}{\mathrm{d}t}& =2\pi r ·5 \\ &=30\pi,\mathrm{~when~}r=3 \end{aligned} A∴drdAUsing dtdAdtdA=πr2=2πr=drdA⋅dtdr=2πr⋅5=30π, when r=3
Example7
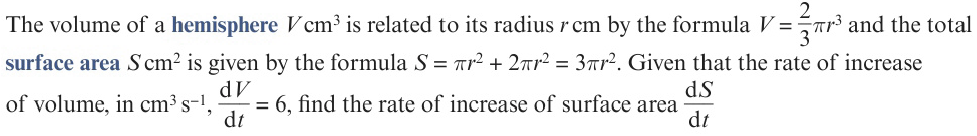
思路解析:
题目中有S=r的相关表达式,所以可以推出 d S d r \frac{dS}{dr} drdS
题目中有V=r的相关表达式,所以可以推出 d V d r \frac{dV}{dr} drdV
题目中有 d V d t \frac{dV}{dt} dtdV
求 d S d t \frac{dS}{dt} dtdS
通过链式法则进行尝试拼凑
Solution:
V = 2 3 π r 3 and S = 3 π r 2 - d V d r = 2 π r 2 and d S d r = 6 π r \begin{aligned}V&=\frac{2}{3}\pi r^3\text{and}S=3\pi r^2\textbf{-}\\\frac{dV}{dr}&=2\pi r^2\text{and}\frac{dS}{dr}=6\pi r\end{aligned} VdrdV=32πr3andS=3πr2-=2πr2anddrdS=6πr
N o w d S d t = d S d r ⋅ d r d V ⋅ d V d t = 6 π r ⋅ s 1 2 π r 2 ⋅ 6 = 18 r \begin{aligned} \mathrm{Now}\frac{\mathrm{d}S}{\mathrm{d}t}& =\frac{dS}{dr}·\frac{dr}{dV}·\frac{dV}{dt} \\ &=6\pi r·s\frac1{2\pi r^2}·6 \\ &=\frac{18}r \end{aligned} NowdtdS=drdS⋅dVdr⋅dtdV=6πr⋅s2πr21⋅6=r18
Example8
In the decay of radioactive particles(放射性粒子),the rate at which particles decay is proportional to the number of particles remaining Write down a differential equation for the rate of change of the number of particles.
Let N N N be the number of particles and let t be time.
The rate of change of the number of particles d N d t \frac{dN}{dt} dtdN is proportional to N N N.i.e.(也就是,即。源自拉丁文id est,读作 that is) d N d t = − k N \frac{dN}{dt}=-kN dtdN=−kN,
where k k k is a positive constant.The minus sign(负号) arises because the number of particles is decreasing.
Example9
Newton’s law of cooling states that the rate of loss of temperature of a body is proportional to the excess temperature of the body over its surroundings.Write an equation that expresses this law.
牛顿冷却定律:一个热的物体的冷却速度与该物体和周围环境的温度差成正比。
Let the temperature of the body be θ \theta θ degrees and the time be t t t seconds.
The rate of change of the temperature d θ d t \frac{d\theta}{dt} dtdθ is proportional to θ − θ 0 \theta-\theta_0 θ−θ0,where θ 0 \theta_0 θ0 is the temperature of the surroundings.
i.e. d θ d t = − k ( θ − θ 0 ) \frac{d\theta}{dt}=-k(\theta-\theta_0) dtdθ=−k(θ−θ0),where k k k is a positive constant.
Example10

Since V = 4 3 π R 3 . d V d R = 4 π R 2 ∴ d V d t = d V d R × d R d t = 4 π R 2 × d R d t B u t a s d V d t = − k A 4 π R 2 × d R d t = − k × 4 π R 2 ∴ d R d t = − k \begin{aligned} \text{Since V}& =\frac43\pi R^3. \\ \frac{\mathrm{d}V}{\mathrm{d}R}& =4\pi R^2 \\ \therefore\frac{\mathrm{d}V}{\mathrm{d}t}& =\frac{dV}{dR}\times\frac{dR}{dt}=4\pi R^2\times\frac{dR}{dt} \\ \mathrm{But~as}~\frac{\mathrm{d}V}{\mathrm{d}t}& =-kA \\ 4\pi R^2\times\frac{dR}{dt}& =-k\times4\pi R^{2} \\ ∴\frac{dR}{dt}& =-k \end{aligned} Since VdRdV∴dtdVBut as dtdV4πR2×dtdR∴dtdR=34πR3.=4πR2=dRdV×dtdR=4πR2×dtdR=−kA=−k×4πR2=−k
Challenge
重点讲下这道题
a.
d y d x = d y d t d t d x = 4 c o s 2 t ⋅ − 1 5 s i n ( t + π 12 ) = − 4 c o s 2 t 5 s i n ( t + p i 12 ) \frac{dy}{dx}=\frac{dy}{dt}\frac{dt}{dx}\\ =4cos2t·\frac{-1}{5sin(t+\frac{\pi}{12})}\\ =\frac{-4cos2t}{5sin(t+\frac{pi}{12})} dxdy=dtdydxdt=4cos2t⋅5sin(t+12π)−1=5sin(t+12pi)−4cos2t
b.
c o s 2 t = 0 cos2t=0 cos2t=0 and 5 s i n ( t + π 12 ) 5sin(t+\frac{\pi}{12}) 5sin(t+12π)≠0
t∈[0, 2 π 2\pi 2π]
2 t = π 2 + k π ∈ [ 0 , 4 π ] 2t=\frac{\pi}{2}+k\pi∈[0,4\pi] 2t=2π+kπ∈[0,4π]
k=0,1,2,3
we can get the following 4 points.
| k | t | coordinates( 5 c o s ( t + π 12 ) , 2 s i n 2 t 5cos(t+\frac{\pi}{12}),2sin2t 5cos(t+12π),2sin2t) |
|---|---|---|
| 0 | π 4 \frac{\pi}{4} 4π | (5 c o s π 3 , 2 ) cos\frac{\pi}{3},2) cos3π,2)=( 5 2 \frac{5}{2} 25,2) |
| 1 | 3 π 4 \frac{3\pi}{4} 43π | ( 5 c o s 5 π 6 5cos\frac{5\pi}{6} 5cos65π,-2)=( − 5 3 2 , − 2 -\frac{5\sqrt{3}}{2},-2 −253,−2) |
| 2 | 5 π 4 \frac{5\pi}{4} 45π | ( 5 c o s 4 π 3 (5cos\frac{4\pi}{3} (5cos34π,2)=( − 5 2 , 2 ) -\frac{5}{2},2) −25,2) |
| 3 | 7 π 4 \frac{7\pi}{4} 47π | 5 c o s ( 11 π 6 , − 2 ) = ( − 5 3 2 , − 2 ) 5cos(\frac{11\pi}{6},-2)=(\frac{-5\sqrt{3}}{2},-2) 5cos(611π,−2)=(2−53,−2) |
c
1)For y = 2 s i n 2 t = 0 y=2sin2t=0 y=2sin2t=0(x-axis)
∵ 2 t ∈ [ 0 , 4 π ] ∵2t∈[0,4\pi] ∵2t∈[0,4π]
∴ 2 t = k ⋅ π ∴2t=k·\pi ∴2t=k⋅π
∴ t = k π 2 ∴t=\frac{k\pi}{2} ∴t=2kπ
| k | 2t | points | d y d x = − 4 c o s 2 t 5 s i n ( t + p i 12 ) \frac{dy}{dx}=\frac{-4cos2t}{5sin(t+\frac{pi}{12})} dxdy=5sin(t+12pi)−4cos2t |
|---|---|---|---|
| 0 | 0 | ( 5 c o s π 12 5cos\frac{\pi}{12} 5cos12π,0)=(4.83.0) | -3.09 |
| 1 | π \pi π | ( 5 c o s 7 π 12 5cos\frac{7\pi}{12} 5cos127π,0)=(-1.29,0) | 0.828 |
| 2 | 2 π 2\pi 2π | ( 5 c o s 13 π 12 5cos\frac{13\pi}{12} 5cos1213π,0)=(-4.83,0) | 3.09 |
| 3 | 3 π 3\pi 3π | ( 5 c o s 19 π 12 5cos\frac{19\pi}{12} 5cos1219π,0)=(1.29,0) | -0.83 |
| 4 | 4 π 4\pi 4π | ( 5 c o s 25 π 12 5cos\frac{25\pi}{12} 5cos1225π,0)=(4.83.0) | -3.09 |
上述结果的python代码(考试时使用计算器)
import math
k=4
# 定义变量
t = k*math.pi/2 # 你可以根据需要更改这个值 points=5*math.cos(t+math.pi/12)
# 计算表达式
gradient = (-4 * math.cos(2 * t) / (5 * math.sin(t + math.pi / 12))) # 打印结果
print("points=",points)
print("gradient=",gradient)
2)For x = 5 c o s ( t + π 12 ) = 0 x=5cos(t+\frac{\pi}{12})=0 x=5cos(t+12π)=0(x-axis)
t + π 12 = 2 k + 1 2 π t+\frac{\pi}{12}=\frac{2k+1}{2}\pi t+12π=22k+1π
| k | t | points ( 5 c o s ( t + π 12 ) , 2 s i n 2 t ) (5cos(t+\frac{\pi}{12}),2sin2t) (5cos(t+12π),2sin2t) | d y d x = − 4 c o s 2 t 5 s i n ( t + p i 12 ) \frac{dy}{dx}=\frac{-4cos2t}{5sin(t+\frac{pi}{12})} dxdy=5sin(t+12pi)−4cos2t |
|---|---|---|---|
| 0 | 5 π 12 \frac{5\pi}{12} 125π | (0,1) | 0.693 |
| 1 | 17 π 12 \frac{17\pi}{12} 1217π | (0,1) | -0.693 |
python代码是
import math
k=1
# 定义变量
t = (2*k+1)/2*math.pi-math.pi/12 # 你可以根据需要更改这个值 # points=5*math.cos(t+math.pi/12)
# 计算表达式
gradient = (-4 * math.cos(2 * t) / (5 * math.sin(t + math.pi / 12))) # 打印结果
# print("points=",points)
print("gradient=",gradient)
d
d x d t = − 5 s i n ( t + π 12 ) \frac{dx}{dt}=-5sin(t+\frac{\pi}{12}) dtdx=−5sin(t+12π)
t + π 12 = k π t+\frac{\pi}{12}=k\pi t+12π=kπ
| k | t | points ( 5 c o s ( t + π 12 ) , 2 s i n 2 t ) (5cos(t+\frac{\pi}{12}),2sin2t) (5cos(t+12π),2sin2t) | d x d t = − 5 s i n ( t + π 12 ) \frac{dx}{dt}=-5sin(t+\frac{\pi}{12}) dtdx=−5sin(t+12π) |
|---|---|---|---|
| 1 | 11 π 12 \frac{11\pi}{12} 1211π | (-5,-1) | 0 |
| 2 | 23 π 12 \frac{23\pi}{12} 1223π | (5,-1) | 0 |
Python代码
import math
k=2
# 定义变量
t = k*math.pi-math.pi/12 # 你可以根据需要更改这个值
print("t=",t)
x=5*math.cos(t+math.pi/12)
y=2*math.sin(2*t)
print(y)
print("(%d,%f)" % (x, y))e(为了绘制清晰一些,这里使用python实现,考试时要根据自己在前面几个小问求出的点来绘制)
# -*- coding: utf-8 -*-
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体plt.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的b问题# 参数方程
t = np.linspace(0, 2 * np.pi, 1000) # t的范围在0到2π,1000个点
y = 2 * np.sin(2 * t)
x = 5 * np.cos(t + np.pi/12) # 绘制图形
plt.figure(figsize=(6, 6)) # 设置图形大小
plt.plot(x, y, label='参数方程 y=2sin(2t), x=5cos(t+π/12)') # 绘制图形
plt.xlabel('x') # x轴标签
plt.ylabel('y') # y轴标签
plt.title('参数方程 y=2sin(2t) 和 x=5cos(t+π/12)') # 图形标题
plt.legend() # 显示图例
plt.grid(True) # 显示网格线 # 绘制x轴和y轴
plt.axhline(y=0, color='black', linestyle='--') # 绘制y轴
plt.axvline(x=0, color='black', linestyle='--') # 绘制x轴 plt.show() # 显示图形
Run the above Python code ,we get
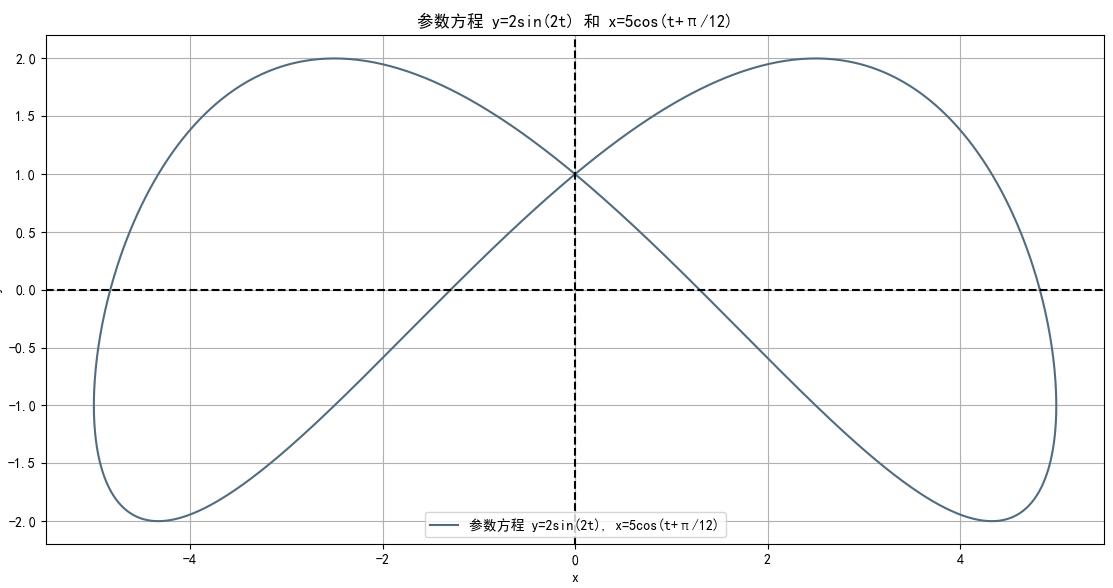
对同学们的要求
章节后面的E/P习题必须全部完成。
这篇关于Pure Mathematics 4-Differentiation(微分)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









