本文主要是介绍二叉搜索树,穷举(全排列),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
力扣230.二叉搜索树中第K小的元素
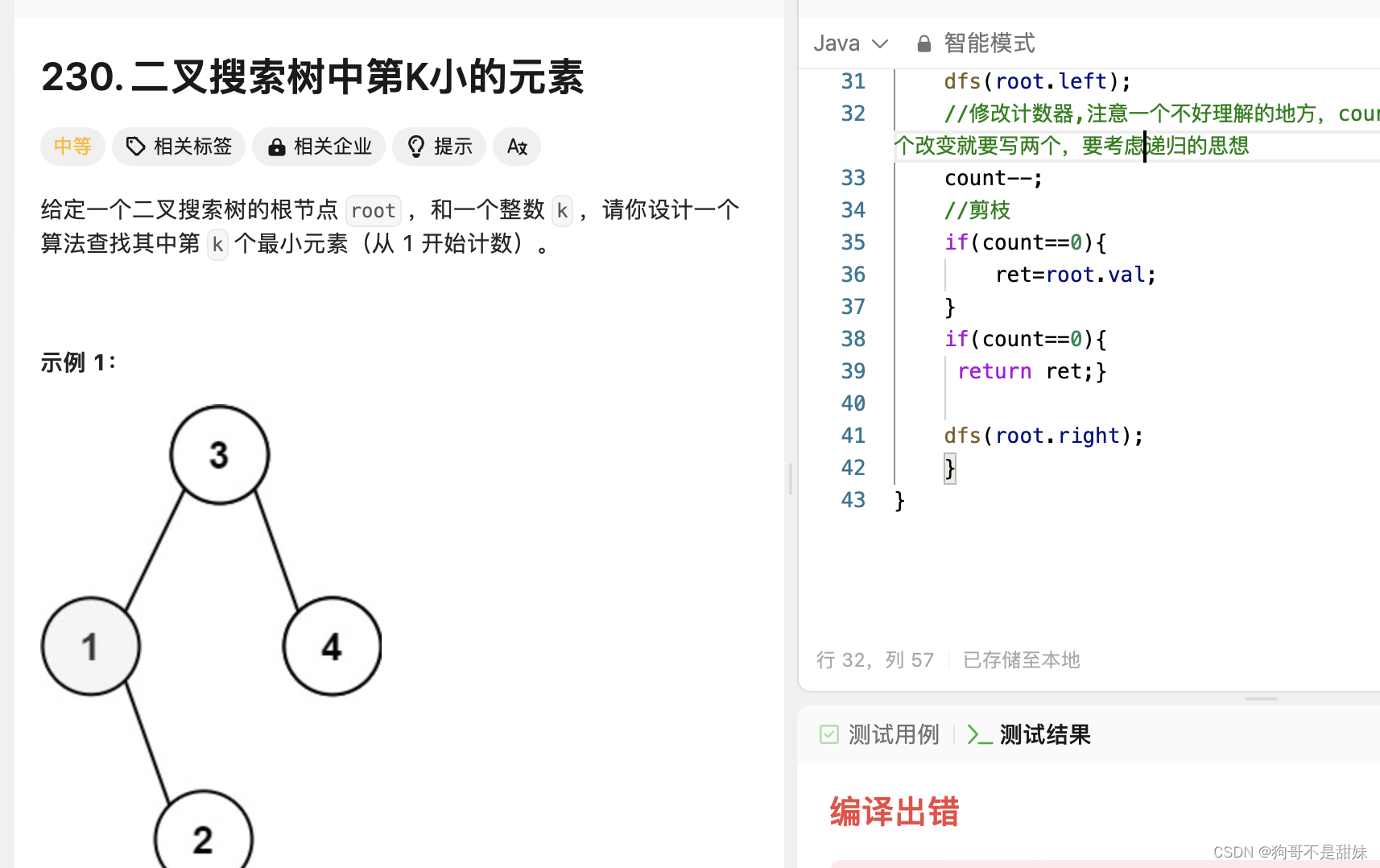
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/ class Solution {int count=Integer.MAX_VALUE;int ret=0;//可以尝试中序遍历,然后用数组去存储//两个全局变量,用中序遍历,然后再去计数public int kthSmallest(TreeNode root, int k) {count=k;dfs(root);return ret;}public void dfs(TreeNode root){//处理了剪枝的情况if(root==null||count==0){//提前退出的意思return ;}dfs(root.left);//修改计数器,注意一个不好理解的地方,count--写一个就够,他不是循环,两个改变就要写两个,要考虑递归的思想,我本人确实现在还没有那个思想,但是会慢慢努力count--;//剪枝if(count==0){ret=root.val;}if(count==0){return ;} //右子树重新递归的时候,会走那个count--,因为假如没有左子树,那么count 不变dfs(root.right);} }
力扣257.二叉树的所有路径
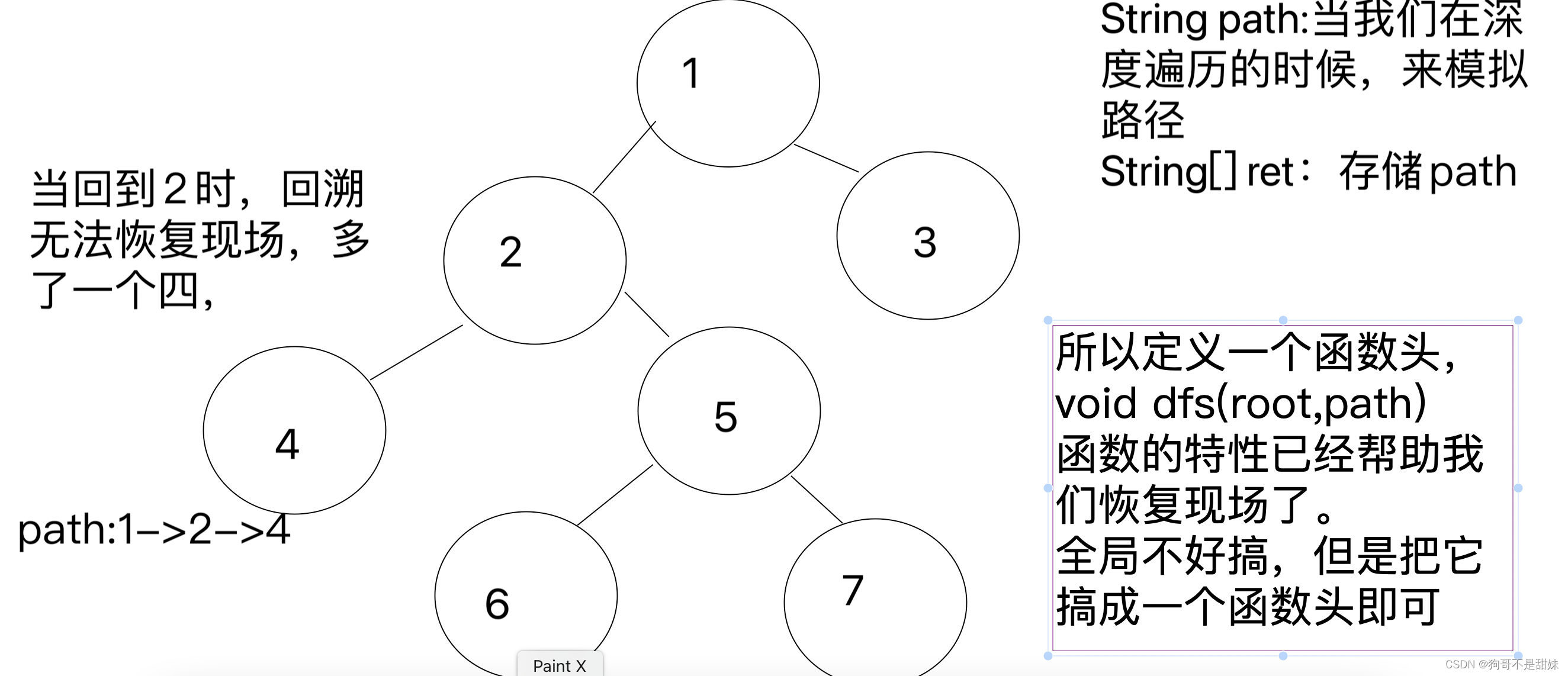
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/ class Solution {List <String>ret;public List<String> binaryTreePaths(TreeNode root) {dfs(root,new StringBuffer()); //传递的相当于是一个全局的StringBufferreturn ret;}//回溯:恢复现场,只要有递归,必然就有回溯,简单题中public void dfs(TreeNode root,StringBuffer _path){ //定义个变量,这样他回溯的时候,他不会影响那个_path,StringBuffer path=new StringBuffer(_path); //path加入root.val相当于保存当前节点的值path.append(Integer.toString(root.val));if(root.left==null&&root.right==null){ //到了叶子结点,那么路径的就基本已经出来了,所以要把他添加到ret里面,然后ret.add(path.toString());return;} //path加入这个->箭头,所有的修改都是在path这个地方修改path.append("->"); //这里传递的是path,而不是_path,因为_path已经存储了。而path没有存储,path还停留在根节点应该有的地方if(root.left!=null) dfs(root.left,path);if(root.right!=null)dfs(root.right,path);} }
回溯的用途就是递归后返回。剪枝的用途就是为了节省时间,如果某种情况不合格,就无须遍历其他节点。
力扣46.全排列

如果全部使用for循环会很难解决,所以选择使用递归。
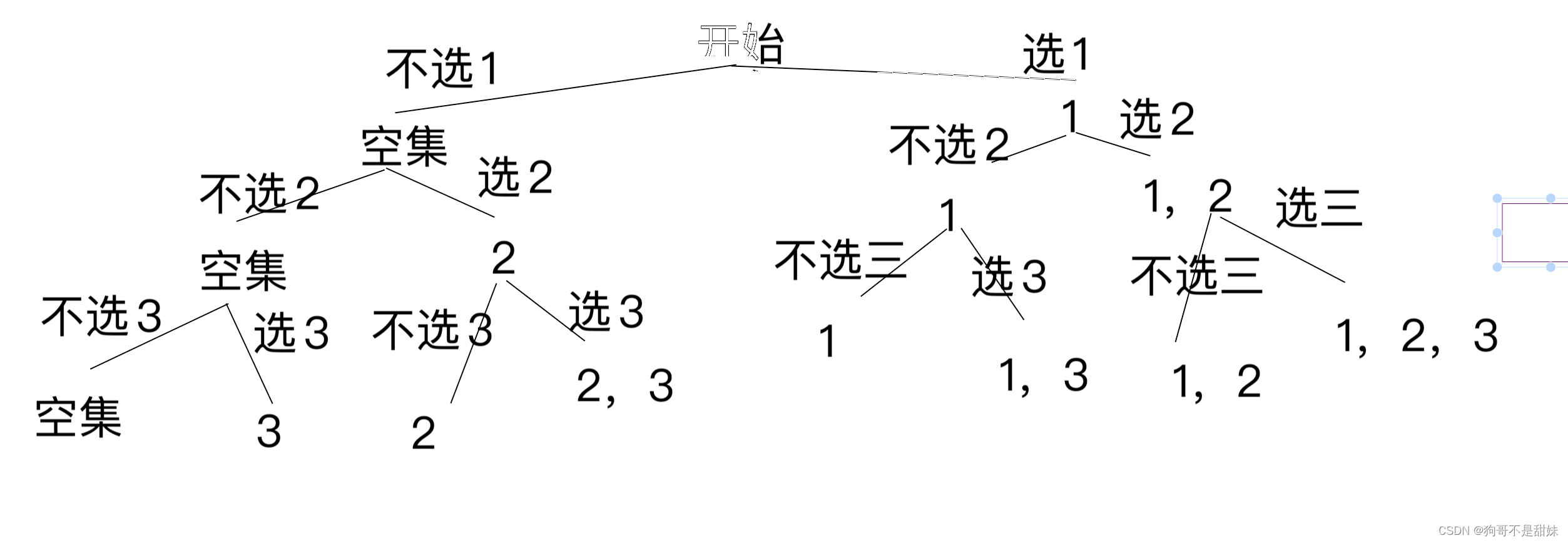
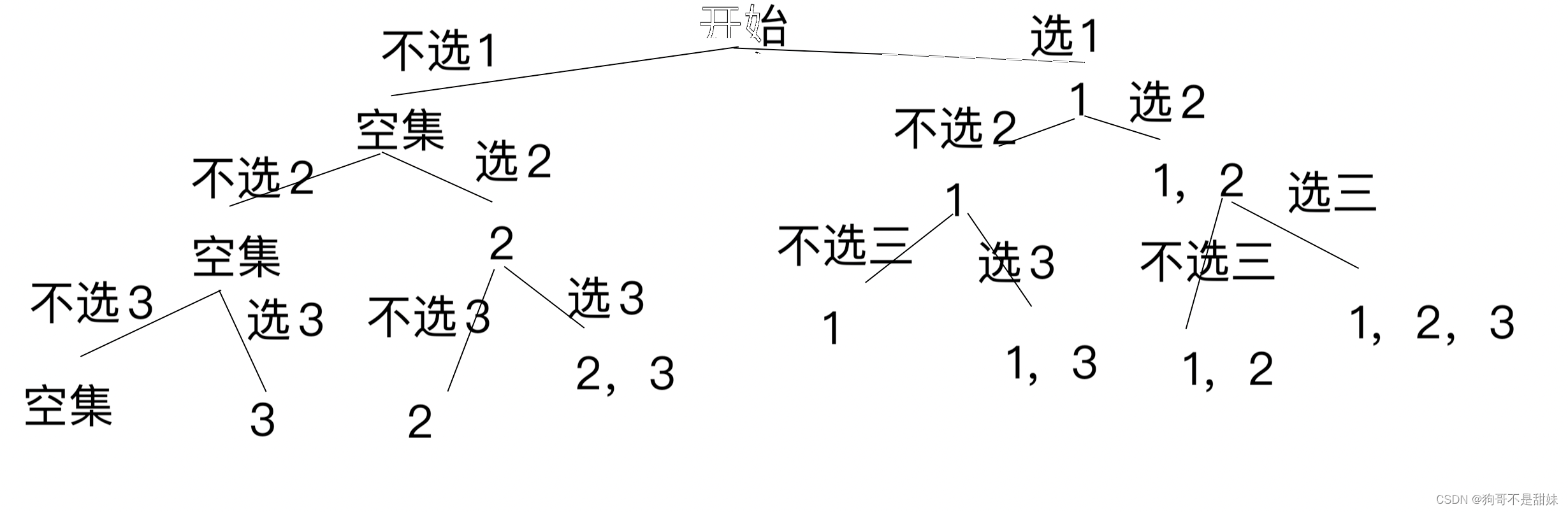
1.画出决策树,越详细越好(决策树:如何不从不漏的全部遍历一遍)
res.add(list)为浅拷贝,后续list内容的变化会导致res的变化,在原来地址改变数据,内容肯定会被改变res.add(new ArrayList(list))为深拷贝,对象中开辟一个新地址,存放的内容为list链表,所以后续不会被影响。
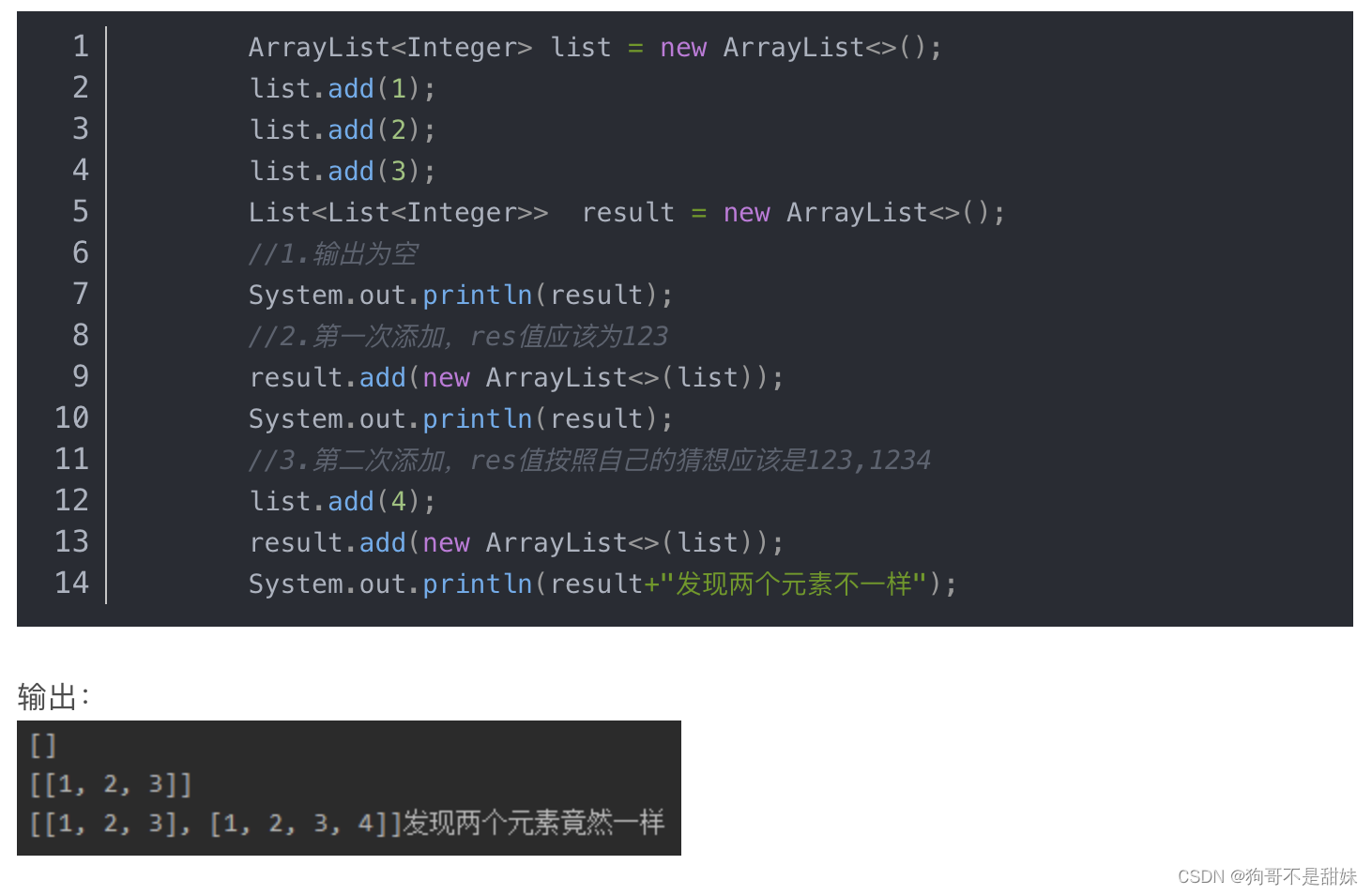
解释了什么是深拷贝,什么是浅拷贝
记住一件事,写算法,dfs不要套模版,套模版只会局限你的思维,这次我是很深的感受到,套代码这几个题,我都没有很好的思考出来。
class Solution {List<List<Integer>> ret=new ArrayList<>();List<Integer>path=new ArrayList<>();boolean[]check;public List<List<Integer>> permute(int[] nums) {check=new boolean[nums.length];
//这一步也不好想,为什么只穿一个数组,我刚开始是想传一个数组,再加上一个i,j,k标记到了第几个数字,我们只需判断path的长度是否等于nums的长度即可dfs(nums);return ret;}
public void dfs(int []nums){//出口if(path.size()==nums.length){//深拷贝,不影响path这个东西。ret.add(new ArrayList<>(path));return ;}for(int i=0;i<nums.length;i++){if(check[i]==false){//添加path.add(nums[i]);//标记一遍check[i]=true;//dfs进入下一层dfs(nums);//回溯->恢复现场 当dfs回来之后,把check恢复原来位置check[i]=false;//回溯减少一个,path.remove(path.size()-1);}}}
}力扣78.子集
步骤一:先画决策树
2.设计代码
全局变量
dfs()
细节问题

class Solution {List<List<Integer>>ret=new ArrayList<>();List<Integer>path=new ArrayList<>();public List<List<Integer>> subsets(int[] nums) {dfs(nums,0);return ret;}
//整个代码实现,我认为最难的部分在于怎么去写选和不选部分public void dfs(int[]nums,int i){if(i==nums.length){ret.add(new ArrayList<>(path));return;}//选,如果你要选,就要先添加,然后进入递归path.add(nums[i]);dfs(nums,i+1);// path.remove(nums[i+1]);
//这里去除也是细节,为神马不是上面那个去除,因为上面的去除,面临越界的事情,但是假如你是原有的path.remove就会去除下标为size-1这个位置的结果,因为他是数组。
path.remove(path.size()-1);//不选dfs(nums,i+1);}
}他是根据下标删除

解法2:我们for循环遍历的是下标

class Solution {List<List<Integer>>ret=new ArrayList<>();List<Integer>path=new ArrayList<>();
public List<List<Integer>> subsets(int[] nums) {dfs(nums,0);return ret;}
public void dfs(int[]nums,int pos){//这一步很细节,开始在想,他怎么才能是空,后来发现把path当成别的东西了,假如一开始添加他就,那他就是一个空的.ret.add(new ArrayList<>(path));//i=pos,这一步是为了让他到达pos的地方,也就是到达了第几层// 这个for表示的是让决策树横着走for(int i=pos;i<nums.length;i++){path.add(nums[i]);
//注意这里是i+1,还是pos+1,因为他的i从i的下一个位置开始依次枚举,假如是pos会出现什么结果呢,假如说是pos,当i从1变成2的时候pos是不改变的,换句话说,他还会再往下重复走一块,为什么是i+1,就是因为不让他重复走,这个dfs是表示让决策树往下走,假如是只有2的话,那个i=0,然后pos=1,ret加入这个2,此时i页=1,path又去加这个i,此时他就是22,然后再次进入,那么就ret 就进入了22,所以pos是不正确的,那么假如是i的话,就会往下递归正常的顺序。dfs(nums,i+1);path.remove(path.size()-1);}}
}这篇关于二叉搜索树,穷举(全排列)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!