文献研读-Methodology for Performing Synchrophasor Data Conditioning and Validation执行同步相量数据调节和验证的方法

1. 文献来源

Methodology for Performing Synchrophasor Data Conditioning and Validation

2. 摘要

  纯相量测量单元（PMU）状态估计器在速度、性能和可靠性方面本质上优于其SCADA模拟。然而，在将其作为EMS或其他网络应用程序的前端之前，确保进入线性估计器的数据流的质量至关重要。一种方法是在相量数据到达线性估计器之前对其进行预处理。本文提出了一种同步相量数据调节和修复算法，该算法巧妙地作为前缀嵌入到现有的线性状态估计公式中。使用安装在Dominion Virginia Power（DVP）超高压网络中的PMU获得的现场数据对该方法进行了测试。结果表明，该方法为同步相量数据质量问题提供了一种计算简单、优雅的解决方案。

3. 目的

由于相量数据的流性质，使用该数据的下游应用程序容易受到网络拥塞、配置错误、设备故障等的影响。参考文献[3]强调了与PMU数据相关的一些数据质量问题，但没有提供任何算法用于其调节/验证。本文的目的是通过建立一个计算简单有效的模型来调节和修复同步相量数据的质量。

4. 改进思想

复电压和电流遵循式（2），下一个时刻的估计值，取决于之前三个时刻的
$$\hat{\mathrm{x}}(\mathrm{k}+1\mid \mathrm{k})=3\hat{\mathrm{x}}(\mathrm{k}\mid \mathrm{k})-3\hat{\mathrm{x}}(\mathrm{k}-1\mid \mathrm{k}-1)+\hat{\mathrm{x}}(\mathrm{k}-2\mid \mathrm{k}-2)\text{\hspace{1em}(2)}$$

4.1 滤波

式（3）为经典卡尔曼滤波器的状态方程和量测方程：
$$\begin{array}{l}\mathbf{x}(\mathrm{k}+1)=\mathbf{\Phi }(\mathrm{k}+1,\mathrm{k})\mathbf{x}(\mathrm{k})+\mathbf{\Gamma }(\mathrm{k}+1,\mathrm{k})\mathbf{w}(\mathrm{k})\\ \mathbf{z}(\mathrm{k}+1)=\mathbf{H}(\mathrm{k}+1)\mathbf{x}(\mathrm{k}+1)+\mathbf{v}(\mathrm{k}+1)\end{array}\text{\hspace{1em}(3)}$$

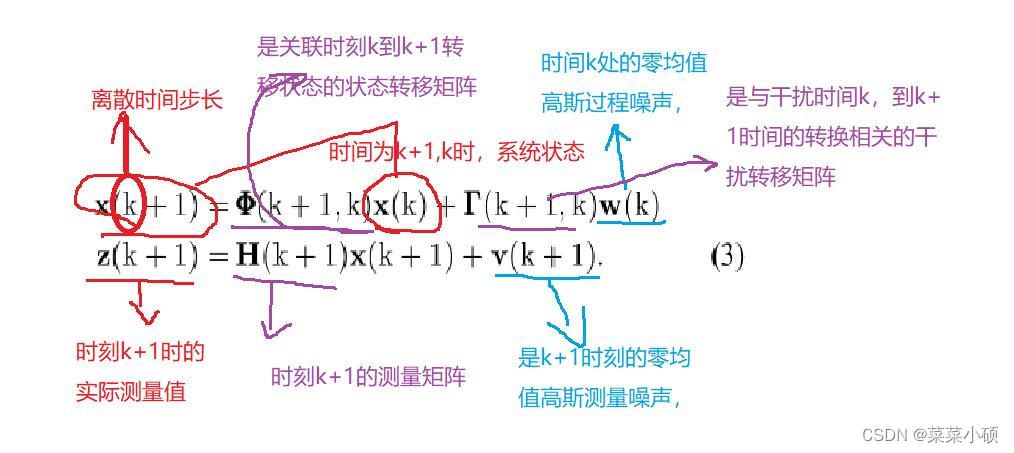
因此，$\mathrm{k}+1$是测量到达并进行估计的当前时间戳。对于最优滤波，我们取（3）的估计值，并将其表示为卡尔曼滤波符号中的递归关系，如（4a）和（4b）所示：
$$\begin{array}{rl}\hat{\mathbf{x}}(\mathrm{k}+1\mid \mathrm{k}+1)& =\mathbf{\Phi }(\mathrm{k}+1,\mathrm{k})\hat{\mathbf{x}}(\mathrm{k}\mid \mathrm{k})\\ & +\mathbf{K}(\mathrm{k}+1)(\mathbf{z}(\mathrm{k}+1)-\hat{\mathbf{z}}(\mathrm{k}+1\mid \mathrm{k}))\end{array}\text{\hspace{1em}(4a)}$$$$\hat{\mathbf{z}}(\mathrm{k}+1\mid \mathrm{k})=\mathbf{H}(\mathrm{k}+1)\hat{\mathbf{x}}(\mathrm{k}+1\mid \mathrm{k})\text{\hspace{1em}(4b)}$$
在（4）中$\mathrm{K}(\mathrm{k}+1)$ 是卡尔曼增益。使用标准卡尔曼滤波技术[11]求解方程（4）。
  当应用于同步相量数据时，可以进一步简化，如下所示。 由于二次预测模型的性质，相邻状态向量共享三个状态变量中的两个，从而产生一个增强状态向量。这可以被视为一个移动窗口，其中包含系统的三个快照，一次只向前移动一个快照。因此，用于基于（2）预测下一个状态，并且$\hat{\mathrm{x}}(\mathrm{k}+1)$和$\hat{\mathrm{x}}(\mathrm{k}+1|\mathrm{k})$可以表示为 :
$$\hat{\mathbf{x}}(\mathrm{k}\mid \mathrm{k})=\left[\begin{array}{c}\hat{\mathrm{x}}(\mathrm{k}\mid \mathrm{k})\\ \hat{\mathrm{x}}(\mathrm{k}-1\mid \mathrm{k}-1)\\ \hat{\mathrm{x}}(\mathrm{k}-2\mid \mathrm{k}-2)\end{array}\right]\text{\hspace{1em}(5a)}$$$$\hat{\mathbf{x}}(\mathrm{k}+1\mid \mathrm{k})=\left[\begin{array}{c}\hat{\mathrm{x}}(\mathrm{k}+1\mid \mathrm{k})\\ \hat{\mathrm{x}}(\mathrm{k}\mid \mathrm{k})\\ \hat{\mathrm{x}}(\mathrm{k}-1\mid \mathrm{k}-1)\end{array}\right]\text{\hspace{1em}(5b)}$$
由于未来状态的估计取决于之前的三个状态估计，出于过滤目的，将$\hat{\mathrm{x}}(\mathrm{k}|\mathrm{k})$和$\hat{\mathrm{x}}(\mathrm{k}+1|\mathrm{k})$和描述为3x1矩阵是有意义的。现在，我们知道了$\Phi (\mathrm{k}+1,\mathrm{k})$将$\mathrm{k}+1$和$\mathrm{k}$等时刻状态关联。
$$\hat{\mathbf{x}}(\mathrm{k}+1\mid \mathrm{k})=\mathbf{\Phi }(\mathrm{k}+1,\mathrm{k})\hat{\mathbf{x}}(\mathrm{k}\mid \mathrm{k})\text{\hspace{1em}(5c)}$$
因此，基于（2）、（5a）、（5b）和（5c），$\Phi (\mathrm{k}+1,\mathrm{k})$可以公式化为常数，如（5d）所示：
$$\mathbf{\Phi }(\mathrm{k}+1,\mathrm{k})=\left[\begin{array}{ccc}3& -3& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]\text{\hspace{1em}(5d)}$$
这里需要注意的是，（5a）和（5b）中的状态是复电压和电流测量值。因此，在不失一般性的情况下，我们可以写出（5e）和（5f）：
$$\mathrm{z}(\mathrm{k}+1)=\mathrm{x}(\mathrm{k}+1)+\mathrm{v}(\mathrm{k}+1)\text{\hspace{1em}(5e)}$$$$\hat{\mathrm{z}}(\mathrm{k}+1|k)=\hat{\mathrm{z}}(\mathrm{x}+1|k)\text{\hspace{1em}(5f)}$$
使用（4b）中的（5b）和（5f），我们得到$\mathrm{H}(\mathrm{k}+1)$
$$\mathrm{H}(\mathrm{k}+1)=[101]\text{\hspace{1em}(5g)}$$
因此，在分别替换（4a）和（4b）的RHS中的（5d）和（5g）时，将开发滤波技术的简化模型，如（6a）和（6b）所示
$$\begin{array}{rl}\hat{\mathbf{x}}(\mathrm{k}+1\mid \mathrm{k}+1)& =\left[\begin{array}{ccc}3& -3& 1\\ 1& 0& 0\\ 0& 1& 0\end{array}\right]\hat{\mathbf{x}}(\mathrm{k}\mid \mathrm{k})\\ & +\mathbf{K}(\mathrm{k}+1)(\mathrm{z}(\mathrm{k}+1)-\hat{\mathrm{z}}(\mathrm{k}+1\mid \mathrm{k}))\end{array}\text{\hspace{1em}(6a)}$$
$$\hat{\mathbf{z}}(\mathrm{k}+1\mid \mathrm{k})=\left[\begin{array}{lll}1& 0& 0\end{array}\right]\hat{\mathbf{x}}(\mathrm{k}+1\mid \mathrm{k})\text{\hspace{1em}(6b)}$$
（6a）的RHS中的第二项对应于稳态观测残差。卡尔曼增益由以下方程组指定：
$$\begin{array}{rl}\mathbf{K}(\mathrm{k}+1)=& \mathbf{P}(\mathrm{k}+1\mid \mathrm{k}){\mathbf{H}}^{\mathrm{T}}(\mathrm{k}+1)\\ & \times [\mathbf{H}(\mathrm{k}+1)\mathbf{P}(\mathrm{k}+1\mid \mathrm{k}){\mathbf{H}}^{\mathrm{T}}(\mathrm{k}+1)\\ & +\mathbf{R}(\mathrm{k}+1){]}^{-1}\end{array}\text{\hspace{1em}(7a)}$$
$$\begin{array}{rl}\mathbf{P}(\mathrm{k}+1\mid \mathrm{k})=& \mathbf{\Phi }(\mathrm{k}+1,\mathrm{k})\mathbf{P}(\mathrm{k}\mid \mathrm{k}){\mathbf{\Phi }}^{\mathrm{T}}(\mathrm{k}+1,\mathrm{k})\\ & +\Gamma (\mathrm{k}+1,\mathrm{k})\mathbf{Q}(\mathrm{k}){\mathbf{\Gamma }}^{\mathrm{T}}(\mathrm{k}+1,\mathrm{k})\end{array}\text{\hspace{1em}(7b)}$$
$$\mathbf{P}(\mathrm{k}+1\mid \mathrm{k}+1)=[\mathbf{I}-\mathbf{K}(\mathrm{k}+1)\mathbf{H}(\mathrm{k}+1)]\mathbf{P}(\mathrm{k}+1\mid \mathrm{k})\text{\hspace{1em}(7c)}$$
因为各个状态是不相关的$\mathrm{R}(\mathrm{k}+1)=\mathrm{R}$，且$\mathrm{Q}(\mathrm{k})=\mathrm{Q}$等，他们都是标量。现场数据的这两个量的典型值为$10^{-2}$。 此外，$3\times 1$初始状态向量和$3\times 3$初始估计误差协方差$\mathrm{P}(0|0)$是零矩阵。 原因是，只要确认在第一个窗口完全填充数据之前，初始状态向量和初始估计误差协方差的值将不正确，则初始状态向量和初始估计误差协方差的值将不会影响模拟。
这样做的目的：就是把传感器测得的值和根据数学模型推导出来的值融合以逼近实际值的过程。

4.2 平滑

平滑算法使用电流测量值估计系统的先前状态。从数学上讲，这意味着求解$\hat{\mathrm{x}}(k|j)$当$j>k$时。 与滤波相比，平滑的优势在于，通过平滑，可以显著提高估计的质量[13]。与用于滤波目的的同步相量数据相关的二次预测模型也适用于平滑过程。本文中使用的固定滞后平滑器模型在[14]中开发。它有一个离散时间状态方程，其形式为递归卡尔曼滤波器，带有一个增强状态向量、一个相关的增强动力系统和一个增强测量方程，如（8）所示（有关它的更多详细信息，请参见[11]和[14]）：
$$\begin{array}{l}\left[\begin{array}{c}\hat{\mathbf{x}}(\mathrm{k}+1\mid \mathrm{k}+1)\\ \hat{\mathbf{x}}(\mathrm{k}\mid \mathrm{k}+1)\\ \hat{\mathbf{x}}(\mathrm{k}-1\mid \mathrm{k}+1)\\ ⋮\\ \hat{\mathbf{x}}(\mathrm{k}+1-\mathrm{N}\mid \mathrm{k}+1)\end{array}\right]\\ =\left[\begin{array}{ccccc}\mathbf{\Phi }(\mathrm{k}+1,\mathrm{k})& 0& 0& \dots & 0\\ \mathbf{I}& 0& 0& \dots & 0\\ 0& \mathbf{I}& 0& \dots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& \dots & \mathbf{I}& 0\end{array}\right]\left[\begin{array}{c}\hat{\mathbf{x}}(\mathrm{k}\mid \mathrm{k})\\ \hat{\mathbf{x}}(\mathrm{k}-1\mid \mathrm{k})\\ \hat{\mathbf{x}}(\mathrm{k}-2\mid \mathrm{k})\\ ⋮\\ \mathbf{K}\mid \mathrm{k})\end{array}\right]\\ +\left[\begin{array}{c}\mathbf{K}(\mathrm{k}+1)\\ {\mathbf{K}}_1(\mathrm{k}+1)\\ {\mathbf{K}}_2(\mathrm{k}+1)\\ ⋮\\ {\mathbf{K}}_{\mathrm{N}}(\mathrm{k}+1)\end{array}\right](\mathrm{z}(\mathrm{k}+1)-\mathbf{H}(\mathrm{k}+1)\hat{\mathbf{x}}(\mathrm{k}+1\mid \mathrm{k}))\end{array}\text{\hspace{1em}(8)}$$
在（8）中，N是窗口长度，其中$\mathrm{K}(\mathrm{k}+1),{\mathrm{K}}_1(\mathrm{k}+1),...,{\mathrm{K}}_{\mathrm{N}}(\mathrm{k}+1)$是增益矩阵。方程（8）可以递归求解，如[14]所示。 （8）中的矩阵$\Phi (\mathrm{k}+1,\mathrm{k})$和$\mathrm{H}(\mathrm{k}+1)$具有与上一小节中计算的相同的维数和值。 明智地选择窗口长度很重要，因为虽然N的值越高，接收测量和平滑状态估计之间的延迟越大，但它也会显著提高估计的质量。 其原因是，使用$\hat{\mathrm{x}}(\mathrm{k}+1-N|k+1)$获得的估计直观上优于使用$\hat{\mathrm{x}}(\mathrm{k}+1-N|k+1-\mathrm{N})$获得的估计。对于本文所做的模拟$N=3$。在下一节中，将说明这种基于二次预测模型的卡尔曼滤波器用于调节从现场获得的实际同步相量数据的性能。

5. 模型预测控制-MPC

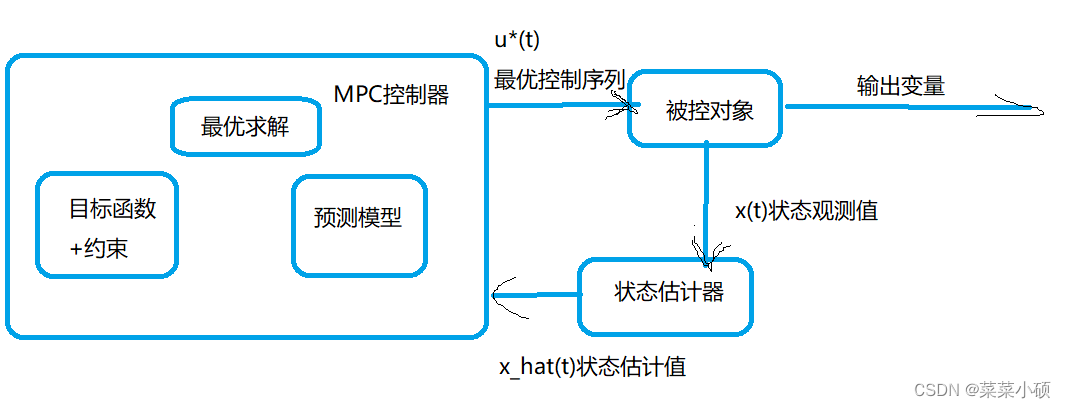模型预测控制：
模型预测控制在实现过程中有3个关键步骤：预测模型、滚动优化和反馈校正。

1. 预测模型：预测模型是模型预测控制的基础。其主要功能是根据对象的历史信息和未来输入,预测系统未来的输出。对预测模型的形式没有做严格的限定,状态方程、传递函数这类传统的模型都可以作为预测模型。对于线性稳定系统,阶跃响应、脉冲响应这类非参数模型,也可以直接作为预测模型使用。
2. 滚动优化：预测控制中的优化与通常的离散最优控制算法不同，不是采用一个不变的全局最优目标，而是采用滚动式的有限时域优化策略。在每一采样时刻，根据该时刻的优化性能指标，求解该时刻起有限时段的最优控制率。计算得到的控制作用序列也只有当前值是实际执行的，在下一个采样时刻又重新求取最优控制率。也就是说，优化过程不是一次离线完成的，而是反复在线进行的，即在每一采样时刻，优化性能指标只涉及从该时刻起到未来有限的时间，而到下一个采样时刻，这一优化时段会同时向前推移。
3. 反馈校正：为了防止模型失配或者环境干扰引起控制对理想状态的偏离,在新的采样时刻,首先检测对象的实际输出,并利用这一实时信息对基于模型的预测结果进行修正,然后再进行新的优化。

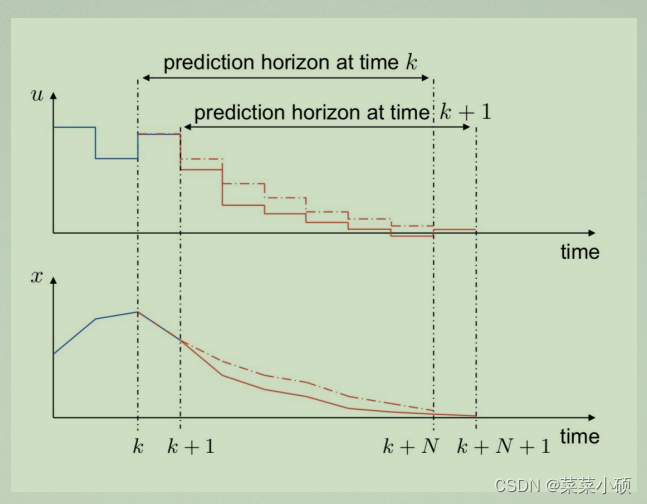
模型预测，预测采样时刻$k$之后的$i$时刻的数值。

6. 总结

  该文基于经典卡尔曼滤波器滤波及平滑，对纯相量测量单元（PMU）采集到的同步向量数据进行进行数据调节，以此来获得质量较高的同步相量估计值。该数据估计算法和应用至MPC中，用于提高状态估计器估计值的质量。
  关于卡尔曼滤波的基础知识可以参考郑政谋老师主编的《最佳线性滤波——维纳滤波、卡尔曼滤波与最小二乘滤波》，该书详细推导了卡尔曼滤波的递推式，卡尔曼增益的求解公式等。需要知道的一点，卡尔曼滤波是一种最优理论，卡尔曼滤波可以使估计出来的噪声值较低，通过加权估计值与测量值，使得最优估计值接近真实值，这样就降低了估计出来的噪声，也就是所谓的“滤波”。
  该文为数据处理提交数据质量提供了思路。