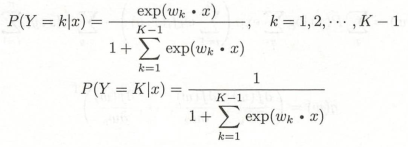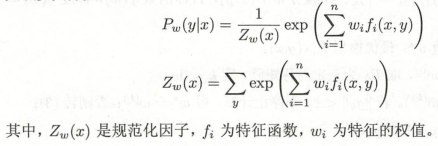[统计学习方法习题实战]Task06:Logistic回归与最大熵模型

logistic回归模型

logistic分布

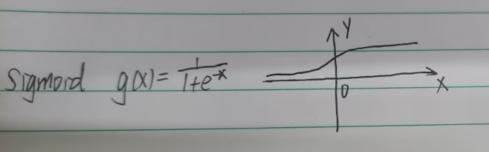
代入求相等
分布函数求导是密度函数

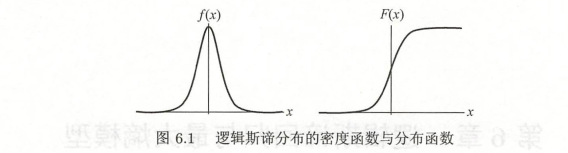
6.1.2 二项logistic回归模型

模型、策略和算法

6.1.3 模型参数估计

有时候等于0是无法求出来的，这个时候就需要用到迭代的方法无限逼近那个点，梯度下降法

6.1.4 多项logistic回归

这里wk是向量

6.2 最大熵模型

6.2.1 最大熵原理

最大熵原理看书上的有点看不懂，咋说呢，没有和我的灵魂产生共鸣，所以我找了容易看懂的资料：图解最大嫡原理(The Maximum Entropy Principl)

信息嫡的定义的确能够描述并且量化那些生活中看起来很简单但是却总觉得有点说不清楚的问题。

最大嫡原理的本质:系统中事件发生的概率满足一切已知约束条件，不对任何未知信息做假设，也就是对于未知的，当作等概率处理。

6.2.2 最大熵模型的定义

6.2.3 最大熵模型的学习

求偏导部分要着重注意

这个例题不错，我个人比较喜欢看例题，在题目里学习，因为有时候概念文字看的太迷糊了，题目就很清楚。
这里这个例题还是不错的对于我个人来说
这里给人感觉比较难的是求偏导部分，但其实只是看着繁琐，难度不高

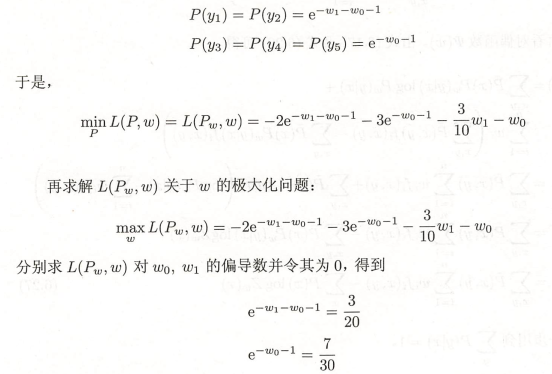
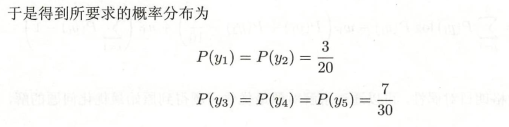
6.2.4 极大似然估计

对偶函数的极大化等价于最大熵模型的极大似然估计

这里要用到联合概率分布的知识，最优解P(y|x)的部分为1，所以有些式子会莫名其妙消失

模型学习就是在给定的训练数据条件下对模型进行极大似然估计或正则化的极大似然估计。

6.3 模型学习的最优化算法

6.3.1 改进的迭代尺度法

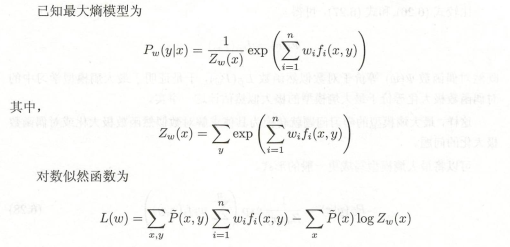
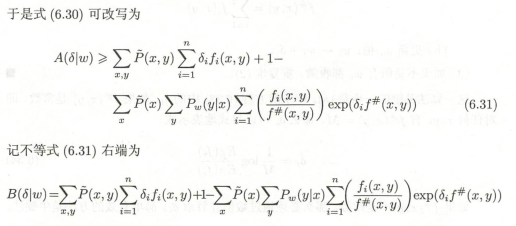
Jensen不等式如下：

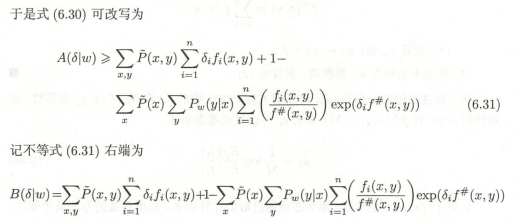
6.3.2 拟牛顿法

作业

1

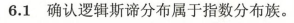
指数族分布简介
百度的不知道为什么，总感觉有问题，这个定义写的更加清晰

2

这个是附录A的梯度下降法说明

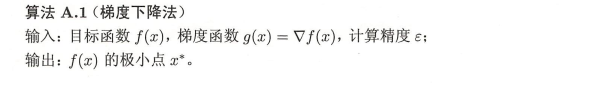
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap #指定颜色，列出的颜色映射
import pandas as pdcmap_light = ListedColormap(['#FFAAAAA','#AAFFAA','#AAAFF'])
cmap_bold = ListedColormap(['#FF0000','#00FF00','#0000FF'])#数据读入
y = np.array([1.0,1.0,-1.0,-1.0,-1.0])
x = np.array([[-1.0,1.0],[-1.0,-1.0],[1.0,1.0],[1.0,-1.0],[0.0,1.0]])#加上截距项
b = np.ones([len(x),1])
x = np.concatenate([x, b], 1)#随机初始化
omega = np.array([0.0,0.0,0.0])
eta = 0.2#模型函数
def prob(xi,omega):exp = np.exp(np.dot(xi,omega))return exp / (1.0 + exp)#似然函数
y_pred = np.array([np.sign(prob(xi,omega) - 0.5) for xi in x]) #这里用了解析表达式lost_df = pd.DataFrame()lost = -1.0 / len(x) * np.sum(np.array([yi * (np.dot(xi,omega)) -np.log(1.0 + np.exp(np.dot(xi, omega))) for xi,yi in zip(x, y)]))g = (prob(x[0],omega) - y[0]) * x[0]
omega = omega - eta * glost_n = -1.0 / len(x) * np.sum(np.array([yi * (np.dot(omega, xi)) -np.log(1.0 + np.exp(np.dot(omega, xi))) for xi,yi in zip(x, y)]))for ii in range(1000):for xi,yi in zip(x, y):lost_series = pd.Series()lost_series['lost'], lost_series['lost_change'] = lost_n, lost_n - lostlost_series.name = iilost_df = lost_df.append(lost_series)lost = lost_ng = (prob(xi, omega) - yi) * xiomega = omega - eta * glost_n = -1.0 / len(x) * np.sum(np.array([yi * (np.dot(omega, xi)) -np.log(1+np.exp(np.dot(omega,xi))) for xi,yi in zip(x,y)]))#结果展示
xx = np.linspace(np.min(x[0,:]) - 1.0, np.max(x[0,:]) + 1, 200)
yy = np.linspace(np.min(x[1,:]) - 1.0, np.max(x[1,:]) + 1, 200)xx,yy = np.meshgrid(xx, yy)
Z = np.array([np.sign(prob(xi, omega) - 0.5) for xi inzip(xx.ravel(), yy.ravel(), np.ones(xx.shape).ravel())]).reshape(xx.shape)plt.figure()
plt.pcolormesh(xx, yy, Z, cmap=cmap_light) #绘制预测结果图
plt.scatter(x[:,0], x[:,1], c=y, cmap=cmap_bold)
plt.grid()plt.figure()
lost_df['lost_change'].plot()plt.figure()
lost_df['lost'].plot()

迭代那里总是报错，像鼠

3

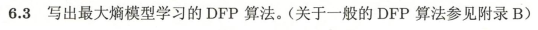
附录B说明如下：

黑塞矩阵是在梯度的基础上求偏导，如下图：

这算法是三个人名字凑一起的，没啥字面意思

有点像凑配法是怎么回事（肯定是我没有理解算法真谛）


这第四个方法有种很牛但是我有点get不到牛在哪的感觉，应该是在红框部分，在前面的算法上进行了改良——这里是逼近思想？我个人猜想是黑塞矩阵实际上不好算，所以用另外一个式子进行了逼近？就是相当于还是想要黑塞矩阵又想优化运行


接下来回到作业里的DFP算法：

python代码实现找到个大佬的手写李航《统计学习方法》书中全部算法(已完成71)

人和人的差距比人和*的大

具体的DFP算法实现如下拟牛顿法实现的最大嫡模型(原生Python实现)

大佬用的是最火的BFGS算法

代码写的很漂亮，注释很全，阅读无难度

import math
import numpy as np
from scipy.misc import derivativedef golden_section_for_line_search(func, a0, b0, epsilon):"""一维搜索极小值点（黄金分割法）:param func: [function] 一元函数:param a0: [int/float] 目标区域左侧边界:param b0: [int/float] 目标区域右侧边界:param epsilon: [int/float] 精度"""a1, b1 = a0 + 0.382 * (b0 - a0), b0 - 0.382 * (b0 - a0)fa, fb = func(a1), func(b1)while b1 - a1 > epsilon:if fa <= fb:b0, b1, fb = b1, a1, faa1 = a0 + 0.382 * (b0 - a0)fa = func(a1)else:a0, a1, fa = a1, b1, fbb1 = b0 - 0.382 * (b0 - a0)fb = func(b1)return (a1 + b1) / 2def partial_derivative(func, arr, dx=1e-6):"""计算n元函数在某点各个自变量的梯度向量（偏导数列表）:param func: [function] n元函数:param arr: [list/tuple] 目标点的自变量坐标:param dx: [int/float] 计算时x的增量:return: [list] 偏导数"""n_features = len(arr)ans = []for i in range(n_features):def f(x):arr2 = list(arr)arr2[i] = xreturn func(arr2)ans.append(derivative(f, arr[i], dx=dx))return ansdef bfgs_algorithm_for_maximum_entropy_model(x, y, features, error=1e-6, distance=20, maximum=1000):"""最大熵模型学习的BFGS算法:param x: 输入变量:param y: 输出变量:param features: 特征函数列表:param error: [int/float] 学习精度:param distance: [int/float] 每次一维搜索的长度范围（distance倍梯度的模）:param maximum: [int] 最大学习次数:return: [list] 结果点坐标"""n_samples = len(x)  # 样本数量n_features = len(features)  # 特征函数数量# 坐标压缩（将可能存在的非数值的特征及类别转换为数值）y_list = list(set(y))y_mapping = {c: i for i, c in enumerate(y_list)}x_list = list(set(tuple(x[i]) for i in range(n_samples)))x_mapping = {c: i for i, c in enumerate(x_list)}n_x = len(x_list)  # 不同的x的数量n_y = len(y_list)  # 不同的y的数量print(x_list, x_mapping)print(y_list, y_mapping)# 计算联合分布的经验分布:P(X,Y) (empirical_joint_distribution)d1 = [[0.0] * n_y for _ in range(n_x)]  # empirical_joint_distributionfor i in range(n_samples):d1[x_mapping[tuple(x[i])]][y_mapping[y[i]]] += 1 / n_samplesprint("联合分布的经验分布:", d1)# 计算边缘分布的经验分布:P(X) (empirical_marginal_distribution)d2 = [0.0] * n_x  # empirical_marginal_distributionfor i in range(n_samples):d2[x_mapping[tuple(x[i])]] += 1 / n_samplesprint("边缘分布的经验分布", d2)# 计算特征函数关于经验分布的期望值:EP(fi) (empirical_joint_distribution_each_feature)# 所有特征在(x,y)出现的次数:f#(x,y) (samples_n_features)d3 = [0.0] * n_features  # empirical_joint_distribution_each_featurenn = [[0.0] * n_y for _ in range(n_x)]  # samples_n_featuresfor j in range(n_features):for xi in range(n_x):for yi in range(n_y):if features[j](list(x_list[xi]), y_list[yi]):d3[j] += d1[xi][yi]nn[xi][yi] += 1print("特征函数关于经验分布的期望值:", d3)print("所有特征在(x,y)出现的次数:", nn)def func(ww):"""目标函数"""res = 0for xxi in range(n_x):t1 = 0for yyi in range(n_y):t2 = 0for jj in range(n_features):if features[jj](list(x_list[xxi]), y_list[yyi]):t2 += ww[jj]t1 += pow(math.e, t2)res += d2[xxi] * math.log(t1, math.e)for xxi in range(n_x):for yyi in range(n_y):t3 = 0for jj in range(n_features):if features[jj](list(x_list[xxi]), y_list[yyi]):t3 += ww[jj]res -= d1[xxi][yyi] * t3return res# 定义w的初值和B0的初值w0 = [0] * n_features  # w的初值：wi=0B0 = np.identity(n_features)  # 构造初始矩阵G0(单位矩阵)for k in range(maximum):# 计算梯度 gknabla = partial_derivative(func, w0)g0 = np.matrix([nabla]).T  # g0 = g_k# 当梯度的模长小于精度要求时，停止迭代if pow(sum([nabla[i] ** 2 for i in range(n_features)]), 0.5) < error:break# 计算pkif k == 0:pk = - B0 * g0  # 若numpy计算逆矩阵时有0，则对应位置会变为infelse:pk = - (B0 ** -1) * g0# 一维搜索求lambda_kdef f(xx):"""pk 方向的一维函数"""x2 = [w0[jj] + xx * float(pk[jj][0]) for jj in range(n_features)]return func(x2)lk = golden_section_for_line_search(f, 0, distance, epsilon=1e-6)  # lk = lambda_k# print(k, "lk:", lk)# 更新当前点坐标w1 = [w0[j] + lk * float(pk[j][0]) for j in range(n_features)]# print(k, "w1:", w1)# 计算g_{k+1}，若模长小于精度要求时，则停止迭代# 计算新的模型nabla = partial_derivative(func, w1)g1 = np.matrix([nabla]).T  # g0 = g_{k+1}# 当梯度的模长小于精度要求时，停止迭代if pow(sum([nabla[i] ** 2 for i in range(n_features)]), 0.5) < error:w0 = w1break# 计算G_{k+1}yk = g1 - g0dk = np.matrix([[lk * float(pk[j][0]) for j in range(n_features)]]).TB1 = B0 + (yk * yk.T) / (yk.T * dk) + (B0 * dk * dk.T * B0) / (dk.T * B0 * dk)B0 = B1w0 = w1p1 = [[0.0] * n_y for _ in range(n_x)]for xi in range(n_x):for yi in range(n_y):for j in range(n_features):if features[j](list(x_list[xi]), y_list[yi]):p1[xi][yi] += w0[j]p1[xi][yi] = pow(math.e, p1[xi][yi])total = sum(p1[xi][yi] for yi in range(n_y))if total > 0:for yi in range(n_y):p1[xi][yi] /= totalans = {}for xi in range(n_x):for yi in range(n_y):ans[(tuple(x_list[xi]), y_list[yi])] = p1[xi][yi]return w0, ansif __name__ == "__main__":dataset = [[[1], [1], [1], [1], [2], [2], [2], [2]], [1, 2, 2, 3, 1, 1, 1, 1]]def f1(xx, yy):return xx == [1] and yy == 1def f2(xx, yy):return (xx == [1] and yy == 2) or (xx == [1] and yy == 3)# {((1,), 1): 0.2500000558794252, ((1,), 2): 0.3749999720602874, ((1,), 3): 0.3749999720602874, ((2,), 1): 0.3333333333333333, ((2,), 2): 0.3333333333333333, ((2,), 3): 0.3333333333333333}print(bfgs_algorithm_for_maximum_entropy_model(dataset[0], dataset[1], [f1]))# {((1,), 1): 0.24999946967330844, ((1,), 2): 0.3750002651633458, ((1,), 3): 0.3750002651633458, ((2,), 1): 0.3333333333333333, ((2,), 2): 0.3333333333333333, ((2,), 3): 0.3333333333333333}print(bfgs_algorithm_for_maximum_entropy_model(dataset[0], dataset[1], [f2]))

总结

1.logistic回归模型是由以下条件概率分布表示的分类模型。logistic回归模型可以用于二类或多类分类。

2.最大嫡模型是由以下条件概率分布表示的分类模型。最大嫡模型也可以用于二类或多类分类。

3.最大嫡模型可以由最大嫡原理推导得出。
最大嫡原理应用到分类模型的学习中，有以下约束最优化问题:

4.logistic回归模型与最大嫡模型都属于对数线性模型。
5.logistic回归模型及最大嫡模型学习一般采用极大似然估计，或正则化的极大似然估计。