维纳滤波最陡下降法 matlab仿真

本文主要是介绍维纳滤波最陡下降法 matlab仿真，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

% 最陡下降算法仿真实例 现代数字信号处理及其应用 4.3.4
close all 
clc
% 模拟产生输入随机序列u(n)
% 迭代步长 0.02
q = 0.02;
N = 1000;% 2抽头维纳滤波器，迭代次数为N
W = zeros(2, N);
R = [1.0997 0.4997; 0.4997 1.0997]
% 其中D为特征值构成的对角阵，特征向量为V
[V, D] = eig(R)%通过上式求出最大特征值是1.5994，u < 2/1.5994 = 1.2505
%所以u如果大于1.25，迭代次数越多，并不会使Jmin收敛。
%反之，u小于1.25，相对来说迭代越多，Jmin越收敛，并且u越小，收敛越慢。p = [0.5270 -0.4458]'
%期望信号d(n)的平均功率或方差
var_d = 0.9486%w(n+1) = w(n) + u[p - Rw(n)]
%J(w(n)) = σd^2 - p'w(n)
for n = 1 : N - 1W(:, n+1) = W(:, n) + q * (p - R * W(:, n));J(n) = var_d - p'* W(:, n);
end
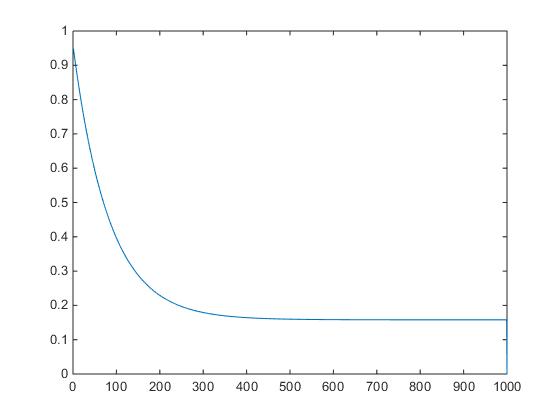
Jmin = J(n)figure
n=1 : N;  
plot(n,W(1, :),n,W(2, :))figure
n=1 : N;  
plot(n, J(n))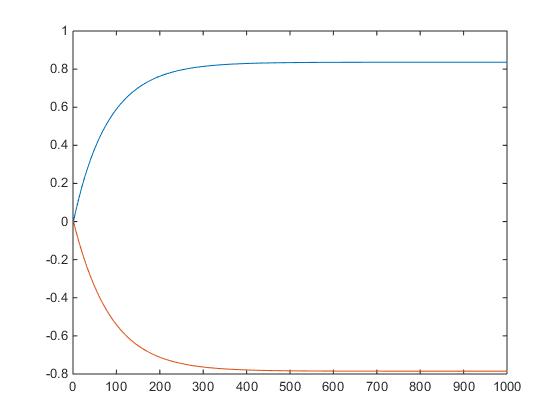

这篇关于维纳滤波最陡下降法 matlab仿真的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---