了解面试必会算法Sliding Window 模式的前世今生

本文主要是介绍了解面试必会算法Sliding Window 模式的前世今生，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

大家好，今天我们来聊一聊sliding window pattern。又是给有个机会给班花讲题的好机会，不能错过！
在这里插入图片描述

Sliding Window Pattern，中文名字叫滑动窗口模式，是一种常见的算法思想。它可以用来解决很多问题，比如：

Sliding Window Pattern 的优缺点

它具有以下优点：

可以有效地解决很多问题：Sliding Window Pattern 可以用于解决很多问题，比如求最大值、最小值、平均值、子串、子序列的长度、最长公共子序列、最长上升子序列等。
时间复杂度较低：Sliding Window Pattern 的一般时间复杂度为 O(n)，对于一些特殊问题，时间复杂度甚至可以达到 O(1)。
代码实现简单：Sliding Window Pattern 的代码实现非常简单，只需要维护一个窗口，然后在窗口滑动过程中不断地更新窗口内的值即可。

Sliding Window 算法也存在一些缺点：

需要额外空间：Sliding Window Pattern 需要额外存储窗口内的元素，因此会增加空间复杂度。
适用范围有限：Sliding Window Pattern 并不是所有问题都适用，只有满足特定条件的问题才能使用 Sliding Window Pattern。

怎么样？是不是依然觉得有些不理解，那么上图说话
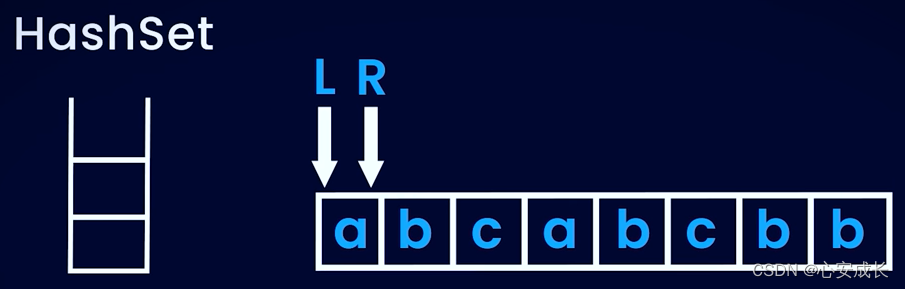
在这里插入图片描述
L和R指针分别都指向a, R走到b，这时候将a放入HashSet，接下来放入b；因为窗口大小为3，那么R继续向➡️走，走到c，最终将c放入HashSet。

当然了如何白月光还是觉得这个算法不好记，我们就那个例子让她印象更加深刻吧

我们可以把数组看成一条河流，窗口就像一条船。船从左到右航行，每次经过一个元素，就把这个元素记录下来。当船航行到河流的尽头时，我们就得到了河流中最大值的滑动窗口。

伪代码实现

function sliding_window(array, window_size)# 初始化窗口window = []for i in range(window_size):window.append(array[i])# 滑动窗口for i in range(window_size, len(array)):# 更新窗口window.pop(0)window.append(array[i])# 计算窗口内的值...# 返回窗口内的值return window