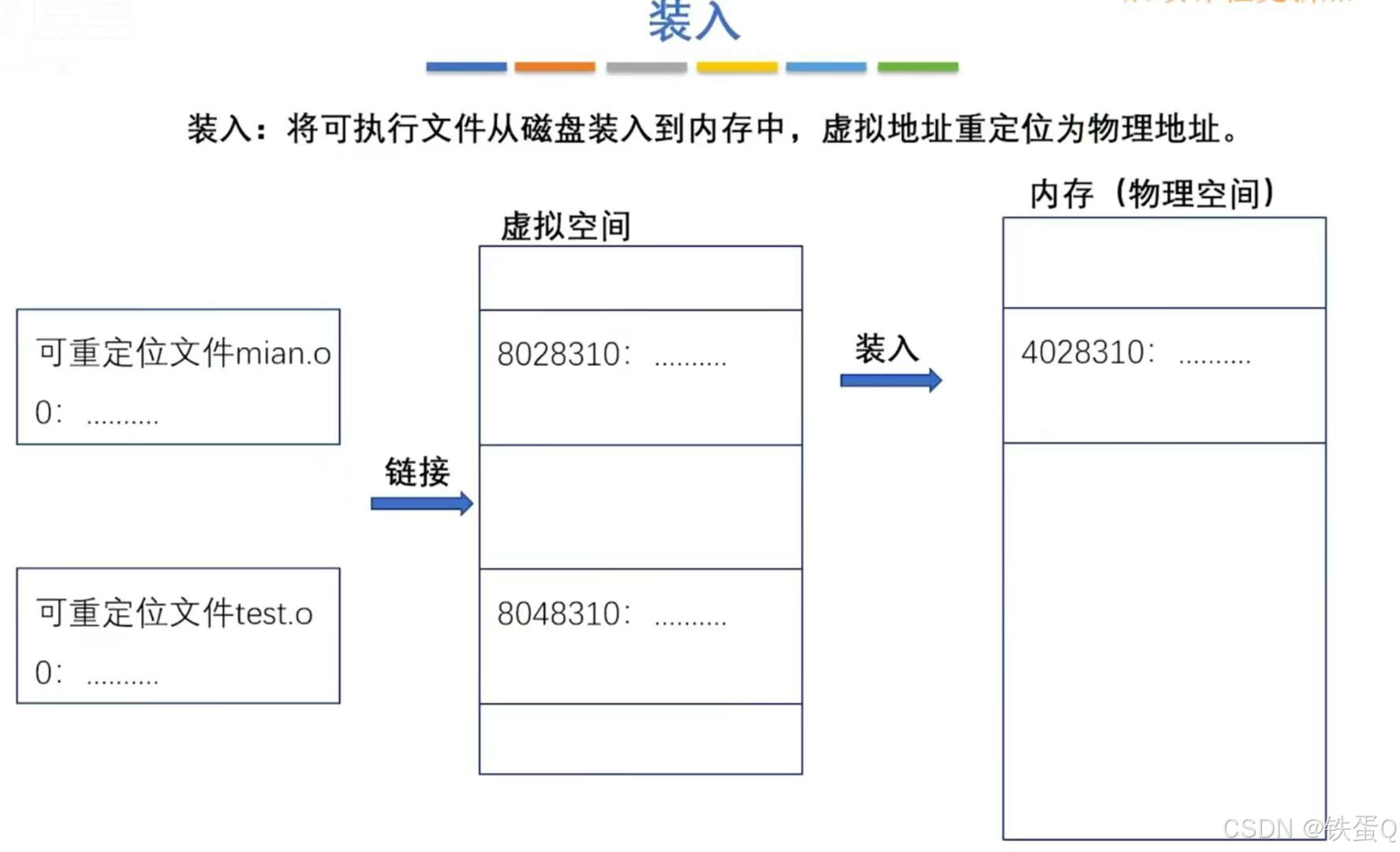
本文主要是介绍三元组和十字链,稀疏矩阵(画图教你稀疏矩阵的三元组和十字链表示),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
数据结构专升本学习,稀疏矩阵(三元组和十字链)
前言:
前面我们简单学了,数组和几种简单的压缩存储,今天我们学习一下稀疏矩阵,稀疏矩阵的存储方法只存储非零元素,主要有三元组和十字链两种方法,接下来我会尽量让大家明白这个东西,没学会也没关系,博主自我感觉这个东西不怎么重要,当然只是对我自己而言,因为我现在都没遇到过项目说优化要使用稀疏矩阵来优化。哈哈哈,可能博主做过的项目少吧,好了,不多聊了我们进入主题。
每日一遍,防止颓废

(双十一了,别人在剁手,我们穷的在吃土🤣🤣🤣)
1.什么是稀疏矩阵
在矩阵中,若数值为0的元素数目远远多于非0元素的数目,并且非0元素分布没有规律时,则称该矩阵为稀疏矩阵;与之相反,若非0元素数目占大多数时,则称该矩阵为稠密矩阵。定义非零元素的总数比上矩阵所有元素的总数为矩阵的稠密度。官方定义是:矩阵中非零元素的个数远远小于矩阵元素的总数,并且非零元素的分布没有规律,通常认为矩阵中非零元素的总数比上矩阵所有元素总数的值小于等于0.05时,则称该矩阵为稀疏矩阵(sparse matrix),该比值称为这个矩阵的稠密度;与之相区别的是,如果非零元素的分布存在规律(如上三角矩阵、下三角矩阵、对角矩阵),则称该矩阵为特殊矩阵。比较基本的定义是矩阵中的大多数元素为零,并且可以利用零元素节约大量存储、运算和程序运行时间。讲人话就是:(有一个矩阵,然后里面的元素是没有规律的,其他的都是零,非零占5%,零占95%的矩阵)
2.稀疏矩阵的三元组表示
三元组是指形如((x,y),z)的集合(这就是说,三元组是这样的偶,其第一个射影亦是一个偶),常简记为(x,y,z)。三元组是计算机专业的一门公共基础课程——数据结构里的概念。主要是用来存储稀疏矩阵的一种压缩方式,也叫三元组表。假设以顺序存储结构来表示三元组表(triple table),则得到稀疏矩阵的一种压缩存储方式,即三元组顺序表,简称三元组表。讲人话就是:(三元组就是有三个元素,前面两看成二维数组的行列号,最后一个数表示这个二维数组里面存的值,阿巴阿巴)😜😜😜
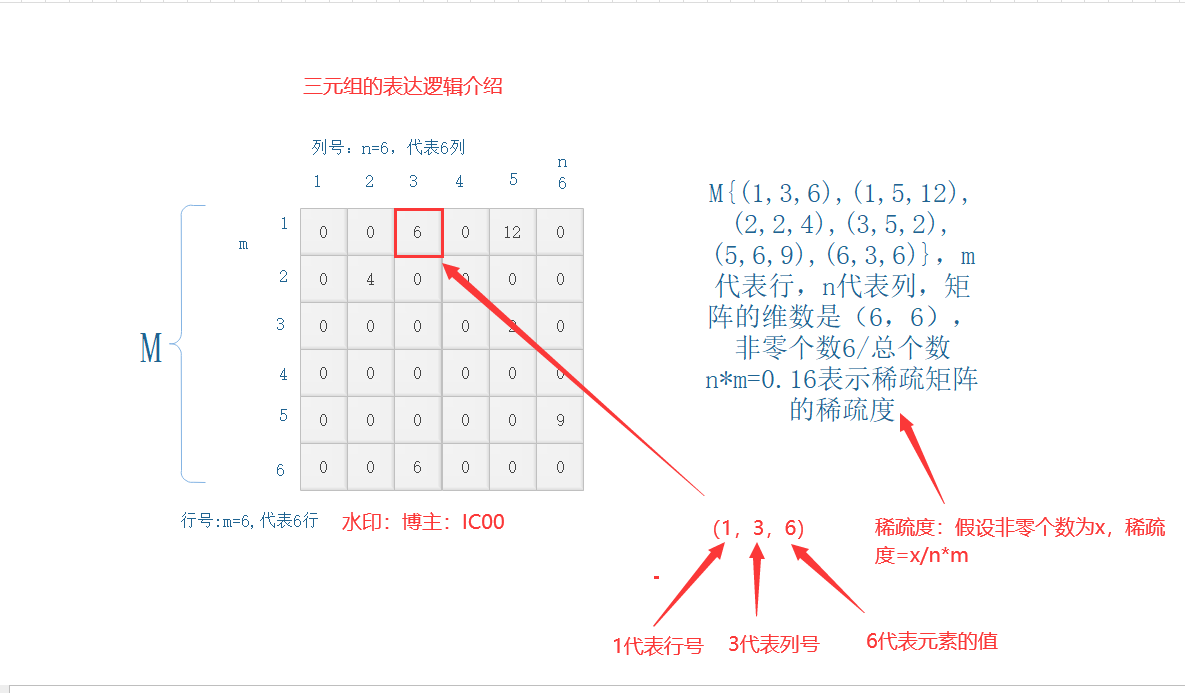
注:博主为了方便起始是行号列好起始是1,有些起始是零
#include <stdio.h>
#include<stdio.h>
#include<stdlib.h>
#define m 6
#define n 6
#define MAXSIZE 100//假设非零元个数的最大值为100
//稀疏矩阵的三元组顺序表存储表示
typedef struct{int i,j;//行下标和列下标int e; //元素值
}node;
typedef struct{node data[MAXSIZE+1];//非零元三元组表,data[0]未用 博主下记录下标从1开始 int mu,nu,tu;//行数、列数、非零元个数 ,记录好行列,非零个数方便还原数组
}TSMatrix;
int CreTSMatrix(TSMatrix *M,int a[m][n])//创建赋值三元矩阵
{int i,j,k=1;//循环遍历i代表行,j代表列,k代表三元组下标,从1开始 (*M).mu=m;//赋值行总数 (*M).nu=n;//赋值列总数 for(i=0;i<m;i++){for(j=0;j<n;j++){if(a[i][j]!=0)//记录非零值 {(*M).data[k].i = (i+1);//记录行号 (*M).data[k].j = (j+1);//记录列号 (*M).data[k].e = a[i][j];//记录元素值 k++;//下标加一 }}} (*M).tu=k-1;//得到非零总个数减一是因为初值为1 return 1;
}
int PrintTSM(TSMatrix M)//输出三元矩阵
{if(M.mu==0||M.nu==0)//判断行列是不是为0 {printf("矩阵为空!\n");return 1;}printf("行数为%d,列数为%d\n",M.mu,M.nu);if(M.tu==0)//判断非零个数为零 {printf("矩阵为零矩阵!\n");return 1;}int k;for(k=1;k<=M.tu;k++)//循环遍历输出 printf("%d\t%d\t%d\n",M.data[k].i,M.data[k].j,M.data[k].e);return 1;
}
//主函数测试
int main() {TSMatrix M;int i,j;int a[m][n]={{0,0,6,0,12,0},{0,4,0,0,0,0},{0,0,0,0,2,0},{0,0,0,0,0,0},{0,0,0,0,0,9},{0,0,6,0,0,0}};printf("打印输出原矩阵:\n");for(i=0;i<m;i++){for(j=0;j<n;j++)printf("%3d",a[i][j]);printf("\n");} CreTSMatrix(&M,a);printf("三元矩阵为:\n");PrintTSM(M);return 0;
}
效果演示:
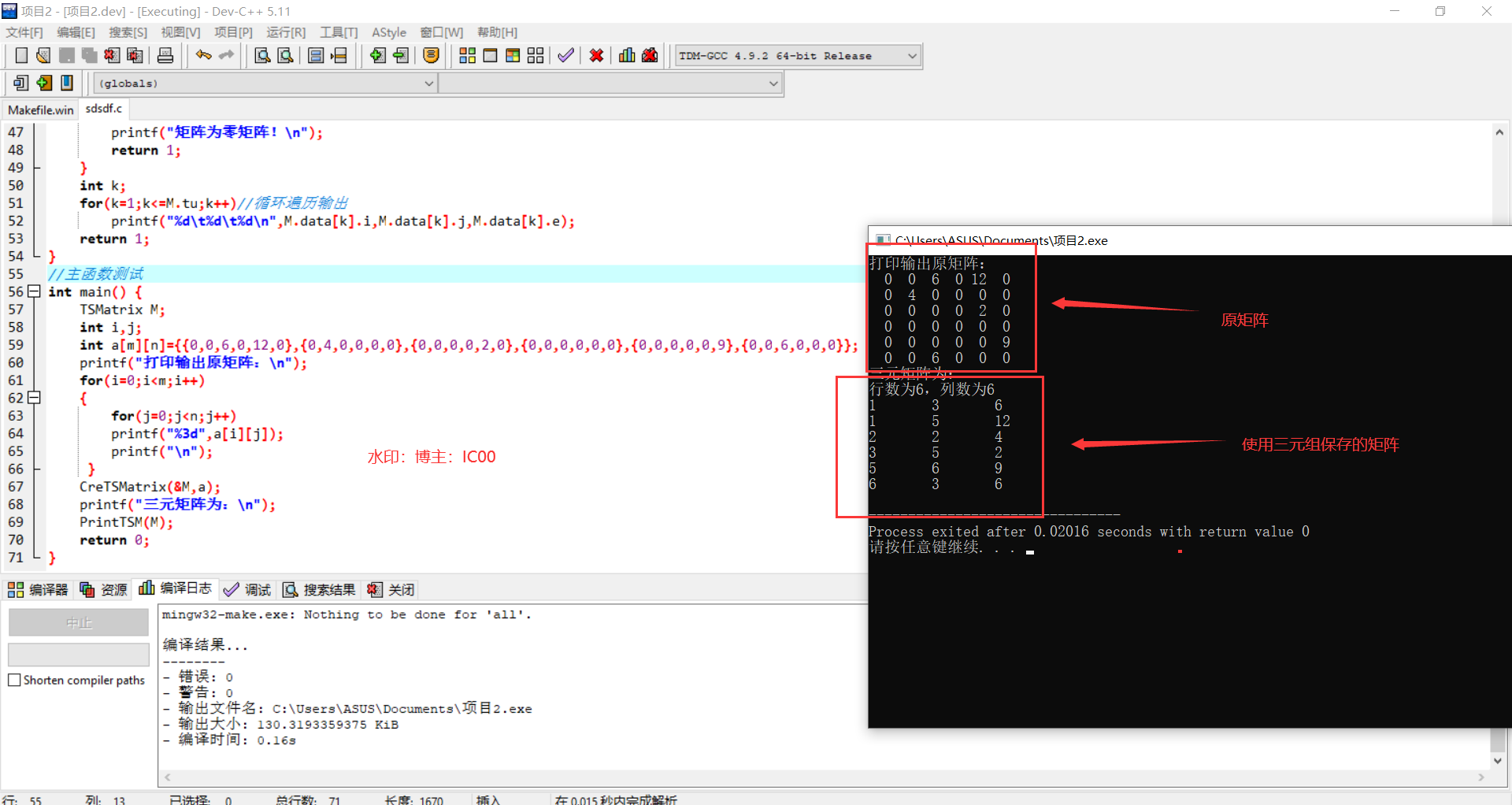
注:三元组顺序表缺点是:不能随机存取,若按行号存取莫一行的非零元素,则需要从头开始查找,十字链克服了这个缺点。
3.简单逻辑稀疏矩阵的十字链表示
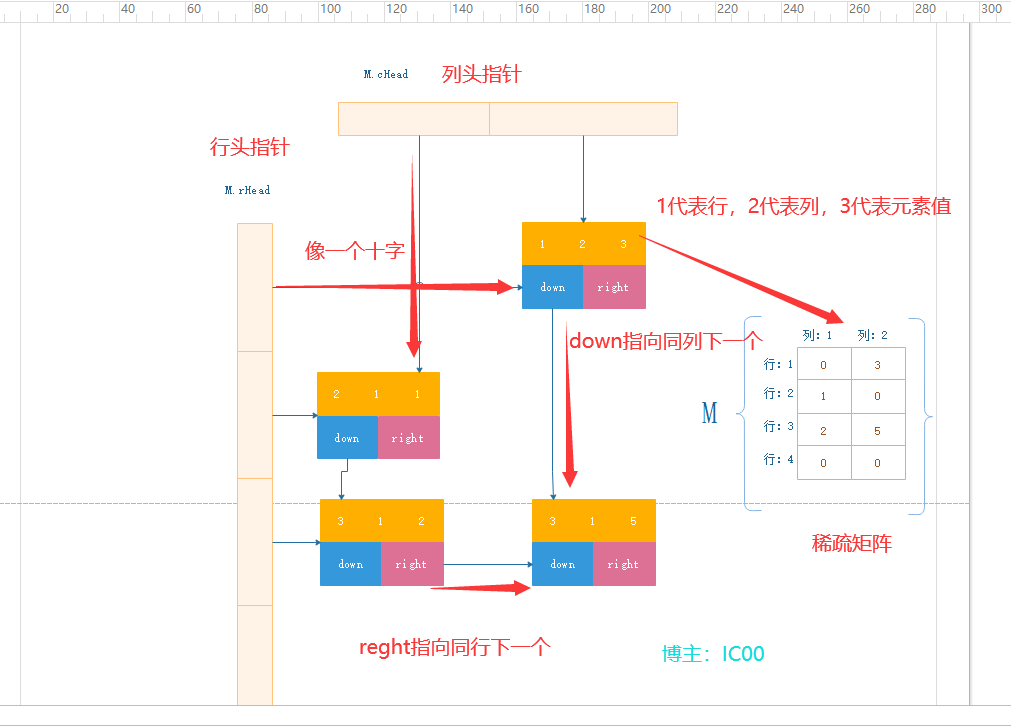
十字链它能够灵活地插入因运算而产生的新的非零元素,删除因运算而产生的新的零元素,实现矩阵的各种运算。在十字链表中,矩阵的每一个非零元素用一个结点表示,该结点除了(行、行、值)以外,还要有两个域:(right:用于链接同一行中的下一个非零元素; down:用以链接同一列中的下一个非零元素。),画一个结点图给大家看一下:
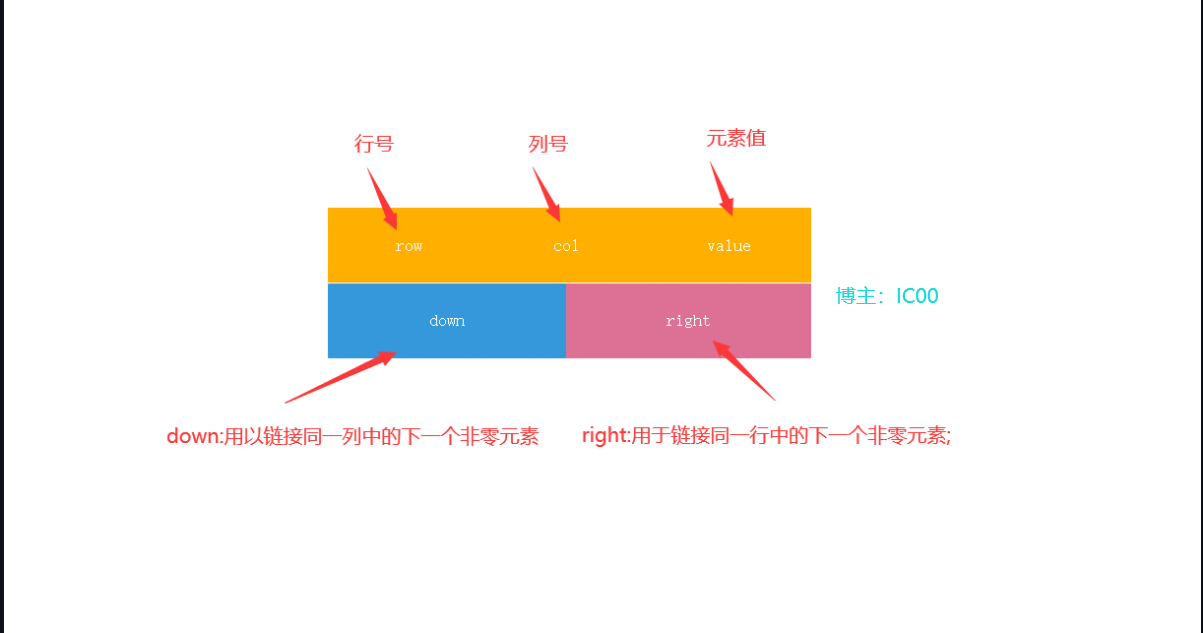
十字链连接逻辑图:
typedef struct node { int row,col; //行号与列号 int value; //值 struct OLNode *right, *down; //同行、同列下一个元素的指针
}node, *List;
typedef struct{List *rhead, *chead; //行和列链表头指针向量基址int mu,nu,tu; //稀疏矩阵的行数,列数和非零元个数
}HeadList;
由于时间关系博主具体实现代码就不往后写了,具体实现逻辑就是把每一行每一列看作是一个链表的结点,两条链表,一条是行,一条是列,这一条上面的结点就代表数组的一行一列,或者理解为行号和列号,然后,里面有个node结构体就是我们要放的值。有机会博主写出来,把具体实现和一些十字链的操作单独写一篇文章,而学数据结构,了解就可以了,考试一般不会考,考了,看了博主这个逻辑,也不会说完全不会。有时间博主出一篇专门讲稀疏矩阵的十字链。
总结:
数组的章节我们就差不多完全学完了,其实也不怎么难,我们需要耐心去学习,博主在学文章,也会看很多视频,资料,敲代码,但是我自己学了那么久了,真的感觉学任何东西,逻辑一定要学懂,就算你写不出来,考试了,只要你会逻辑会语言,也不至于完全看不懂,最起码,你可以看懂,你不会逻辑你看都看不懂。创作不易点赞,关注,评论,收藏。
上一篇:数据结构专升本学习,数组和数组矩阵的三种压缩(画图教你矩阵对称,对角压缩,三角压缩)
下一篇:数据结构专升本学习,树篇(一张图教会你,树结点的关系,画图教你树的四种表示法(树状,文氏图标,凹入表示法,括号表示法),三种遍历(先根,后根层次遍历))

这篇关于三元组和十字链,稀疏矩阵(画图教你稀疏矩阵的三元组和十字链表示)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!