基于jupyter notebook的python编程-----通过python编程实现通信系统的多径仿真

一、多径衰落信道简介

1、多径衰落信道

在无线信道中，发送和接收天线之间通常存在多于一条的信号传播路径。多径的存在是因为发射机和接收机之间建筑物和其他物体的反射、绕射、散射等引起的。当信号在无线信道传播时，多径反射和衰减的变化将使信号经历随机波动。因此，无线信道的特性是不确定的、随机变化的。

2、多径衰落信道特点

• 频率选择性衰落
• 时间选择性衰落

3、多径衰落信道原理

本次博客，通过一个简单的模拟程序来说明多径衰落信道的特点，然后再给出多径衰落信道的仿真方法。
1）、首先，先说一下程序模拟多径信道的场景，如图4-15所示

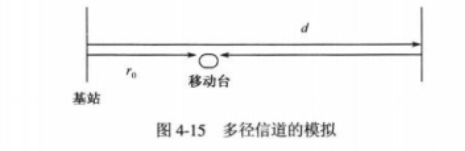
假设在一条笔直的高速公路上，一端安装了一个固定的基站，在另一端有一面完全反射电磁波的墙面，基站距反射墙的距离为d，移动台距基站初始距离为$r_0$。基站发射一个频率为f的正弦信号，表示为$cos(2\pi ft)$，由于墙面的反射，移动台可以接收到2径信号，其中之一是从基站直接发射的信号，另一径是从反射墙反射过来的信号。
2）、首先来看移动台静止的情况。显然，从基站发出的直射信号到达移动台需要的时间为 $r_0/c$ (c为光速)，从反射墙反射过来的信号到达移动台所需要的时间为 $(2d-r_0)/c$。换句话说，在时
刻t,移动台分别接收到了从时刻 $t-r_0/c$ 基站发出的直射信号和从时刻 $t-((2d-r_0)/c)$ 基站发出的反射信号。
3）、信号在传播的过程中要衰减，自由空间中，电磁波功率随距离r按平方规律衰减，相应的电场强度(接收信号电压)随 $1/r$ 规律衰减并且反射信号同直射信号的相位相反。所以，时刻t移动台接收到的合成信号为

式中，减号体现了反射信号与直射信号的相位相反

接下来，我们就通过python代码来实现上面的原理吧！

二、python的多径衰落信道模拟

1、在$r_0$处的信道特点

1）、python代码如下所示：

#r0=3
import numpy as np
from numpy import random
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei'] #显示中文标签
plt.rcParams['axes.unicode_minus']=False
f=1                                        #发射信号频率
v=0                                        #移动台速度，静止时刻为0
c=3e8                                      #电磁波速度，光速
r0=3                                       #移动台距离基站的初始距离
d=10                                       #基站距离反射墙的距离
t1=np.array([])                            #时间
for i in np.arange(0.1,10+0.0001,0.0001):t1=np.insert(t1,len(t1),i)
E1=np.cos(2*np.pi*f*((1-v/c)*t1-r0/c))/(r0+v*t1)                 #直射径信号
E2=np.cos(2*np.pi*f*((1+v/c)*t1+(r0-2*d)/c))/(2*d-r0-v*t1)      #反射径信号
plt.plot(t1,E1,t1,E2,'-g',t1,E1-E2,'-r')                          #画出直射径信号、反射径信号、移动台接收的合成信号
plt.legend(["直射径信号","反射径信号","移动台接收的合成信号"],loc='upper left')
plt.axis([0,10,-0.8,0.8])                                         #设置横纵比
plt.show()

2）、模拟结果

3）、结论
上图可以清楚地看出，即使移动台是静止的，由于反射径的存在，使得接收到的合成信号最大值要小于直射径的信号.

2、修改移动台距离基站的位置，让$r_0=9$

1）、python代码如下所示：

#r0=9
f=1                                        #发射信号频率
v=0                                        #移动台速度，静止时刻为0
c=3e8                                      #电磁波速度，光速
r0=9                                       #移动台距离基站的初始距离
d=10                                       #基站距离反射墙的距离
t1=np.array([])                            #时间
for i in np.arange(0.1,10+0.0001,0.0001):t1=np.insert(t1,len(t1),i)
E1=np.cos(2*np.pi*f*((1-v/c)*t1-r0/c))/(r0+v*t1)                 #直射径信号
E2=np.cos(2*np.pi*f*((1+v/c)*t1+(r0-2*d)/c))/(2*d-r0-v*t1)      #反射径信号
plt.plot(t1,E1,t1,E2,'-g',t1,E1-E2,'-r')                          #画出直射径信号、反射径信号、移动台接收的合成信号
plt.legend(["直射径信号","反射径信号","移动台接收的合成信号"],loc='upper left')
plt.axis([0,10,-0.8,0.8])                                         #设置横纵比
plt.show()

2）、模拟结果

3）、结论
从图中可以看出，这次由于靠近反射墙的位置，直射信号要比$r_0=3$处弱-一些，反射信号要比$r_0=3$位置处的信号强一些，但移动台接收到的合成信号更弱了，不仅要小于直射径的信号更小于反射径的信号

3、修改发射频率$f=10^8且r_0=3$

以上是发射频率f=1的情况，发射其他频率的信号结果会怎样呢?修改$f=10^8$并且$r_0=3$
1）、python代码如下所示：

#f=10的8次方，r0=3
f=1e8                                      #发射信号频率
v=0                                        #移动台速度，静止时刻为0
c=3e8                                      #电磁波速度，光速
r0=3                                       #移动台距离基站的初始距离
d=10                                       #基站距离反射墙的距离
t1=np.array([])                            #时间
for i in np.arange(0.1,10+0.0001,0.0001):t1=np.insert(t1,len(t1),i)
E1=np.cos(2*np.pi*f*((1-v/c)*t1-r0/c))/(r0+v*t1)                 #直射径信号
E2=np.cos(2*np.pi*f*((1+v/c)*t1+(r0-2*d)/c))/(2*d-r0-v*t1)      #反射径信号
plt.plot(t1,E1,t1,E2,'-g',t1,E1-E2,'-r')                          #画出直射径信号、反射径信号、移动台接收的合成信号
plt.legend(["直射径信号","反射径信号","移动台接收的合成信号"],loc='upper left')
plt.axis([0,10,-0.8,0.8])                                         #设置横纵比
plt.show()

2）、模拟结果

3）、结论
我们会发现，此时移动台接收到的信号得到了增强；至此，可以得出结论，在同一位置， 由于反射径信号的存在，发射不同频率的信号时，在接收机处接收到信号有的频率是被增强了，有的频率是被削弱了。频率选择性衰落由此产生。
4）、扩展
既然有频率选择性衰落，自然会问，哪些频率会被增强，哪些频率会被削弱呢?在上面的例子中，如果f=1, 2, 3，.100, … 1000， 会发现这些频率基本，上都是被削弱的，只有让f充分大，如f=10", 才会看出信号被增强了，那么就把那些受到影响基本一致的频率范围称为相干带宽。

4、让移动台以速度v=1向反射墙运动

使$f=2,v=1,r0=3,d=15,t1=0.1:12:0.001$

1）、上面讨论 了移动台静止的情况。现在让移动台向反射墙运动，速度为v，则在时刻t,移动台距离基站的位置r=r+vt。把最开始式中的$r_0$用r代替得：

2）、那么通过python代码模拟如下：

#f=2,v=1,r0=3，d=15,t1=0.1:12:0.001 
f=2                                        #发射信号频率
v=1                                        #移动台速度，静止时刻为0
c=3e8                                      #电磁波速度，光速
r0=3                                       #移动台距离基站的初始距离
d=15                                       #基站距离反射墙的距离
t1=np.array([])                            #时间
for i in np.arange(0.1,12+0.001,0.001):t1=np.insert(t1,len(t1),i)
E1=np.cos(2*np.pi*f*((1-v/c)*t1-r0/c))/(r0+v*t1)                 #直射径信号
E2=np.cos(2*np.pi*f*((1+v/c)*t1+(r0-2*d)/c))/(2*d-r0-v*t1)      #反射径信号
plt.plot(t1,E1,t1,E2,'-g',t1,E1-E2,'-r')                          #画出直射径信号、反射径信号、移动台接收的合成信号
plt.legend(["直射径信号","反射径信号","移动台接收的合成信号"],loc='upper left')
plt.axis([0,12,-0.5,0.5])                                         #设置横纵比
plt.show()

3）、模拟结果：

5、分离出移动台接收的合成信号

1）、分离接收合成信号python代码如下所示：

#f=2,v=1,r0=3，t1=0.1:12:0.001时候单独画接收信号
f=2                                        #发射信号频率
v=1                                        #移动台速度，静止时刻为0
c=3e8                                      #电磁波速度，光速
r0=3                                       #移动台距离基站的初始距离
d=15                                       #基站距离反射墙的距离
t1=np.array([])                            #时间
for i in np.arange(0.1,12+0.001,0.001):t1=np.insert(t1,len(t1),i)
E1=np.cos(2*np.pi*f*((1-v/c)*t1-r0/c))/(r0+v*t1)                 #直射径信号
E2=np.cos(2*np.pi*f*((1+v/c)*t1+(r0-2*d)/c))/(2*d-r0-v*t1)      #反射径信号
plt.plot(t1,E1-E2,'-r')                                           #移动台接收的合成信号
plt.legend(["移动台接收的合成信号"],loc='upper left')
plt.axis([0,12,-0.5,0.5])                                         #设置横纵比
plt.show()

2）、分离结果：

3）、结论
从前面的程序中可知多径导致了频率选择性。当移动台运动起来后，发现即使同一频率，在不同的时间点，合成信号的强度也是不一样的。

三、多径仿真结论

1、多径仿真结论

1）、在数字通信中，接收端是周期性的对接收符号进行判决从而恢复信息的，1个符号脉冲的周期可大可小，因此，根据相干时间与符号脉冲周期的相对长短，可以把信道分为慢变信道和快变信道。在上面第二张图中，如果发送符号的周期小于1.25s,就可以认为这是慢变信道(或者准静态信道）
2）、无线信道大体可以分为4种：慢变瑞利衰落信道、快变瑞利衰落信道、慢变频率选择性信道、快变频率选择性信道。

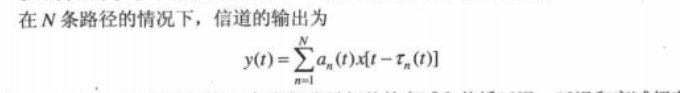
2、多径扩展

1）、如果信道没有频率选择性，则最大的时延扩展Tmax要远远小于符号周期T(Tmax <<T,)，在这种情况下，所有的延迟多径分量到达的时段仅为一个符号时间的一小部分。 在这种情况下，信道可以用单一路径来建模，输入/输出关系可以表示为乘法，即：

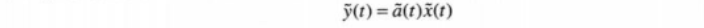
四、Matlab多径仿真完整代码

林君学长同时在这里给出Matlab的多径仿真的一部分代码，其他可通过以下代码改写

1、matlab多径源码如下

clear all
f=1;        %发射信号频率
v=0;        %移动台速度，静止时刻为0
c=3e8;      %电磁波速度，光速
r0=3;       %移动台距离基站的初始距离
d=10;       %基站距离反射墙的距离
t1=0.1:0.0001:10;     %时间
E1=cos(2*pi*f*((1-v/c).*t1-r0/c))./(r0+v.*t1);    %直射径信号
E2=cos(2*pi*f*((1+v/c)*t1+(r0-2*d)/c))./(2*d-r0-v*t1);  %反射径信号
figure
plot(t1,E1,t1,E2,'-g',t1,E1-E2,'-r')   %移动台接收的合成信号
legend('直射径信号','反射径信号','移动台接收的合成信号')
axis([0 10 -0.8 0.8])     %设置横纵比

以上就是本次博客的全部内容啦，通过本次博客，大家可以更好的了解到通信系统多径仿真原理，同时，林君学长也希望大家能够深入的了解多径衰落应该如何降低到最低，适合我们信号传输的那个点，理解原理；代码有错误的地方记得给林君学长留言改正。
遇到问题的小伙伴也记得评论区留言，林君学长看到会给大家回复解答的，这个学长不太冷！
陈一月的又一天编程岁月^ _ ^