WebGL模型拾取——射线法

2024-01-20 15:40
文章标签 模型 webgl 拾取 射线

本文主要是介绍WebGL模型拾取——射线法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

　　今天要把WebGL中一个非常重要的算法记录下来——raycaster射线法拾取模型。首先我们来了解一下为什么要做模型拾取，我们在做webgl场景交互的时候经常要选中场景中的某个模型，比如鼠标拖拽旋转，平移。为了能做到鼠标交互，就首先要能选中场景中的模型对象，这就要用到模型拾取算法，本文仅讨论射线法模型拾取raycaster。

　　所谓射线法就是利用一根射线去和场景中的模型进行碰撞，撞到的模型对象就是被拾取到的模型。请看下图

　　我逐个来解释一下上图中的元素。首先解释相机（camera），这就是人眼的抽象，代表用户在屏幕前的眼睛位置。人眼看到的世界是透视的（perspective），因此我们构造的视棱台（frustum）基于透视投影。整个视棱台区域介于场景近截面（near）和远截面（far）之间，这个区间内的空间就是我们可以看到的场景空间。需要说明一下，near近截面我们这里紧贴屏幕（screen），即距离很小约等于0.1，far远截面就是我们认为的视线最远能看到的距离，我们这里设置为1000。屏幕screen在近截面前0.1的位置上，也是离人眼最近的截面，也是鼠标交互的界面，这是要事先解释明白的。理解了这个空间结构以后我们就开始讲解raycaster的算法原理。

　　首先我们来看一下鼠标在屏幕上的位置点P0，我们可以看到P0点（鼠标），这个就是鼠标在屏幕上的位置。我们再来看看triangle1三角形1，这就是透视空间中triangle2三角形2在屏幕上的投影。我们可以明显看到鼠标位置P0点在屏幕triangle1三角形1内部，即鼠标点选中triangle1三角形1。这在屏幕上可以看的很清楚，但是问题来了，在空间中鼠标是没有深度概念的，即鼠标只有XY坐标，没有Z坐标，那我们在视棱台的空间坐标系中如何表示鼠标的三维空间位置呢，如果没有鼠标的3维空间坐标，如何判断在视棱台空间中鼠标是否选中triangle2三角形2这个模型对象呢？也许有同学会说，triangle1就是triangle2的投影嘛，选中投影就是选中模型了不是，我就这么说，非常正确，能说出这样的话就已经完全理解了模型在屏幕上的投影的原理，但是新的问题随之又来了，如何获取鼠标点选模型的坐标呢，即如何得到鼠标点在模型上的那个点的三维空间坐标呢，如果仅仅判断是否选中，那投影就够用了，但要计算鼠标点选模型上的点坐标，就远远不够用了。为了解决这个问题，raycaster算法应运而生。

　　raycaster顾名思义就是射线投射。他的原理其实非常简单，就是用一根射线去交有限平面，获得交点。射线是有起点的，起点就是我们的眼睛。我们做一根起于camera，通过鼠标在屏幕上的位置P0，继续延伸，交视棱台近截面于P1，继续延伸，交视棱台远截面于P3，射线截止，我们得到了一根线段P1-P3。这根线段P1-P3就是我们眼睛能看到的鼠标发出的射线在透视空间中的部分，凡是这根线段碰到的模型，都是鼠标点选中的空间模型。而这根线段和模型的交点就是鼠标点选模型的交点，这个交点坐标就是鼠标点选模型的交点空间三维坐标。这样就顺利解决了上面我们的问题，即求鼠标点选空间三维模型的交点坐标。在上图中我们看得很清楚，这个交点就是P2，接下来我们就来讲解怎么求这个P2的空间坐标。

　　做图形学的同学们都非常清楚。如何求线段和平面的交点，这里我截取一部分代码，以供叙述方便，以下就是求线段截取平面交点的函数。

/**/
let Intersector = require('./Intersector');
let LineSegmentIntersection = require('./Intersection').LineSegmentIntersection;
let Vec3 = require('./Vec3');
let Mat4 = require('./Mat4');
let Algorithm = require('./Algorithm');let LineSegmentIntersector = function () {Intersector.call(this);//原始的起始点和临界值，初始化设置的数据，保留作为参照，设置后不再变动this._orginStart = Vec3.new();//线段起点this._orginEnd = Vec3.new();//线段终点this._orginThreshold = 0.0;//点和线求相交时的临界值，完全相交是很难求到的//临时存储，每次求交都可能会变动的数据//对于有变换的几何求交，不会变换几何顶点而是变换起始点和临界值this._start = Vec3.new();//线段起点this._end = Vec3.new();//线段终点this._threshold = 0.0;//点和线求相交时的临界值，完全相交是很难求到的this._direction = Vec3.new();this._length = 0;this._inverseLength = 0;this._matrix = Mat4.new();
};LineSegmentIntersector.prototype = Object.create(Intersector.prototype);
LineSegmentIntersector.prototype.constructor = LineSegmentIntersector;
Object.assign(LineSegmentIntersector.prototype, {init: function (start, end, threshold) {Vec3.copy(this._orginStart, start);Vec3.copy(this._orginEnd, end);Vec3.copy(this._start, start);Vec3.copy(this._end, end);if (threshold !== undefined) {this._orginThreshold = threshold;this._threshold = threshold;}},intersect: function (drawable) {//先使用包围盒子if (!drawable.getBoundingBox().intersectLineSegment(this._orginStart, this._orginEnd)) {return;}this._drawable = drawable;let geometry = drawable.getGeometry();let vertexbuffer = geometry.getBufferArray('Vertex');this._vertices = vertexbuffer.getArrayBuffer();//没有顶点数据不处理直接返回if (!this._vertices) return;//没有图元不处理直接返回let primitive = geometry.getPrimitive();if (!primitive) return;//初始化求相交的各种数据let matrix = drawable.getTransform();if (this._transform !== matrix) {//如果不一样，需要计算新的起始点以及各种临时数据this._transform = matrix;Mat4.invert(this._matrix, matrix);//根据矩阵计算新的临界值if (this._orginThreshold > 0.0) {let tmp = this._start;Mat4.getScale(tmp, this._matrix);let x = tmp[0];let y = tmp[1];let z = tmp[2];this._threshold = this._orginThreshold * (x > y ? (x > z ? x : z) : y > z ? y : z);}//根据矩阵计算新的起始点Vec3.transformMat4(this._start, this._orginStart, this._matrix);Vec3.transformMat4(this._end, this._orginEnd, this._matrix);//根据新的起始点计算各种临时数据Vec3.sub(this._direction, this._end, this._start);this._length = Vec3.length(this._direction);//长度this._inverseLength = this._length <= Algorithm.EPSILON ? 0.0 : 1.0 / this._length;Vec3.scale(this._direction, this._direction, this._inverseLength);//求单位向量}//如果变换与上次一样，直接使用上次的数据求相交//求相交primitive.operate(this);},intersectPoint: function (vertex) {// https://www.geometrictools.com/GTEngine/Include/Mathematics/GteDistPointSegment.h//起点指向绘制点，向量Mlet m = Vec3.MemoryPool.alloc();Vec3.sub(m, vertex, this._start);//起点指向终点，向量Nlet n = Vec3.MemoryPool.alloc();Vec3.sub(n, this._end, this._start);//求M在N上的投影比例值//|m|*|n|*cos / \n\*\n\ = |m|*cos/\n\let r = Vec3.dot(m, n) * this._inverseLength * this._inverseLength;//计算绘制点到线段的距离let sqrdist = 1.0;if (r < 0.0) {//夹角超过90度，绘制点在当前线段起点后面，求绘制点与起点的距离sqrdist = Vec3.sqrLen(m);} else if (r > 1.0) {//绘制点在当前线段终点后面，求绘制点与终点的距离sqrdist = Vec3.sqrDist(vertex, this._end);} else {//在0到1之间//m - n * r 如果平行或者接近于平行，结果接近于0，相交sqrdist = Vec3.sqrLen(Vec3.scaleAndAdd(m, m, n, -r));}let intersection = undefined;if (sqrdist > this._threshold * this._threshold) {//超过了临界值，没有相交返回
} else {//相交intersection = new LineSegmentIntersection();//intersection._i1 = index;//intersection._r1 = 1.0;Vec3.scaleAndAdd(intersection._point, this._start, n, r);intersection._ratio = r;}Vec3.MemoryPool.free(m);Vec3.MemoryPool.free(n);return intersection;},intersectLine: function (vertex0, vertex1) {// https://www.geometrictools.com/GTEngine/Samples/Geometrics/DistanceSegments3/DistanceSegments3.cpp//let epsilon = 0.00000001;//起点到终点的向量let u = Vec3.MemoryPool.alloc();Vec3.sub(u, vertex1, vertex0);let v = Vec3.MemoryPool.alloc();Vec3.sub(v, this._end, this._start);let w = Vec3.MemoryPool.alloc();Vec3.sub(w, vertex0, this._start);let a = Vec3.dot(u, u);let b = Vec3.dot(u, v);let c = Vec3.dot(v, v);let d = Vec3.dot(u, w);let e = Vec3.dot(v, w);let D = a * c - b * b;let sN;let tN;let sD = D;let tD = D;// compute the line parameters of the two closest pointsif (D < Algorithm.EPSILON) {//平行// the lines are almost parallelsN = 0.0; // force using point P0 on segment S1sD = 1.0; // to prevent possible division by 0.0 latertN = e;tD = c;} else {// get the closest points on the infinite linessN = b * e - c * d;tN = a * e - b * d;if (sN < 0.0) {// sc < 0 => the s=0 edge is visiblesN = 0.0;tN = e;tD = c;} else if (sN > sD) {// sc > 1  => the s=1 edge is visiblesN = sD;tN = e + b;tD = c;}}if (tN < 0.0) {// tc < 0 => the t=0 edge is visibletN = 0.0;// recompute sc for this edgeif (-d < 0.0) sN = 0.0;else if (-d > a) sN = sD;else {sN = -d;sD = a;}} else if (tN > tD) {// tc > 1  => the t=1 edge is visibletN = tD;// recompute sc for this edgeif (-d + b < 0.0) sN = 0;else if (-d + b > a) sN = sD;else {sN = -d + b;sD = a;}}// finally do the division to get sc and tclet sc = Math.abs(sN) < Algorithm.EPSILON ? 0.0 : sN / sD;let tc = Math.abs(tN) < Algorithm.EPSILON ? 0.0 : tN / tD;// get the difference of the two closest pointslet closest0 = Vec3.MemoryPool.alloc();let closest1 = Vec3.MemoryPool.alloc();Vec3.scaleAndAdd(closest0, vertex0, u, sc);Vec3.scaleAndAdd(closest1, this._start, v, tc);let sqrDistance = Vec3.sqrDist(closest0, closest1);Vec3.MemoryPool.free(closest0);Vec3.MemoryPool.free(closest1);let intersection = undefined;if (sqrDistance > this._threshold * this._threshold) {} else {//相交intersection = new LineSegmentIntersection();// intersection._i1 = index0;// intersection._i2 = index1;// intersection._r1 = 1.0 - tc;// intersection._r2 = tc;
            Vec3.copy(intersection._point, closest1);intersection._ratio = tc;}Vec3.MemoryPool.free(u);Vec3.MemoryPool.free(v);Vec3.MemoryPool.free(w);return intersection;},intersectTriangle: function (vertex0, vertex1, vertex2) {let e2 = Vec3.MemoryPool.alloc();Vec3.sub(e2, vertex2, vertex0);let e1 = Vec3.MemoryPool.alloc();Vec3.sub(e1, vertex1, vertex0);let pvec = Vec3.MemoryPool.alloc();Vec3.cross(pvec, this._direction, e2);let intersection = undefined;//线段与三角面点积let det = Vec3.dot(pvec, e1);//判断三角形所在的平面与线段是否平行，如果平行铁定不相交，面片没有厚度if (Math.abs(det) < Algorithm.EPSILON) {//return undefined;}else{let invDet = 1.0 / det;let tvec = Vec3.MemoryPool.alloc();Vec3.sub(tvec, this._start, vertex0);let u = Vec3.dot(pvec, tvec) * invDet;//三角面超出了线段两个点范围外面，铁定不相交if (u < 0.0 || u > 1.0) {//return undefined;}else{let qvec = Vec3.MemoryPool.alloc();Vec3.cross(qvec, tvec, e1);let v = Vec3.dot(qvec, this._direction) * invDet;//
                if (v < 0.0 || u + v > 1.0) {//return undefined;}else{let t = Vec3.dot(qvec, e2) * invDet;if (t < Algorithm.EPSILON || t > this._length) {//return undefined;}else{//相交intersection = new LineSegmentIntersection();//求相交点let r0 = 1.0 - u - v;let r1 = u;let r2 = v;let r = t * this._inverseLength;let interX = vertex0[0] * r0 + vertex1[0] * r1 + vertex2[0] * r2;let interY = vertex0[1] * r0 + vertex1[1] * r1 + vertex2[1] * r2;let interZ = vertex0[2] * r0 + vertex1[2] * r1 + vertex2[2] * r2;// intersection._i1 = index0;// intersection._i2 = index1;// intersection._i3 = index2;// intersection._r1 = r0;// intersection._r2 = r1;// intersection._r3 = r2;//这里的点没有经过变换，不是真实的世界坐标点Vec3.set(intersection._point, interX, interY, interZ);Vec3.transformMat4(intersection._point, intersection._point, this._transform);//求法向量，法向量未变换，如果有用途也要变换let normal = intersection._normal;Vec3.cross(normal, e1, e2);Vec3.normalize(normal, normal);//比例，在相交线段上的比例，不需要变换intersection._ratio = r;}}Vec3.MemoryPool.free(qvec);}Vec3.MemoryPool.free(tvec);}Vec3.MemoryPool.free(e1);Vec3.MemoryPool.free(e2);Vec3.MemoryPool.free(pvec);return intersection;// http://gamedev.stackexchange.com/questions/54505/negative-scale-in-matrix-4x4// https://en.wikipedia.org/wiki/Determinant#Orientation_of_a_basis// you can't exactly extract scale of a matrix but the determinant will tell you// if the orientation is preserved//intersection._backface = mat4.determinant(intersection._matrix) * det < 0;
    },intersectBoundingBox: function (box) {return box.intersectLineSegment(this._orginStart, this._orginEnd);},
});module.exports = LineSegmentIntersector;// setDrawable: function (drawable) {
//     this._geometry = drawable.getGeometry();
//     this._vertices = this._geometry.getBufferArray('Vertex');
//
//     let matrix = drawable.getTransform();
//     if (this._transform === matrix) {//如果与上次的一样，不再处理
//         return;
//     }
//
//     //如果不一样，需要计算新的起始点已经各种临时数据
//     this._transform = matrix;
//     Mat4.invert(this._matrix, matrix);
//
//     //根据矩阵计算新的临界值
//     if (this._orginThreshold > 0.0) {
//         let tmp = this._start;
//         Mat4.getScale(tmp, this._matrix);
//         let x = tmp[0];
//         let y = tmp[1];
//         let z = tmp[2];
//         this._threshold = this._orginThreshold * (x > y ? (x > z ? x : z) : y > z ? y : z);
//     }
//     //根据矩阵计算新的起始点
//     Vec3.transformMat4(this._start, this._orginStart, this._matrix);
//     Vec3.transformMat4(this._end, this._orginEnd, this._matrix);
//
//     //根据新的起始点计算各种临时数据
//     Vec3.sub(this._direction, this._end, this._start);
//     this._length = Vec3.length(this._direction);//长度
//     this._inverseLength = this._length <= Algorithm.EPSILON ? 1.0 / this._length : 0.0;
//     Vec3.scale(this._direction, this._direction, this._inverseLength);//求单位向量
// },
// setGeometry: function (geometry, matrix) {
//     Intersector.prototype.setGeometry.call(this, geometry, matrix);
//
//     //如果不一样，需要计算新的起始点已经各种临时数据
//     Mat4.invert(this._matrix, matrix);
//
//     //根据矩阵计算新的临界值
//     if (this._orginThreshold > 0.0) {
//         let tmp = this._start;
//         Mat4.getScale(tmp, this._matrix);
//         let x = tmp[0];
//         let y = tmp[1];
//         let z = tmp[2];
//         this._threshold = this._orginThreshold * (x > y ? (x > z ? x : z) : y > z ? y : z);
//     }
//     //根据矩阵计算新的起始点
//     Vec3.transformMat4(this._start, this._orginStart, this._matrix);
//     Vec3.transformMat4(this._end, this._orginEnd, this._matrix);
//
//     //根据新的起始点计算各种临时数据
//     Vec3.sub(this._direction, this._end, this._start);
//     this._length = Vec3.length(this._direction);//长度
//     this._inverseLength = this._length <= Algorithm.EPSILON ? 1.0 / this._length : 0.0;
//     Vec3.scale(this._direction, this._direction, this._inverseLength);//求单位向量
// },
// setGeometry: function (geometry) {
//     //没有顶点数据不处理直接返回
//     let vertexbuffer = geometry.getBufferArray('Vertex');
//     if(!vertexbuffer) return;
//
//     //没有图元不处理直接返回
//     let primitive = geometry.getPrimitive();
//     if (primitive)
//         primitive.operate(this);
// },

　　以上的LineSegmentIntersector就是计算线段和平面交点的类，具体算法不再赘述，请自行参考《WebGL编程指南》。好了，我们接下来就看一个项目中的具体案例，请看下图

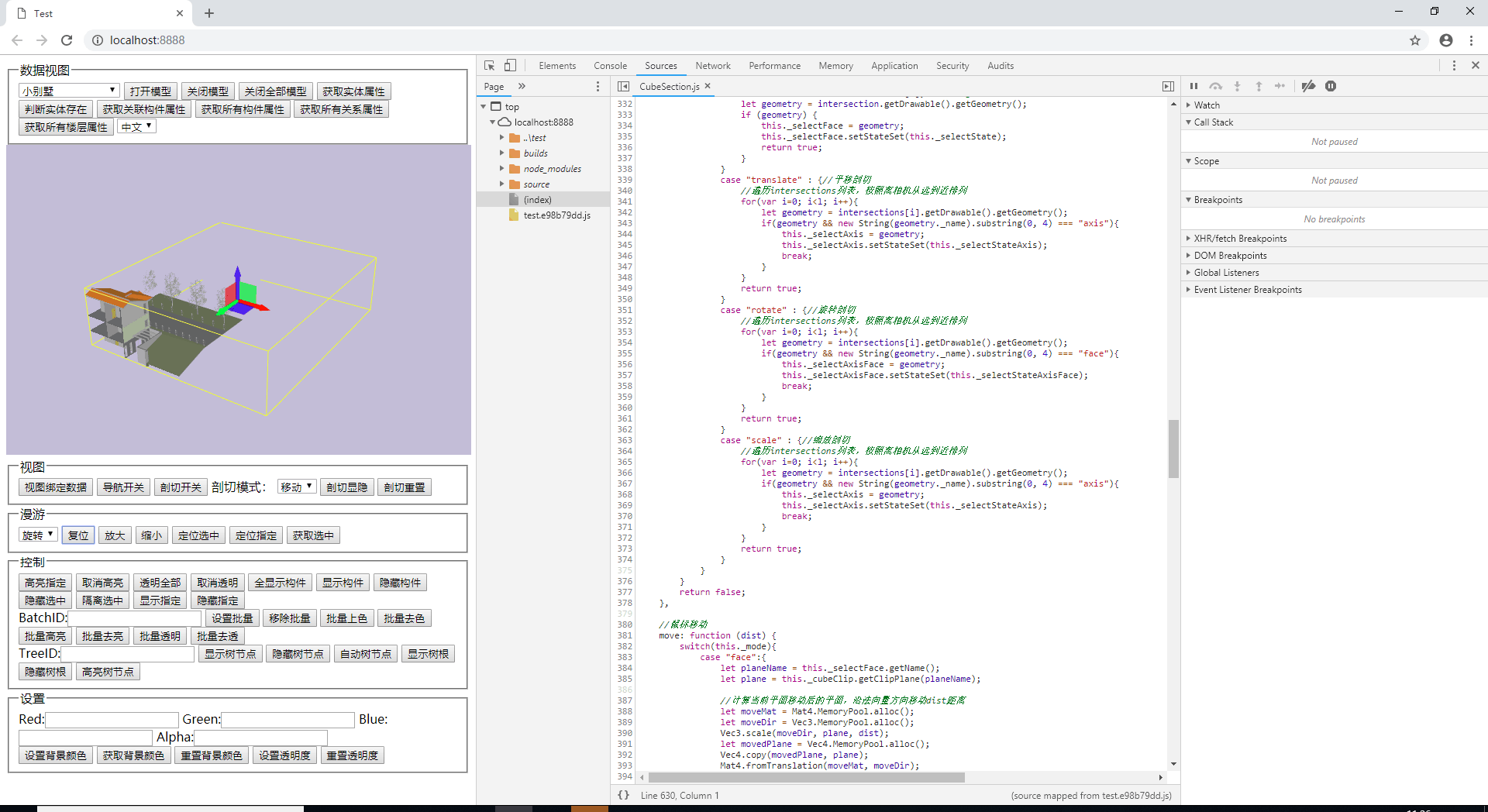
　　我们在pick事件中使用了LineSegmentIntersector对场景中的包围盒和坐标系模型进行了raycaster射线碰撞检测，结果我们得到了一系列的返回对象，其中包括包围盒的2个面，坐标系的一根坐标轴的geometry，这就另我们觉得难办了，鼠标射线碰到了不止一个模型，我们该怎么办呢，这里就要说明一下，一般我们都取离near近截面最近的一个模型作为我们pick选中的模型，因为其他模型都被处于前方的该模型遮挡住了。

　　好了，今天对raycaster的解释就结束了，只是初步了解一下，raycaster还有很多应用场景，这里和我们的鼠标拾取不相关的就不介绍了，谢谢大家阅读，欢迎大家一起留言探讨，再次感谢。转载本文请注明出处：https://www.cnblogs.com/ccentry/p/9973165.html

这篇关于WebGL模型拾取——射线法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/626506。

相关文章

Python基于火山引擎豆包大模型搭建QQ机器人详细教程(2024年最新)

Python基于火山引擎豆包大模型搭建QQ机器人详细教程(2024年最新)

《Python基于火山引擎豆包大模型搭建QQ机器人详细教程(2024年最新)》：本文主要介绍Python基于火山引擎豆包大模型搭建QQ机器人详细的相关资料,包括开通模型、配置APIKEY鉴权和SD... 目录豆包大模型概述开通模型付费安装 SDK 环境配置 API KEY 鉴权Ark 模型接口Prompt
阅读更多...
大模型研发全揭秘：客服工单数据标注的完整攻略

大模型研发全揭秘：客服工单数据标注的完整攻略

在人工智能（AI）领域，数据标注是模型训练过程中至关重要的一步。无论你是新手还是有经验的从业者，掌握数据标注的技术细节和常见问题的解决方案都能为你的AI项目增添不少价值。在电信运营商的客服系统中，工单数据是客户问题和解决方案的重要记录。通过对这些工单数据进行有效标注，不仅能够帮助提升客服自动化系统的智能化水平，还能优化客户服务流程，提高客户满意度。本文将详细介绍如何在电信运营商客服工单的背景下进行
阅读更多...
Andrej Karpathy最新采访：认知核心模型10亿参数就够了，AI会打破教育不公的僵局

Andrej Karpathy最新采访：认知核心模型10亿参数就够了，AI会打破教育不公的僵局

夕小瑶科技说 原创  作者 | 海野 AI圈子的红人，AI大神Andrej Karpathy，曾是OpenAI联合创始人之一，特斯拉AI总监。上一次的动态是官宣创办一家名为 Eureka Labs 的人工智能+教育公司 ，宣布将长期致力于AI原生教育。 近日，Andrej Karpathy接受了No Priors（投资博客）的采访，与硅谷知名投资人 Sara Guo 和 Elad G
阅读更多...
Retrieval-based-Voice-Conversion-WebUI模型构建指南

Retrieval-based-Voice-Conversion-WebUI模型构建指南

一、模型介绍 Retrieval-based-Voice-Conversion-WebUI（简称 RVC）模型是一个基于 VITS（Variational Inference with adversarial learning for end-to-end Text-to-Speech）的简单易用的语音转换框架。 具有以下特点 简单易用：RVC 模型通过简单易用的网页界面，使得用户无需深入了
阅读更多...
透彻！驯服大型语言模型（LLMs）的五种方法，及具体方法选择思路

透彻！驯服大型语言模型（LLMs）的五种方法，及具体方法选择思路

引言 随着时间的发展，大型语言模型不再停留在演示阶段而是逐步面向生产系统的应用，随着人们期望的不断增加，目标也发生了巨大的变化。在短短的几个月的时间里，人们对大模型的认识已经从对其zero-shot能力感到惊讶，转变为考虑改进模型质量、提高模型可用性。 「大语言模型(LLMs)其实就是利用高容量的模型架构（例如Transformer）对海量的、多种多样的数据分布进行建模得到，它包含了大量的先验
阅读更多...
图神经网络模型介绍（1）

图神经网络模型介绍（1）

我们将图神经网络分为基于谱域的模型和基于空域的模型，并按照发展顺序详解每个类别中的重要模型。 1.1基于谱域的图神经网络         谱域上的图卷积在图学习迈向深度学习的发展历程中起到了关键的作用。本节主要介绍三个具有代表性的谱域图神经网络：谱图卷积网络、切比雪夫网络和图卷积网络。 （1）谱图卷积网络 卷积定理：函数卷积的傅里叶变换是函数傅里叶变换的乘积，即F{f*g}
阅读更多...
秋招最新大模型算法面试，熬夜都要肝完它

秋招最新大模型算法面试，熬夜都要肝完它

💥大家在面试大模型LLM这个板块的时候，不知道面试完会不会复盘、总结，做笔记的习惯，这份大模型算法岗面试八股笔记也帮助不少人拿到过offer ✨对于面试大模型算法工程师会有一定的帮助，都附有完整答案，熬夜也要看完，祝大家一臂之力 这份《大模型算法工程师面试题》已经上传CSDN，还有完整版的大模型 AI 学习资料，朋友们如果需要可以微信扫描下方CSDN官方认证二维码免费领取【保证100%免费
阅读更多...
【生成模型系列（初级）】嵌入（Embedding）方程——自然语言处理的数学灵魂【通俗理解】

【生成模型系列（初级）】嵌入（Embedding）方程——自然语言处理的数学灵魂【通俗理解】

【通俗理解】嵌入（Embedding）方程——自然语言处理的数学灵魂 关键词提炼 #嵌入方程 #自然语言处理 #词向量 #机器学习 #神经网络 #向量空间模型 #Siri #Google翻译 #AlexNet 第一节：嵌入方程的类比与核心概念【尽可能通俗】 嵌入方程可以被看作是自然语言处理中的“翻译机”，它将文本中的单词或短语转换成计算机能够理解的数学形式，即向量。 正如翻译机将一种语言
阅读更多...
AI Toolkit + H100 GPU，一小时内微调最新热门文生图模型 FLUX

AI Toolkit + H100 GPU，一小时内微调最新热门文生图模型 FLUX

上个月，FLUX 席卷了互联网，这并非没有原因。他们声称优于 DALLE 3、Ideogram 和 Stable Diffusion 3 等模型，而这一点已被证明是有依据的。随着越来越多的流行图像生成工具（如 Stable Diffusion Web UI Forge 和 ComyUI）开始支持这些模型，FLUX 在 Stable Diffusion 领域的扩展将会持续下去。 自 FLU
阅读更多...
SWAP作物生长模型安装教程、数据制备、敏感性分析、气候变化影响、R模型敏感性分析与贝叶斯优化、Fortran源代码分析、气候数据降尺度与变化影响分析

SWAP作物生长模型安装教程、数据制备、敏感性分析、气候变化影响、R模型敏感性分析与贝叶斯优化、Fortran源代码分析、气候数据降尺度与变化影响分析

查看原文>>>全流程SWAP农业模型数据制备、敏感性分析及气候变化影响实践技术应用 SWAP模型是由荷兰瓦赫宁根大学开发的先进农作物模型，它综合考虑了土壤-水分-大气以及植被间的相互作用；是一种描述作物生长过程的一种机理性作物生长模型。它不但运用Richard方程，使其能够精确的模拟土壤中水分的运动，而且耦合了WOFOST作物模型使作物的生长描述更为科学。 本文让更多的科研人员和农业工作者
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2