MATLAB - 计算机械臂关节扭矩以平衡末端力和力矩

本文主要是介绍MATLAB - 计算机械臂关节扭矩以平衡末端力和力矩，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

系列文章目录

前言

产生力矩以平衡作用在平面机器人末端执行器体上的端点力。要使用各种方法计算关节力矩，请使用刚体树机器人模型的几何雅各比（geometricJacobian）和反动力学（inverseDynamics）对象函数。

一、初始化机器人

双关节刚体树机器人是一个二维平面机器人。关节配置以列向量形式输出。

twoJointRobot = twoJointRigidBodyTree("column");

二、问题设置

端点力 eeForce 是一个列向量，包含作用在末端执行器本体（"工具"）上的线性力和力矩的组合。请注意，该矢量以基本坐标系表示，如下图所示。

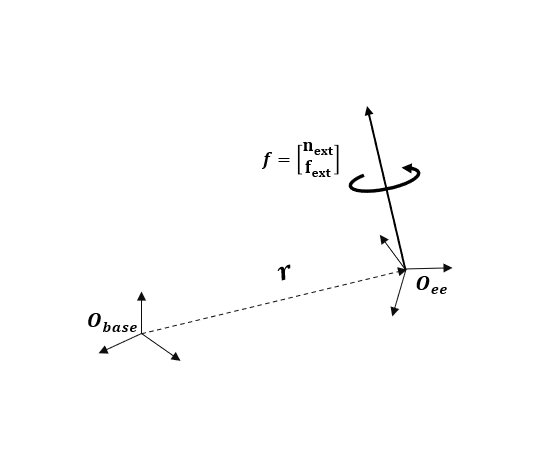
fx = 2; 
fy = 2;
fz = 0;
nx = 0;
ny = 0;
nz = 3;
eeForce = [nx;ny;nz;fx;fy;fz];
eeName = "tool";

为平衡扭矩指定机器人的关节配置。

q = [pi/3;pi/4];
Tee = getTransform(twoJointRobot,q,eeName);

三、几何雅各布法

利用虚功原理 [1]，使用几何雅各宾函数并将雅各宾的转置与端点力矢量相乘，即可求得平衡力矩。

J = geometricJacobian(twoJointRobot,q,eeName);
jointTorques = J' * eeForce;
fprintf("Joint torques using geometric Jacobian (Nm): [%.3g, %.3g]",jointTorques);

Joint torques using geometric Jacobian (Nm): [1.41, 1.78]

四、空间变换力的反动力学计算

使用另一种方法，计算平衡力矩，方法是计算将端点力空间转换到基准坐标系的反动力学。

将扭矩从末端执行器坐标系空间变换到基准坐标系，意味着在一个恰好与基准坐标系空间重合的坐标系中施加一个新的扭矩，但该坐标系仍固定在末端执行器本体上；这个新的扭矩与在 ee 原点施加的原始扭矩具有相同的效果。下图中， $f_{ext}$ 和 $n_{ext}$ 分别为端点线性力和力矩， $\mathbf{f}_\mathbf{ee}^{\mathbf{base}}$ 和 $\mathbf{n}_\mathbf{ee}^{\mathbf{base}}$ 分别为空间变换后的力和力矩。在下面的片段中， $\mathbf{f}_\mathbf{ee}^{\mathbf{base}}$ 是空间变换后的扭矩。

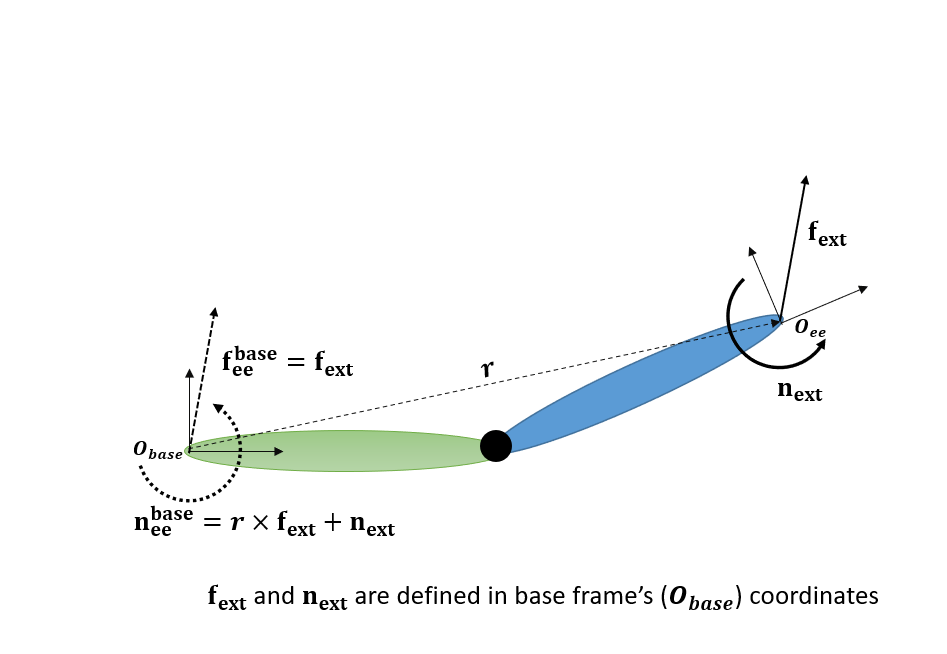
r = tform2trvec(Tee);
fbase_ee = [cross(r,[fx fy fz])' + [nx;ny;nz]; fx;fy;fz];
fext = -externalForce(twoJointRobot, eeName, fbase_ee);
jointTorques2 = inverseDynamics(twoJointRobot, q, [], [], fext);
fprintf("Joint torques using inverse dynamics (Nm): [%.3g, %.3g]",jointTorques2)

Joint torques using inverse dynamics (Nm): [1.41, 1.78]

五、末端执行器力的反动力学

使用第三种方法，将末端执行器力表示在其自身坐标系（fee_ee）中，而不是将末端执行器力进行空间变换到基础坐标系。将力矩和线性力向量转换到末端执行器坐标系中。然后，将该力和当前配置指定给 externalForce 函数。根据该力矢量计算逆动力学。

eeLinearForce = Tee \ [fx;fy;fz;0];
eeMoment = Tee \ [nx;ny;nz;0];
fee_ee = [eeMoment(1:3); eeLinearForce(1:3)];
fext = -externalForce(twoJointRobot,eeName,fee_ee,q);
jointTorques3 = inverseDynamics(twoJointRobot, q, [], [], fext);
fprintf("Joint torques using inverse dynamics (Nm): [%.3g, %.3g]",jointTorques3);

Joint torques using inverse dynamics (Nm): [1.41, 1.78]

参考资料

[1]Siciliano, B., Sciavicco, L., Villani, L., & Oriolo, G. (2009). Differential kinematics and statics. Robotics: Modelling, Planning and Control, 105-160.

[2]Harry Asada, and John Leonard. 2.12 Introduction to Robotics. Fall 2005. Chapter 6 Massachusetts Institute of Technology: MIT OpenCourseWare, https://ocw.mit.edu. License: Creative Commons BY-NC-SA.

这篇关于MATLAB - 计算机械臂关节扭矩以平衡末端力和力矩的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！